R语言对正交实验结果（含交互作用）进行极差分析与方差分析实例

题目

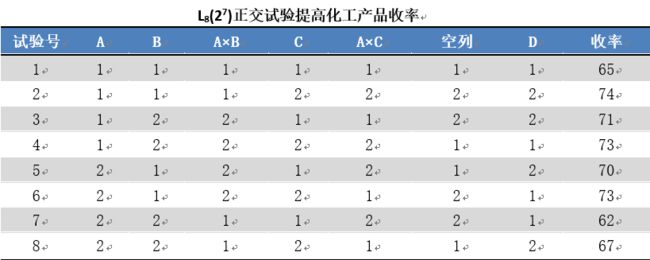
某工厂为了提高某产品的收率，根据经验和分析，认为反应温度A、反应时间B、碱用量C和催化剂种类D可能对产品的收率造成较大的影响,并考虑交互作用AB，AC。用正交表L8(27)安排试验，试验方案及结果如下表所示，试用直观分析和方差分析来分析结果。

解答

1 数据预处理

读取数据，对各因子列数据进行因子化处理，并将最后一列y对应值赋值给response

mydata = read.csv("data2.csv",fileEncoding = "UTF-8-BOM")
head(mydata)

attach(mydata)
for (i in 3:ncol(mydata)-1) {
  mydata[,i] <- as.factor(mydata[,i])
}

response = mydata[,ncol(mydata)]

> mydata = read.csv("data2.csv",fileEncoding = "UTF-8-BOM")
> head(mydata)
  试验号 A B A.B C A.C 空列 D 收率
1      1 1 1   1 1   1    1 1   65
2      2 1 1   1 2   2    2 2   74
3      3 1 2   2 1   1    2 2   71
4      4 1 2   2 2   2    1 1   73
5      5 2 1   2 1   2    1 2   70
6      6 2 1   2 2   1    2 1   73
> 
> #attach(mydata)
> for (i in 3:ncol(mydata)-1) {
+   mydata[,i] <- as.factor(mydata[,i])
+ }
> 
> response = mydata[,ncol(mydata)]
> 

2 直观分析法

分别计算每一个因子对应的极差（各水平下最大均值-最小均值），将计算结果存于数据框K中

k.max = c(NULL)#存最大效应值
k.min = c(NULL)#存最小效应值
k.maxlevel = c(NULL)#最大效应值对应水平
J = 1
for (i in 3:ncol(mydata)-1) {
  KK = tapply(response, mydata[,i], mean)
  k.max[J] = each(max)(KK)
  k.min[J] = each(min)(KK)
  k.maxlevel[J] = which(KK==k.max[J])
  J=J+1
}
k.mean = k.max - k.min#计算极差
factors = colnames(mydata)[3:ncol(mydata)-1]
K <- data.frame(factors,k.mean, k.maxlevel, k.max, k.min) ##生成数据框
K

> k.max = c(NULL)#存最大效应值
> k.min = c(NULL)#存最小效应值
> k.maxlevel = c(NULL)#最大效应值对应水平
> J = 1
> for (i in 3:ncol(mydata)-1) {
+   KK = tapply(response, mydata[,i], mean)
+   k.max[J] = each(max)(KK)
+   k.min[J] = each(min)(KK)
+   k.maxlevel[J] = which(KK==k.max[J])
+   J=J+1
+ }
> k.mean = k.max - k.min#计算极差
> factors = colnames(mydata)[3:ncol(mydata)-1]
> K <- data.frame(factors,k.mean, k.maxlevel, k.max, k.min) ##生成数据框
> K
  factors k.mean k.maxlevel k.max k.min
1       A   2.75          1 70.75 68.00
2       B   2.25          1 70.50 68.25
3     A.B   4.75          2 71.75 67.00
4       C   4.75          2 71.75 67.00
5     A.C   0.75          2 69.75 69.00
6    空列   1.25          2 70.00 68.75
7       D   2.25          2 70.50 68.25
>

由计算结果可知，若只考虑极差的效果，则各因素对响应值的效应主次排序为：
$$C=A\times B>A>B=D>空列>A\times C$$
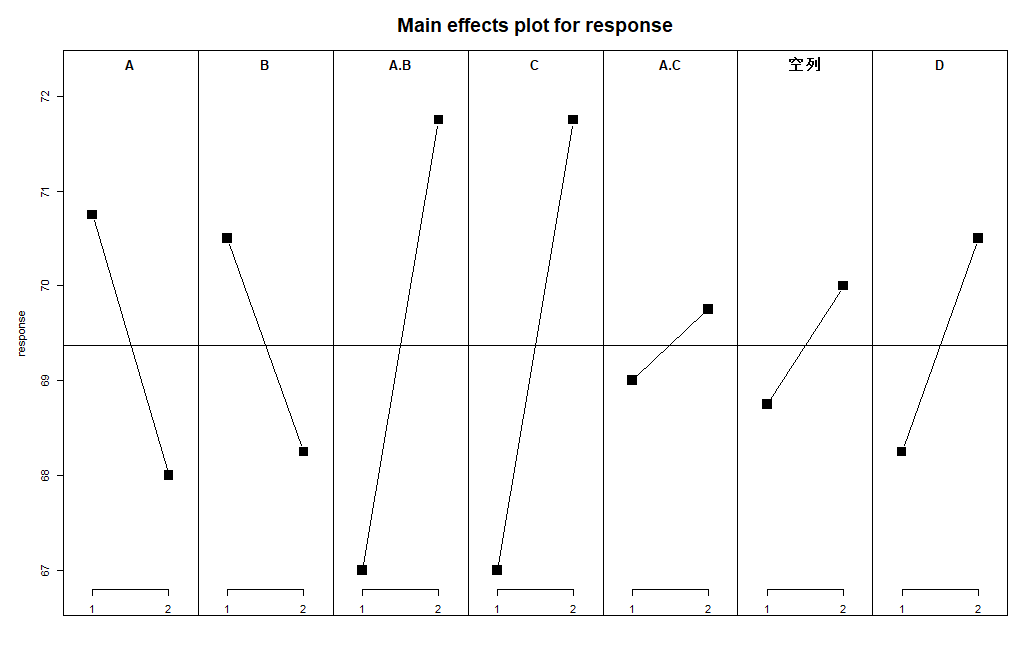
绘制因子各水平作用效应均值图：

#只有当正交实验中各因子为两水平时才可以调用以下代码绘制图形
library(DoE.base)
library(FrF2)
lm.model = lm(response~A+B+A.B+C+A.C+空列+D,data=mydata)
MEPlot(lm.model, abbrev = 2, response = "mean")

其中AXC的效应比误差列还小，故不太显著；其它因素的效应较大，认为比较显著

最大收率对应的最优组合为：$C_2{A}_1{B}_2{D}_2$

3 方差分析法

3.1 正态性检验

对全体响应(response)进行正态性分布，采用w检验

shapiro.test(response)#检验全体response

> shapiro.test(response)

	Shapiro-Wilk normality test

data:  response
W = 0.91452, p-value = 0.387

检验原假设是全体响应满足正态性分布，由w检验可知$p>0.05$，接受原假设，response服从正态分布

3.2 方差齐性检验

采用bartlett方法对各因子不同水平下响应进行方差齐性检验

bartlett.test(response ~ A, data = mydata)
bartlett.test(response ~ B, data = mydata)
bartlett.test(response ~ A.B, data = mydata)
bartlett.test(response ~ C, data = mydata)
bartlett.test(response ~ A.C, data = mydata)
bartlett.test(response ~ 空列, data = mydata)
bartlett.test(response ~ D, data = mydata)

> bartlett.test(response ~ A, data = mydata)

	Bartlett test of homogeneity of variances

data:  response by A
Bartlett's K-squared = 0.058776, df = 1, p-value = 0.8084

> bartlett.test(response ~ B, data = mydata)

	Bartlett test of homogeneity of variances

data:  response by B
Bartlett's K-squared = 0.086259, df = 1, p-value = 0.769

> bartlett.test(response ~ A.B, data = mydata)

	Bartlett test of homogeneity of variances

data:  response by A.B
Bartlett's K-squared = 3.1548, df = 1, p-value = 0.0757

> bartlett.test(response ~ C, data = mydata)

	Bartlett test of homogeneity of variances

data:  response by C
Bartlett's K-squared = 0.2012, df = 1, p-value = 0.6538

> bartlett.test(response ~ A.C, data = mydata)

	Bartlett test of homogeneity of variances

data:  response by A.C
Bartlett's K-squared = 0.39792, df = 1, p-value = 0.5282

> bartlett.test(response ~ 空列, data = mydata)

	Bartlett test of homogeneity of variances

data:  response by 空列
Bartlett's K-squared = 0.49935, df = 1, p-value = 0.4798

> bartlett.test(response ~ D, data = mydata)

	Bartlett test of homogeneity of variances

data:  response by D
Bartlett's K-squared = 1.0656, df = 1, p-value = 0.3019

由检验结果可知，各因子不同水平下检验方差齐性时原假设发生概率 $p>0.05$均成立，故接受原假设，各因子不同水平下的各组响应满足方差齐性

3.3 方差分析

使用aov()函数对数据进行方差分析;检验对象为响应(response),先计算4各因子所对应的方差

first_aov = aov(response~A+B+A.B+C+A.C+空列+D,data=mydata)
summary(first_aov)

> first_aov = aov(response~A+B+A.B+C+A.C+空列+D,data=mydata)
> summary(first_aov)
            Df Sum Sq Mean Sq
A            1  15.13   15.13
B            1  10.12   10.12
A.B          1  45.12   45.12
C            1  45.13   45.13
A.C          1   1.13    1.13
空列         1   3.13    3.13
D            1  10.13   10.13

由方差计算结果可知，
$$V_{A.C}=1.13,V_{空列}=3.13，V_{A.C}<V_{空列}$$
由此认为在$V_{A.C}$的偏差中，由因素水平变化的影响部分很小，它的偏差实际上主要是由于误差干扰造成的，这在进行显著性实验前就能确定。因此将$S_{A.C},S_{空列}$合并在一起，用于估计误差影响的大小，而且误差的自由度越大，进行显著性检验时越精确

3.4 显著性检验

合并后，对余下各列进行显著性检验

last_aov = aov(response ~ A+B+A.B+C+D,data=mydata)
summary(last_aov)

> last_aov = aov(response ~ A+B+A.B+C+D,data=mydata)
> summary(last_aov)
            Df Sum Sq Mean Sq F value Pr(>F)  
A            1  15.13   15.13   7.118  0.116  
B            1  10.12   10.12   4.765  0.161  
A.B          1  45.12   45.12  21.235  0.044 *
C            1  45.13   45.13  21.235  0.044 *
D            1  10.13   10.13   4.765  0.161  
Residuals    2   4.25    2.13                 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> 

由显著性检验结果可知，对于原假设H0：因素C对收率无显著影响，而方差分析结果为原假设出现的概率 $p=0.044，p<0.05$，故认为不同C对收率有显著影响。同理可知，AXB（A与B的交互作用）有显著影响，而B、D和AXC对收率无显著影响。

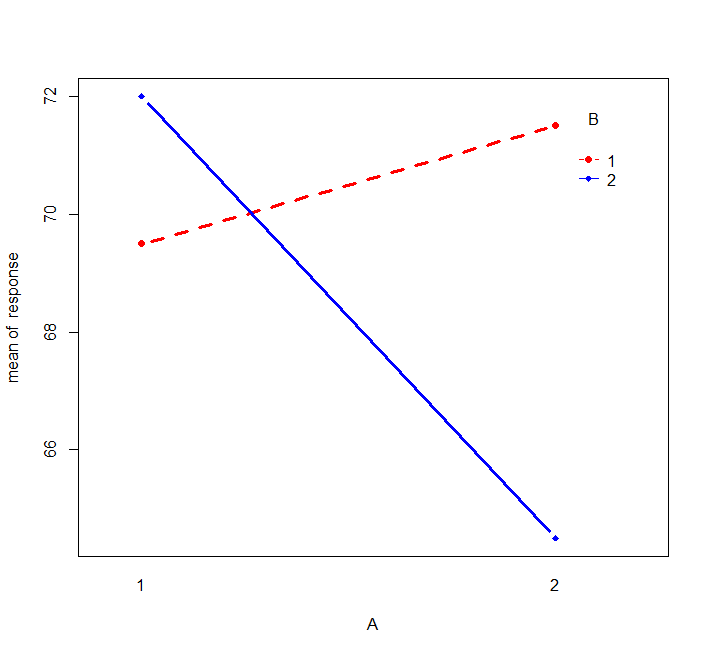
绘制A与B的交互作用图进行辅助说明

with(mydata,interaction.plot(A,B,response,col=c("red","blue"),pch=c(16,18),type="b",lwd=3))

交互作用图中,两线交叉进一步证明AB间存在有交互作用。

4 结论

结合直观分析法和方差分析法，可知

• A的效应比随机误差带来的明显，但不显著；

• B的效应比随机误差带来的明显，但不显著；

• AXB（AB间的交互作用）对收率影响显著；

• C对收率影响显著；

• D的效应比随机误差带来的明显，但不显著；

• AXC（AC间的交互作用）的效应比随机误差带来的还要弱，不显著

最大收率对应的最优组合为：$C_2{A}_1{B}_2{D}_2,即A_1{B}_2{C}_2{D}_2$