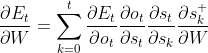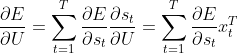RNN循环神经网络

入门小菜鸟，希望像做笔记记录自己学的东西，也希望能帮助到同样入门的人，更希望大佬们帮忙纠错啦~侵权立删。

✨完整代码在我的github上，有需要的朋友可以康康✨

​​​​​​https://github.com/tt-s-t/Deep-Learning.git

目录

一、RNN出现的意义

二、引入 —— 语言模型

1、语言模型是什么

2、语言模型的计算

3、n元语法

三、RNN原理

1、RNN模型结构和前向传播

 2、反向传播

3、反向传播的问题所在

4、裁剪梯度

5、注意点

四、RNN的应用以及不足

1、RNN应用领域

2、不足

五、RNN代码实现

1、初始化参数

2、前向传播

3、反向传播

4、预测

5、定义数据处理类

6、完整调用

7、结果

---

一、RNN出现的意义

我们所熟悉的CNN，它的输出都是只考虑前一个输入的影响而不考虑其它时刻输入的影响（即只能单独去处理一个又一个的输入）

但是, 对于一些与时间先后有关的, 一序列的信息（即前后输入是有关系的），比如进行文档前后文内容的预测等等, 这时候CNN的效果就不太好了。

而我们人的认知是基于过往的经验和记忆的，以此观点和对上述CNN不足的弥补，设计了不仅考虑前一时刻的输入,还能记忆网络前面的内容的循环神经网络——RNN。

---

二、引入 —— 语言模型

1、语言模型是什么

我们把一段自然语言文本看作是一段离散的时间序列。

假设一段长度为T的文本，其中的词依次为：。其中  是时间步 t 的输出/标签。

那么语言模型将计算该序列的概率：；以概率最大的序列作为语言模型的输出。

2、语言模型的计算

这些概率则由该词在训练集中的相对词频计算出来。

3、n元语法

当序列长度增加时，需要计算和存储的概率的复杂度会呈指数级增加。

为了解决这个问题，n元语法应运而生。

n元语法是基于n-1阶马尔可夫链的概率语言模型，这是指一个词的出现只与前面n-1个词相关。

存在问题：

当n较小的时候，n元语法不准确；较大时，n元语法需要计算和存储大量相关概率。

---

三、RNN原理

1、RNN模型结构和前向传播

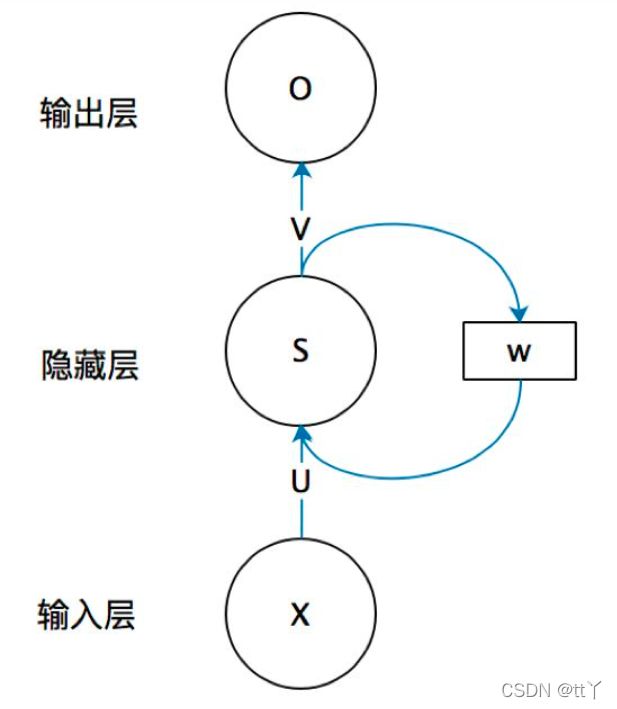
RNN由输入层，隐藏层和输出层组成。

其中x，s，o都是向量，分别是输入层的值，隐藏层的值和输出层的值。

U是输入层到隐藏层的权重矩阵，V是隐藏层到输出层的权重矩阵，W是隐藏层上一次的值作为这一次的输入的权重矩阵。

公式如下（这里展示的是不含偏置的，含偏置的类似于全连接层那样加上去就好了）：

其中f和g是激活函数，f可以是tanh,relu,sigmoid等激活函数，而g通常是softmax。

在这里U，V，W是不变的（到反向传播再变，这里只为了强调变量是后面那3个），变的是Xt，St-1和St，这里的W*St-1就是上一时刻的值的影响（正所谓过去的记忆）加入。

简单来说：（加了偏置）

原本我们的全连接层的公式如下：（这里含一个隐藏层）

     隐藏层输出结果： 

     输出层结果：

现在加入隐藏状态（即前一时刻的“影响”）:

     隐藏层输出结果：

     输出层结果：

即前一时刻的隐藏状态。

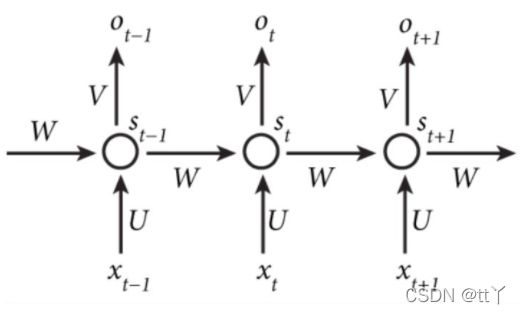
具体来说如下图所示按时间来展开

 2、反向传播

 每一次的输出值Ot都会产生一个误差值Et

而损失函数既可以使用交叉熵损失函数也可以使用平方误差损失函数

首先让我们看一下公式：

总的误差（有时为了让这个误差值小一些，常常再除以T）

参数梯度求法

由上面的公式我们可以得出他的含义：每个时刻的偏差的偏导数之和（U，V，W都是这样）

我们就以W为参照：

首先将公式用链式法则展开

然后由刚刚的式子代入，并且发现st与前面的所有时刻的s都有直接或间接的关系，可以得到下面的公式：

求

（1）当t=T时，只有一条支路：

（2）当t

总结：

因此总体式子可化为：

V和U的公式如下

3、反向传播的问题所在

当T较大或者t较小时，从指数项可得出，容易出现梯度爆炸或消失的问题。

为了应对梯度爆炸，我们可以采取裁剪梯度的方法。

4、裁剪梯度

方法一：

假设我们把所有模型参数梯度的元素拼接成一个向量g，并设裁剪阈值为，裁剪后的梯度为：

裁剪后的梯度的L2范数不超过。

方法二：

将梯度限制在一定范围内。

5、注意点

我们可以从公式中看到，许多梯度值在后续还会再次被使用，因此往往我们会存储这些梯度值，从而避免重复计算。

并且有一些值是通过正向传播计算来的，也进行存储，避免重复计算。

---

四、RNN的应用以及不足

1、RNN应用领域

自然语言处理(NLP): 主要有视频处理, 文本生成, 语言模型, 图像处理

机器翻译，文本相似度计算，图像描述生成

语音识别

推荐

2、不足

容易出现梯度消失或者梯度爆炸的问题。

原因：长时间依赖造成过拟合导致梯度爆炸以及时间过长而造成记忆值较小从而造成梯度消失。

---

五、RNN代码实现

这里只展示我用numpy搭建的RNN网络，并且实现对“abcdefg abcdefg abcdefg”序列数据的预测。详细地可以在我的github上看，包括用pytorch实现的rnn实现文本生成，以及这个numpy搭建的rnn实现对序列数据预测的完整版本。

​​​​​​https://github.com/tt-s-t/Deep-Learning.git

首先我们写一个类来实现前向传播，反向传播和最后预测。

1、初始化参数

import numpy as np
import torch.nn as nn

class RNN(object):
    def __init__(self,input_size,hidden_size):
        self.input_size = input_size
        self.hidden_size = hidden_size

        self.W_xh = np.random.randn(input_size, hidden_size)*0.01
        self.W_hh = np.random.randn(hidden_size, hidden_size)*0.01
        self.b_h = np.zeros((1, hidden_size))
        self.W_hq = np.random.randn(hidden_size, input_size)*0.01
        self.b_q = np.zeros((1, input_size))

2、前向传播

    def forward(self, inputs, h_prev): #targets是目标词的索引值(这样占的内存才会少)
        self.input = inputs
        #一次序列跑完后再更新参数
        self.hs, self.ps = {}, {} #字典形式存储
        self.hs[-1] = np.copy(h_prev) #隐藏变量赋予
        
        for t in range(len(inputs)):  
            self.hs[t] = np.tanh(np.matmul(inputs[t], self.W_xh) + np.matmul(self.hs[t-1], self.W_hh) + self.b_h) #隐藏状态 Ht. 
            ys = np.matmul(self.hs[t], self.W_hq) + self.b_q #输出
            self.ps[t] = np.exp(ys) / np.sum(np.exp(ys)) #实际输出（概率）——softmax
        return self.ps

3、反向传播

    def backward(self, targets,lr):
        
        self.loss = 0 
        dWxh, dWhh, dWhq = np.zeros_like(self.W_xh), np.zeros_like(self.W_hh), np.zeros_like(self.W_hq)
        dbh, dbq = np.zeros_like(self.b_h), np.zeros_like(self.b_q)
        dh = np.zeros_like(self.hs[0])

        T = len(self.input) - 1
        for t in reversed(range(T)): #反过来开始，因为像隐藏状态求偏导那样，越往前面分支越多
            #loss计算
            label_onehot = np.zeros_like(self.ps[t])
            label_onehot[0, targets[t]] = 1.0#第几个样本最终属于哪一类(概率为1，其他为0)
            self.loss += -np.sum(np.log(self.ps[t]) * label_onehot)

            #梯度计算
            dy = (self.ps[t] - label_onehot)
            dWhq += np.matmul(self.hs[t].T,dy)
            dbq += dy 
            dh = np.matmul(np.matmul(np.linalg.matrix_power(self.W_hh.T,T-t),self.W_hq),dy.T).T + dh 
            dh_tanh = (1 - self.hs[t] * self.hs[t]) * dh # backprop through tanh nonlinearity #tanh'(x) = 1-tanh^2(x)
            dbh += dh_tanh
            dWxh += np.matmul(self.input[t].T.reshape(-1,1), dh_tanh)
            dWhh += np.matmul(dh_tanh, self.hs[t-1].T)

        #梯度裁剪(这里的限制范围需要自己根据需求调整，否则梯度太大会很难很难训练，loss会降不下去的)
        for dparam in [dWxh, dWhh, dWhq, dbh, dbq]: 
            np.clip(dparam, -0.5, 0.5, out=dparam)#限制在[-0.5,0.5]之间

        #参数更新
        self.W_xh += -lr * dWxh
        self.W_hh += -lr * dWhh
        self.W_hq += -lr * dWhq
        self.b_h += -lr * dbh
        self.b_q += -lr * dbq
        
        return self.loss

4、预测

    def pre(self,input_onehot,h_prev,next_len,vocab): #input_onehot为输入的一个词的onehot编码，next_len为需要生成的单词长度，vocab是"索引-词"的词典
        xs, hs = {}, {} #字典形式存储
        hs[-1] = np.copy(h_prev) #隐藏变量赋予
        xs[0] = input_onehot
        pre_vocab = []
        for t in range(next_len):
            hs[t] = np.tanh(np.matmul(xs[t], self.W_xh) + np.matmul(hs[t-1], self.W_hh) + self.b_h) #隐藏状态 Ht. 
            ys = np.matmul(hs[t], self.W_hq) + self.b_q #输出
            ps = np.exp(ys) / np.sum(np.exp(ys))
            pre_vocab.append(vocab[np.argmax(ps)])
            xs[t+1] = np.zeros((1, self.input_size)) # init
            xs[t+1][0,np.argmax(ps)] = 1
        return pre_vocab

5、定义数据处理类

from rnn_model import RNN
import numpy as np
import math

class Dataset(object):
    def __init__(self,txt_data, sequence_length):
        self.txt_len = len(txt_data) #文本长度
        vocab = list(set(txt_data)) #所有字符合集
        self.n_vocab = len(vocab) #字典长度
        self.sequence_length = sequence_length
        self.vocab_to_index = dict((c, i) for i, c in enumerate(vocab)) #词-索引字典
        self.index_to_vocab = dict((i, c) for i, c in enumerate(vocab)) #索引-词字典
        self.txt_index = [self.vocab_to_index[i] for i in txt_data] #输入文本的索引表示

    def one_hot(self,input):
        onehot_encoded = []
        for i in input:
            letter = [0 for _ in range(self.n_vocab)] 
            letter[i] = 1
            onehot_encoded.append(letter)
        onehot_encoded = np.array(onehot_encoded)
        return onehot_encoded
    
    def __getitem__(self, index):
        return (
            self.txt_index[index:index+self.sequence_length],
            self.txt_index[index+1:index+self.sequence_length+1]
        )

6、完整调用

#输入的有规律的序列数据
txt_data = "abcdefg abcdefg abcdefg abcdefg abcdefg abcdefg abcdefg abcdefg abcdefg abcdefg abcdefg abcdefg"

#config
max_epoch = 500
sequence_length = 10
dataset = Dataset(txt_data,sequence_length)
batch_size = math.ceil(dataset.txt_len /sequence_length) #向上取整
hidden_size = 100  
lr = 0.01

model = RNN(dataset.n_vocab,hidden_size)

#训练
for epoch in range(max_epoch):
    h_prev = np.zeros((1, hidden_size))
    loss = 0
    for b in range(batch_size):
        (x,y) = dataset[b]
        input = dataset.one_hot(x)
        ps = model.forward(input,h_prev) #注意：每个batch的h都是从0初始化开始，batch与batch间的隐藏状态没有关系
        loss += model.backward(y,lr)
    print(loss/batch_size)

#预测
input_txt = 'a'
input_onehot = dataset.one_hot([dataset.vocab_to_index[input_txt]])
next_len = 50 #预测后几个word
h_prev = np.zeros((1, hidden_size))
pre_vocab = ['a']
pre_vocab1 = model.pre(input_onehot,h_prev,next_len,dataset.index_to_vocab)
pre_vocab = pre_vocab + pre_vocab1
print(''.join(pre_vocab))

7、结果

 emmm预测得还不错

---

欢迎大家在评论区批评指正，谢谢~