RANSAC算法（原理及代码实现+迭代次数参数自适应）

前言

  随机样本一致性 (RANSAC) 是一种迭代方法，用于从一组包含异常值的观察数据中估计数学模型的参数，此时异常值不会对估计值产生影响。简言之，RANSAC是一种滤除异常值的常用算法。

算法流程

  以直线拟合为例，通用RANSAC算法的流程如下

输入:
    data – 观测结果.
    model – 数学模型.
    n – 估计模型所需的最小样本.
    k – 最大迭代次数.
    t – 用于确定模型适合的数据点的阈值.


输出:
    bestFit – 模型

iterations = 0
bestFit = null
bestErr = something really large

while iterations < k do
    maybeInliers := n randomly selected values from data
    maybeModel := model parameters fitted to maybeInliers
    alsoInliers := empty set
    for every point in data not in maybeInliers do
        if point fits maybeModel with an error smaller than t
             add point to alsoInliers
        end if
    end for
    if the number of elements in alsoInliers is > d then
        betterModel := model parameters fitted to all points in maybeInliers and alsoInliers
        thisErr := a measure of how well betterModel fits these points
        if thisErr < bestErr then
            bestFit := betterModel
            bestErr := thisErr
        end if
    end if
    increment iterations
end while

return bestFit

Python代码

"""_summary_
RANSAC直线拟合
"""
from copy import copy
import numpy as np
from numpy.random import default_rng
rng = default_rng()

class RANSAC:
    def __init__(self, n=10, k=100, t=0.05, d=10, model=None, loss=None, metric=None):
        self.n = n              
        self.k = k              
        self.t = t              
        self.d = d              
        self.model = model     
        self.loss = loss        
        self.metric = metric  
        self.best_fit = None
        self.best_error = np.inf

    def fit(self, X, y):

        for _ in range(self.k):
            ids = rng.permutation(X.shape[0])

            maybe_inliers = ids[: self.n]
            maybe_model = copy(self.model).fit(X[maybe_inliers], y[maybe_inliers])

            thresholded = (
                self.loss(y[ids][self.n :], maybe_model.predict(X[ids][self.n :]))
                < self.t
            )

            inlier_ids = ids[self.n :][np.flatnonzero(thresholded).flatten()]

            if inlier_ids.size > self.d:
                inlier_points = np.hstack([maybe_inliers, inlier_ids])
                better_model = copy(self.model).fit(X[inlier_points], y[inlier_points])

                this_error = self.metric(
                    y[inlier_points], better_model.predict(X[inlier_points])
                )

                if this_error < self.best_error:
                    self.best_error = this_error
                    self.best_fit = maybe_model

        return self

    def predict(self, X):
        return self.best_fit.predict(X)


def square_error_loss(y_true, y_pred):
    return (y_true - y_pred) ** 2

def mean_square_error(y_true, y_pred):
    return np.sum(square_error_loss(y_true, y_pred)) / y_true.shape[0]

class LinearRegressor:
    def __init__(self):
        self.params = None

    def fit(self, X: np.ndarray, y: np.ndarray):
        r, _ = X.shape
        X = np.hstack([np.ones((r, 1)), X])
        self.params = np.linalg.inv(X.T @ X) @ X.T @ y
        return self

    def predict(self, X: np.ndarray):
        r, _ = X.shape
        X = np.hstack([np.ones((r, 1)), X])
        return X @ self.params

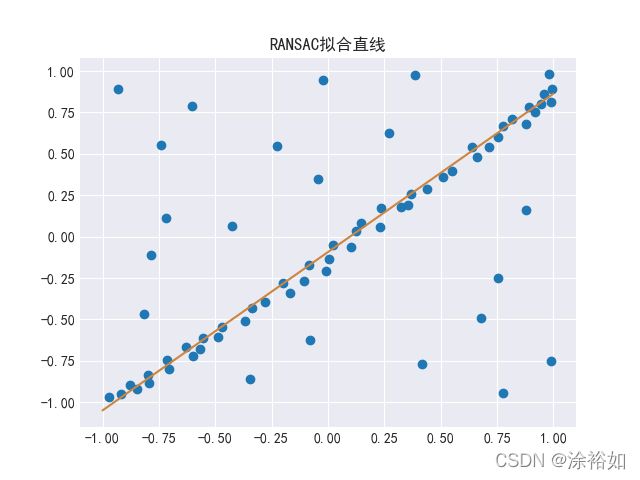
if __name__ == "__main__":

    regressor = RANSAC(model=LinearRegressor(), loss=square_error_loss, metric=mean_square_error)

    X = np.array([-0.848,-0.800,-0.704,-0.632,-0.488,-0.472,-0.368,-0.336,-0.280,-0.200,-0.00800,-0.0840,0.0240,0.100,0.124,0.148,0.232,0.236,0.324,0.356,0.368,0.440,0.512,0.548,0.660,0.640,0.712,0.752,0.776,0.880,0.920,0.944,-0.108,-0.168,-0.720,-0.784,-0.224,-0.604,-0.740,-0.0440,0.388,-0.0200,0.752,0.416,-0.0800,-0.348,0.988,0.776,0.680,0.880,-0.816,-0.424,-0.932,0.272,-0.556,-0.568,-0.600,-0.716,-0.796,-0.880,-0.972,-0.916,0.816,0.892,0.956,0.980,0.988,0.992,0.00400]).reshape(-1,1)
    y = np.array([-0.917,-0.833,-0.801,-0.665,-0.605,-0.545,-0.509,-0.433,-0.397,-0.281,-0.205,-0.169,-0.0531,-0.0651,0.0349,0.0829,0.0589,0.175,0.179,0.191,0.259,0.287,0.359,0.395,0.483,0.539,0.543,0.603,0.667,0.679,0.751,0.803,-0.265,-0.341,0.111,-0.113,0.547,0.791,0.551,0.347,0.975,0.943,-0.249,-0.769,-0.625,-0.861,-0.749,-0.945,-0.493,0.163,-0.469,0.0669,0.891,0.623,-0.609,-0.677,-0.721,-0.745,-0.885,-0.897,-0.969,-0.949,0.707,0.783,0.859,0.979,0.811,0.891,-0.137]).reshape(-1,1)

    regressor.fit(X, y)

    import matplotlib.pyplot as plt
    plt.style.use("seaborn-darkgrid")
    fig, ax = plt.subplots(1, 1)
    # 支持中文
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

    plt.scatter(X, y)
    plt.title("RANSAC拟合直线")
    line = np.linspace(-1, 1, num=100).reshape(-1, 1)
    plt.plot(line, regressor.predict(line), c="peru")
    plt.show()

RANSAC算法迭代参数的自适应

  上面提到的RANSAC算法总要迭代足够的次数才能终止，这就留给设计者一个难题，迭代次数少了，找不到最优解，迭代次数多了，程序耗时增加。接下来给读者介绍一种自适应的迭代次数的方法。
  当错误点所占比例较小时，则应该尽快停止迭代；反之，则需要足够的迭代次数再终止算法以获取更可靠的结果。
  令 $p:$ :RANSAC 算法在运行后提供至少一个有用结果的期望概率。
  令$w:$ 满足模型的点 / 检测到的所有点
  令$n:$满足当前模型的点的个数
  则$1-p=(1-w^n{)}^k$
  即$k=\frac{log(1-p)}{log(1-w^n)}$
  代码实现过程如下

// 以下代码来自OpenCV
/**
 * @Method:    更新ransac的迭代次数
 * @Returns:   int 更新后的最大迭代次数
 * @Qualifier: 
 * @Parameter: double p 信心分数
 * @Parameter: double ep 错误点所占的比例
 * @Parameter: int modelPoints 模型中点的数量
 * @Parameter: int maxIters 当前最大迭代次数
 */
int RANSACUpdateNumIters( double p, double ep, int modelPoints, int maxIters )
{
    if( modelPoints <= 0 )
        CV_Error( Error::StsOutOfRange, "the number of model points should be positive" );

    p = MAX(p, 0.);
    p = MIN(p, 1.);
    ep = MAX(ep, 0.);
    ep = MIN(ep, 1.);

    // avoid inf's & nan's
    double num = MAX(1. - p, DBL_MIN);
    double denom = 1. - std::pow(1. - ep, modelPoints);
    if( denom < DBL_MIN )
        return 0;

    num = std::log(num);
    denom = std::log(denom);

    return denom >= 0 || -num >= maxIters*(-denom) ? maxIters : cvRound(num/denom);
}