人工智能学习（五）：约束满足问题（上）

目录

引言

6.1 定义约束满足问题

6.1.1 实例:地图着色问题

6.1.2 实例：作业调度问题

6.1.3 CSP的形式化

6.2 约束传播：CSP中的推理

6.2.1 结点相容

6.2.2 弧相容

---

引言

本篇要讨论的是如何更有效地求解更多种类的问题。使用成分表示来描述状态：即一组变量，每个变量有自己的值。当每个变量都有自己的赋值同时满足所有关于变量的约束时，问题就得到了解决。这类问题称为约束满足问题，简称CSP。

CSP搜索算法利用了状态结构的优势，使用的是通用策略而不是问题专用启发式来求解复杂问题。主要思想是通过识别违反约束的变量/值的组合迅速消除大规模的搜索空间。

6.1 定义约束满足问题

约束满足问题包含三个成分、和：

	变量集合
	值域集合，每个变量有自己的值域，值域是由变量的可能取值组成的集合
	描述变量取值的约束集合，每个约束是有序对，其中是约束中的变量组，则定义了这些变量取值应满足的关系

关系可以显式地列出所有关系元组，也可以是支持如下两个操作的抽象关系：测试一个元组是否为一个关系的成员和枚举所有关系成员。

例如，如果、的值域均为，约束是二者不能取相同值，关系可如下描述:或。

为求解CSP,需要定义状态空间和解的概念。问题的状态由对部分或全部变量的一个赋值来定义，。一个不违反任何约束条件的赋值称作相容的或者合法的赋值。完整赋值是指每个变量都已赋值，而CSP的解是相容的、完整的赋值。部分赋值是指只有部分变量赋值。

6.1.1 实例:地图着色问题

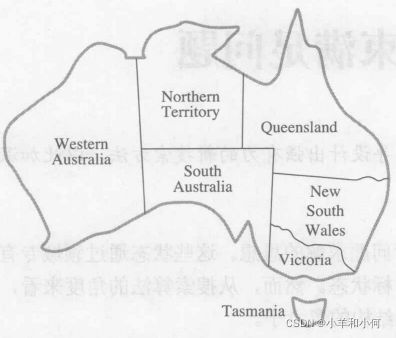
现在来看澳大利亚地图，地图显示出每个州及边界。任务是对每个区域涂上红色、绿色或者蓝色，要求是相邻的区域颜色不能相同。将此任务形式化为CSP,把图中的区域定义为变量：

可以枚举如下：

这个问题有很多可能的解，如：

把CSP可视化地表示为下图所示的约束图很有用。图中结点对应于问题的变量，变量间的连线表示两者之间有约束。

为什么要把问题形式化成CSP呢？

1. 用CSP表示各种问题很自然：如果你有CSP求解系统，使用它求解问题，比用其他搜索技术来求解要简单得多。
2. CSP求解比状态空间搜索要快，因为CSP求解能快速消除庞大的搜索空间。例如，在澳大利亚问题中一且选择，立刻得出它的5个邻居都不能取值。不考虑约束传播，搜索过程需要考虑5个邻居变量的种赋值组合;有了约束传播就不用再考虑赋值为的情况，赋值组合为，减少了。

在常规的状态空间搜索中我们只能一个一个状态的问：这个状态是目标吗？有了CSP，一旦发现某部分赋值不会是解，可立刻丢弃不会再做进一步求精。更进一步，可以看出为什么某赋值不是解可以看出是哪个变量违反了约束——这样可以集中关注发生影响的变量。所以，许多不能用常规状态空间搜索求解的棘手问题可以很快地用CSP解决。

6.1.2 实例：作业调度问题

考虑一小部分汽车组装，包括15个任务：安装轮轴（前和后），安装四个车轮（前后左右），拧紧每个车轮的螺母，安装轮毂罩和检查完整安装。 可用15个变量表示：

变量的值是任务的开始时间。下面引入任务间的过程约束。任务，必须在任务前完成，的完成需要时间，加入如下形式的算术约束：


假设有四个工人安装车轮，但他们必须共享一个工具来帮助安放轮轴。需要析取约束来表示和在时间上不能有重合：

                

约束看起来更加复杂，既有算术约束又有逻辑约束。它减少了和同时开始的赋值组合。

还需要定义断言：检查是最后一项任务，需要3分钟。对除之外的每个变量，加入形如的约束。最后，假设整个过程只有30分钟。这样得到所有变量的值域为：

CSP很适于解决此类问题，琐碎并且约束变量可能有几千个。在一些情况下，有的约束过于复杂，很难用CSP形式化，后面会有更适合的技术。

6.1.3 CSP的形式化

最简单的CSP是指涉及的变量是离散的有限值域的。

变量的种类

离散值域

离散值域可能是无限的，如整数集合或者字符串集合。如果是无限值域，就不再可能用枚举所有可能取值的组合来描述约束条件了。就只能直接用约束语言替代，例如，不再可能通过枚举所有可能的赋值来求解。整数变量的线性约束可以求解，整数变量的非线性约束问题不可求解。

连续值域

连续值域的约束满足问题在现实世界十分常见，在运筹学领域中有很广泛的研究。例如，哈勃太空望远镜的实验日程安排要求非常精确的观测时间：每次观测的开始、结束时间和机动时间都是连续值变量，必须遵守许多天文的、优先权的和电力约束。

约束的类型

一元约束

最简单的类型是一元约束，它只限制单个变量的取值。例如，地图着色问题中可能出现这样的情况：南澳洲人不喜欢绿色；可以这样表示此一元约束。二元约束与两个变量有关。二元CSP只包含二元约束；它可以表示为约束图：

同样可以描述高阶约束，如断言Y的值处于X和Z之间，可以表示成三元约束。

全局约束

变量个数任意的约束称为全局约束（它并不一定涉及问题中的所有变量！）。最常见的全局约束是，指的是约束中的所有变量必须取不同的值。在数独游戏中，一行或一列中的所有变量必须满足约束。

另一个例子是密码算术谜题：

密码算术中每个字母都表示不同的数字。在图中，表示为六变量约束。此谜题的四列算式可表示为如下涉及多个变量的n元约束：

其中，，表示十位、百位、千位上的进位变量。这些约束可以用约束超图表示：

约束超图中包含普通结点（图中的圆圈结点）和表示n元约束的超结点（用方块表示）。

任意有限值域的约束都可以通过引入足够的约束变量而转化为二元约束，所以可以转换任何CSP成只含二元约束的；这使算法变得简单。另一种将n元CSP转换成二元CSP的方法是对偶图转换：

创建一个新图，原图中的每个约束用一个变量表示，原图中每对有同样变量的约束用一个二元约束表示。例如，如果原图中有变量和约束，对偶图中则有两个变量和二元约束，是两个约束的共有变量，为定义共有变量约束的新关系。

我们可能更喜欢诸如的全局约束而不是一组二元约束，因为：

• 使用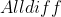描述问题更简单更不易出错。
• 对全局约束可能设计专用的推理算法。 

偏好约束

到目前为止我们描述过的约束都是绝对约束，任何违反规则的都排除在解之外。许多现实世界的CSP包含偏好约束，指出哪些解是更喜欢的。例如，在大学排课问题中有绝对约束如没有教授可以同一时间出现在不同教室。同时也有很多偏好约束：R教授可能偏好在上午授课，而N教授偏好在下午授课。R教授在下午2点授课的时间表仍是一个解，但它不是最优解。偏好约束通常被处理成个体变量赋值的开销。例如，R教授下午时段在总体目标函数中的开销是2点，而上午时段的开销只有1点。有了这样的形式化，有偏好约束的CSP可以用基于路径的或局部的最优搜索方法求解。我们称这样的问题为约束优化问题，或简写为COP。线性规划也有此类优化问题。

6.2 约束传播：CSP中的推理

在常规的状态空间搜索中，算法只能做一件事：搜索。在CSP中则有了选择：算法可以搜索（从几种可能性中选择新的变量赋值），也可以做种称为约束传播的特殊推理：使用约束来减小一个变量的合法取值范围，从而影响到跟此变量有约束关系的另一变量的取值，如此进行。约束传播与搜索可以交替进行，或者也可以把它作为搜索前的预处理步骤。有时这个预处理就可以解决整个问题，这时就完全不需要搜索了。。

核心思想是局部相容性。如果把变量看作是图中结点，约束为图中的弧，增强图中各部分局部相容性会导致不相容的结点取值被删除。局部相容性有几种，将在下面逐一讨论。

6.2.1 结点相容

如果单个变量（对应于CSP网络中的结点）值域中的所有取值满足它的一元约束，就称此变量是结点相容的。

例如，地图着色问题中南澳洲人不喜欢绿色，变量原来值域为,删除此结点即为结点相容的，此时的值域空间为。如果网络中每个变量都是结点相容的，则此网络是结点相容的。

通过运行结点相容总能消除CSP中的所有一元约束。可以将所有n元约束转换成二元的。正是因为这一点， 通常的做法是定义只含有二元约束的CSP求解器。

6.2.2 弧相容

如果CSP中某变量值域中的所有取值满足该变量的所有二元约束，则称此变量是弧相容的。

更形式地，对于变量、，若对中的每个数值在中都存在一些数值满足弧的二元约束,则称相对是弧相容的。

如果每个变量相对其他变量都是弧相容的，则称该网络是弧相容的。

例如，考虑约束，X和Y都是数字。可以显式地写出约束为：

为了使相对于是弧相容的，将的值域缩小为。如果要使相对于也是弧相容的，则的值域应缩小为，此时整个CSP就是弧相容的。

另一方面，弧相容可能对澳大利亚地图着色问题毫无帮助。考虑之间的不同色约束：
不管你如何为（或）选择取值，另一个都还有合法取值。此时应用弧相容对变量的值域没有任何影响。

最流行的弧相容算法是AC-3（应用了AC-3后，要么每条弧都是弧相容的，要么有变量的值域为空，后者说明该CSP无解）：

为使每个变量都是弧相容的，AC-3 算法维护一个弧相容队列（实际上，考虑的顺序并不重要，所以数据结构实际上是个集合，我们只是称之为队列）。首先，队列中包含CSP中的所有弧。AC-3 从队列中弹出弧，首先使相对弧相容。如果没有变化，算法则处理下一条弧。但如果发生变化（变小），那么每个指向的弧都必须重新插入队列中准备检验。之所以这么做是因为的改变可能引起的缩小，即使是在我们以前已经考虑过的情况下。如果变成了空集，我们就知道整个CSP没有相容解，AC-3 直接返回失败。否则，我们继续检查，试图缩小变量值域直到队列中没有弧。此时的CSP与原有CSP等价——它们有相同的解——但是弧相容的CSP由于变量值域更小所以求解更快。

AC-3的算法复杂度可以分析如下。假设CSP中有n个变量，变量值域最大为个元素，个二元约束（弧）。每条弧最多只能插入队列次，因为至多有个值可删除。检验一条弧的相容性可以在时间内完成，因此在最坏情况下算法的时间复杂度为。

将弧相容概念扩展成处理n元约束而不仅仅是二元约束是可能的；通常称之为通用弧相容或超弧相容。变量相对某n元约束是通用弧相容的，指的是对值域中的每个值都存在一组取值，其中的值为，其他值都在对应变量的值域中。例如，所有变量的值域为，需要使变量对约束相容，就需要从的值域中把2和3删除，因为X为2和3的时候无法满足约束。