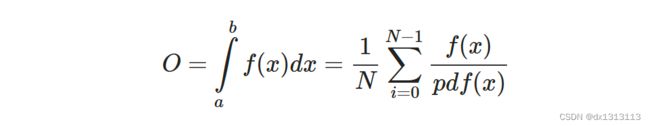蒙特卡洛积分、重要性采样、低差异序列

渲染公式

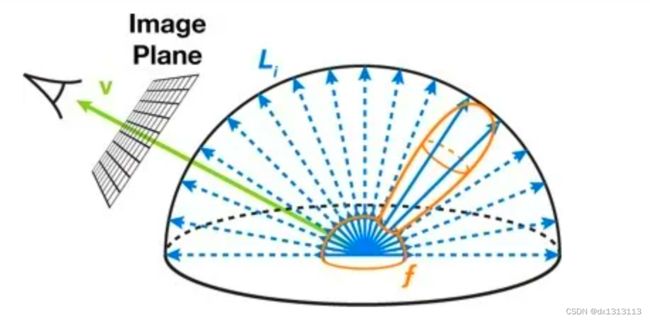
渲染的目标在于计算周围环境的光线有多少从表面像素点反射到相机视口中。要计算总的反射光，每个入射方向的贡献，必须将他们在半球上相加：

为入射光线  与法线  的夹角,为方便计算可以使用法线向量和入射向量（单位化）的乘积表示。

 对于基于图像的光照，入射光线可以由环境贴图近似，其中每个纹理像素对应一个入射方向，并忽略遮挡。但是即使采用这种近似，图像中一个像素的光照数值积分对实时渲染而言还是过于昂贵。

---

蒙特卡洛积分

蒙特卡罗积分方法是一种计算方法。原理是通过大量随机样本，去了解一个系统，进而得到所要计算的值。它非常强大和灵活，又相当简单易懂，容易实现。对于许多问题来说，它往往是最简单的计算方法，也可能是唯一方法。积分公式近似计算如下：

为了求解这个积分，我们在 a到 b上采样 N 个随机样本，将它们加在一起并除以样本总数来取平均。其中为概率分布函数，表示概率密度函数，它的含义是特定样本在整个样本集上的发生概率。

当涉及蒙特卡洛积分时，某些样本可能比其他样本具有更高的生成概率。这就是为什么对于任何一般的蒙特卡洛估计，我们都会根据 pdf 将采样值除以或乘以采样概率。到目前为止，我们每次需要估算积分的时候，生成的样本都是均匀分布的，概率完全相等。到目前为止，我们的估计是无偏的，这意味着随着样本数量的不断增加，我们最终将收敛到积分的精确解。

        但是，某些蒙特卡洛估算是有偏的，这意味着生成的样本并不是完全随机的，而是集中于特定的值或方向。这些有偏的蒙特卡洛估算具有更快的收敛速度，它们会以更快的速度收敛到精确解，但是由于其有偏性，可能永远不会收敛到精确解。通常来说，这是一个可以接受的折衷方案，尤其是在计算机图形学中。因为只要结果在视觉上可以接受，解决方案的精确性就不太重要。下文我们将会提到一种（有偏的）重要性采样，其生成的样本偏向特定的方向，在这种情况下，我们会将每个样本乘以或除以相应的 pdf 再求和。

        蒙特卡洛积分在计算机图形学中非常普遍，因为它是一种以高效的离散方式对连续的积分求近似而且非常直观的方法：对任何面积/体积进行采样——例如半球 Ω ——在该面积/体积内生成数量 NN 的随机采样，权衡每个样本对最终结果的贡献并求和。

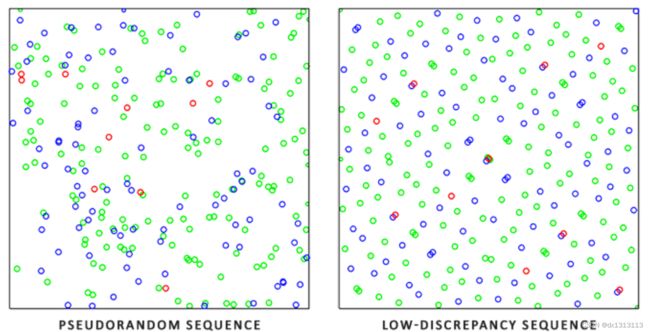
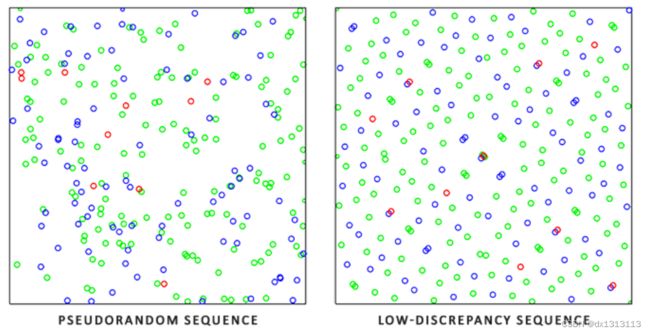
        蒙特卡洛积分是一个庞大的数学主题，在此不再赘述，但有一点需要提到：生成随机样本的方法也多种多样。默认情况下，每次采样都是我们熟悉的完全（伪）随机，不过利用半随机序列的某些属性，我们可以生成虽然是随机样本但具有一些有趣性质的样本向量。例如，我们可以对一种名为低差异序列的东西进行蒙特卡洛积分，该序列生成的仍然是随机样本，但样本分布更均匀：

        当使用低差异序列生成蒙特卡洛样本向量时，该过程称为拟蒙特卡洛积分。拟蒙特卡洛方法具有更快的收敛速度，这使得它对于性能繁重的应用很有用。

        鉴于我们新获得的有关蒙特卡洛（Monte Carlo）和拟蒙特卡洛（Quasi-Monte Carlo）积分的知识，我们可以使用一个有趣的属性来获得更快的收敛速度，这就是重要性采样。我们在前文已经提到过它，但是在镜面反射的情况下，反射的光向量被限制在镜面波瓣中，波瓣的大小取决于表面的粗糙度。既然镜面波瓣外的任何（拟）随机生成的样本与镜面积分无关，因此将样本集中在镜面波瓣内生成是有意义的，但代价是蒙特卡洛估算会产生偏差。

        本质上来说，这就是重要性采样的核心：只在某些区域生成采样向量，该区域围绕微表面半向量，受粗糙度限制。通过将拟蒙特卡洛采样与低差异序列相结合，并使用重要性采样偏置样本向量的方法，我们可以获得很高的收敛速度。因为我们求解的速度更快，所以要达到足够的近似度，我们所需要的样本更少。因此，这套组合方法甚至可以允许图形应用程序实时求解镜面积分，虽然比预计算结果还是要慢得多。

---

重要性采样

 方差估算：

随着N的增长，方差线性降低。但是估算正比于标准差，标准差以 速度降低，这也是蒙特卡罗方法的一个问题，估算收敛到正确结果的速度比较慢。

通过方差计算公式可知，当为常数时，方差为0，所以概率密度函数曲线形状越接近被积函数 方差越小，但是 很多时候我们并不知道 是什么样子的曲线。然而我们可以通过选择一个形状类似于 形状的 来实现减少方差。

 当我们使用有限的采样集时，生成均匀的随机方向并不是最佳方法。对于Specular IBL，我们对环境中的有光泽的材质进行积分，那么在高光反射（或者镜面反射）方向周围进行采样最为合理，这是因为大部分反射光都是由这个方向发出的。

通过使用概率密度函数pdf 来定义采样的最佳方向，函数峰值代表重要的采样区域，通过这种重要度采样可以减少方差，达到对积分的最佳近似。在接近高光反射方向，这种采样数需要较高的地方， pdf 值会变得较低，相当于提高了采样的数值(间接来说就是提升了次数)，相反在采样数较低的地方， pdf 值会比较高，相当于间接减少采样次数 。

---

低差异序列

使用伪随机数产生随机采样会造成方向分布不均匀，因为伪随机数之间并不了解彼此的信息，可能会产生丛聚，这会导致蒙特卡罗积分方程式中，预估的准确性较差，收敛速度慢。通过使用低差异序列替换伪随机数，我们可以提高准确度，它本质上可以更好地保证分配的方向。使用Low-Discrepancy Sequence来生成蒙特卡罗采样向量，这个过程被称为Quasi-Monte Carlo积分。Quasi-Monte Carlo方法有更快的收敛速度，使他能够胜任大型复杂的应用。

当使用低差异序列生成蒙特卡洛样本向量时，该过程称为拟蒙特卡洛积分。拟蒙特卡洛方法具有更快的收敛速度，这使得它对于性能繁重的应用很有用。

我们将使用重要性采样来预计算间接反射方程的镜面反射部分，该采样基于拟蒙特卡洛方法给出了随机地低差异序列。我们将使用的序列称之为Hammersley序列。Hammersley序列是基于Van Der Corpus 序列，该序列是把十进制数字的二进制表示镜像翻转到小数点右边得到。

float RadicalInverse_VdC(uint bits) 
{
    bits = (bits << 16u) | (bits >> 16u);
    bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
    bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
    bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
    bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
    return float(bits) * 2.3283064365386963e-10; // / 0x100000000
}
// ----------------------------------------------------------------------------
vec2 Hammersley(uint i, uint N)
{
    return vec2(float(i)/float(N), RadicalInverse_VdC(i));
}  

GLSL 的 Hammersley 函数可以获取大小为 N 的样本集中的低差异样本 i。

无需位运算的 Hammersley 序列

并非所有 OpenGL 相关驱动程序都支持位运算符（例如WebGL和OpenGL ES 2.0），在这种情况下，你可能需要不依赖位运算符的替代版本 Van Der Corpus序列：

float VanDerCorpus(uint n, uint base)
{
    float invBase = 1.0 / float(base);
    float denom   = 1.0;
    float result  = 0.0;

    for(uint i = 0u; i < 32u; ++i)
    {
        if(n > 0u)
        {
            denom   = mod(float(n), 2.0);
            result += denom * invBase;
            invBase = invBase / 2.0;
            n       = uint(float(n) / 2.0);
        }
    }

    return result;
}
// ----------------------------------------------------------------------------
vec2 HammersleyNoBitOps(uint i, uint N)
{
    return vec2(float(i)/float(N), VanDerCorpus(i, 2u));
}

请注意，由于旧硬件中的 GLSL 循环限制，该序列循环遍历了所有可能的 32 位，性能略差。但是如果你没有位运算符可用的话可以考虑它，它可以在所有硬件上运行。