【支持向量机SVM系列教程2】非线性SVM

2 非线性SVM

2.1 SVM问题的对偶化

在介绍非线性SVM之前，有必要先来看一下什么是SVM问题的对偶化，目的是：

1. 如何通过对偶化将线性SVM与非线性SVM联系起来；
2. 对偶问题是如何简化问题的求解的。

2.1.1 对偶的概念

大多数问题可以从两个角度来看待：

• Primal Problem（原问题）
• Dual Problem（对偶问题）

而对偶问题中有一个非常重要的性质——强对偶性，它是指：对偶问题的解即为原问题的解，两者的解相互等价。所以，当原问题的求解过于复杂时，我们可以绕个圈子：先求对偶问题的解，再来推出原问题的解，这样会使得问题的求解更加方便。

2.1.2 原问题

2.1.2.1 软间隔约束条件的改写

在上一章的线性SVM中，已经推导出了线性SVM 软间隔形式的目标函数，如下：
$$\begin{gathered} \underset{w,b,{\xi }_i}{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C\sum _{i=1}^m{\xi }_i \\ s.t.y_i({\mathbf{w}}^T{\mathbf{x}}_{\mathbf{i}}+b)⩾1-{\xi }_i \end{gathered}$$
该函数的优化的目标为：以 $w$ , $b$ 和 $\xi$ 为变量，最小化目标函数，同时保持约束条件被满足。

其中，上面的约束条件可改写为：
$$y_i({\mathbf{w}}^T{\mathbf{x}}_{\mathbf{i}}+b)-1+{\xi }_i⩾0$$

2.1.2.2 将约束条件添加进拉格朗日函数

通过构造拉格朗日函数，把约束条件加进拉格朗日函数中，可以简化问题的求解。该函数的形式为：

$$L(w,b,\xi ,\alpha ,\beta )$$
该函数需要在原带松弛变量的目标函数中添加如下两个约束：

1. 样本须“正确分类”的约束（主要约束）：

$$-\sum _{i=1}^m{\alpha }_{(}{y}_i({\mathbf{w}}^T{x}_i+b)-1+{\xi }_i)$$

其中，$\alpha$ 为 拉格朗日乘子 ，且 $\alpha ⩾0$ ，其用处为：

• 当样本被正确分类时，满足约束条件，括号内的约束函数值为大于等于0的有限值，此时，目标函数等价于：

  $$\underset{w,b,{\xi }_i}{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C\sum _{i=1}^m{\xi }_i$$
  这样的作为：“ 告知系统当前样本分类正确，需对 $w$ 和 $b$ 进行调整以最小化目标函数 “

• 当样本没有被正确分类时，括号内的约束函数值小于0，此时，α 取值为+∞，使得目标函数值→+∞，起到了“ 告知系统在样本分类错误时，无需再浪费时间进行优化 ” 的作用。

2. 松弛变量 $\xi$ 必须为非负数的约束：

$$-\sum _{i=1}^m{\beta }_i{\xi }_i$$

β 用来施加该约束。道理同 α。

通过 α 和 β 来控制这两个约束，一定程度上减少了算法的复杂度。

把上述两个约束添加到如下拉格朗日函数中：
$$L(w,b,\xi ,\alpha ,\beta )=\underset{w,b,{\xi }_i}{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C\sum _{i=1}^m{\xi }_i-\sum _{i=1}^m{\alpha }_i(y_i({\mathbf{w}}^T{x}_i+b)-1+{\xi }_i)-\sum _{i=1}^m{\beta }_i{\xi }_i$$

2.1.2.3 新的目标函数

上面已经求解出了拉格朗日函数，目标函数等价为：
$$\underset{\mathbf{w},\mathbf{b},\mathbf{\xi }}{\min }\underset{\mathbf{\alpha }⩾0,\mathbf{\beta }⩾0}{\max }L(w,b,\xi ,\alpha ,\beta )$$
但这样的话，调整 $w,b,\xi$ 进行最小化的操作仍然被放在外面，求解过程依然不好得到。

下面将该原问题转化为对偶问题，进一步简化求解过程。

2.1.3 对偶问题

2.1.3.1 由“强对偶”性质得到转化后的目标函数

利用强对偶性，可将上述目标函数转化为：
$$\underset{\mathbf{\alpha }⩾0,\mathbf{\beta }⩾0}{\max }\underset{\mathbf{w},\mathbf{b},\mathbf{\xi }}{\min }L(w,b,\xi ,\alpha ,\beta )$$

下面将进行详细推导，消除原问题中有关最小化的项，使式子被替换为由 $\alpha ,\beta$ 表达的形式。

2.1.3.2 KKT条件

KKT是一位科学家的名字，他指出了max-min问题中一定会成立的一些条件，称为KKT条件。利用这些条件可以对原变量中的 $w$, $b$, $\xi$ 进行转化。KKT条件主要分为如下两种：

• Stationarity条件

  当原变量和对偶变量的梯度为0时，优化效果达到最好，无法继续优化。

  由拉格朗日函数：

  $$L(w,b,\xi ,\alpha ,\beta )=\underset{w,b,{\xi }_i}{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C\sum _{i=1}^m{\xi }_i-\sum _{i=1}^m{\alpha }_i(y_i({\mathbf{w}}^T{x}_i+b)-1+{\xi }_i)-\sum _{i=1}^m{\beta }_i{\xi }_i$$

  • 对 $\mathbf{w}$ 的梯度为：
    KaTeX parse error: Got function '\boldsymbol' with no arguments as subscript at position 19: …igtriangledown_\̲b̲o̲l̲d̲s̲y̲m̲b̲o̲l̲ ̲w L=\boldsymbol…

  • 对 $b$ 的梯度为：
    KaTeX parse error: Got function '\boldsymbol' with no arguments as subscript at position 19: …igtriangledown_\̲b̲o̲l̲d̲s̲y̲m̲b̲o̲l̲ ̲b L=\boldsymbol…

• 对 $\xi$ 的梯度为：
  KaTeX parse error: Got function '\boldsymbol' with no arguments as subscript at position 19: …igtriangledown_\̲b̲o̲l̲d̲s̲y̲m̲b̲o̲l̲ ̲\xi L=C-\alpha-…
  这里可以得到：
  $$0⩽\alpha ⩽C$$

得到上面这些等式之后，就可以代入拉格朗日函数，消除原始问题中有关最小化的项，将问题转化成：

$$\underset{\alpha ⩾0}{\max }-\frac{1}{2}\sum _i\sum _j{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j+\sum _i{\alpha }_i$$
再去掉最前面的负号，转化为最小化问题：
$$\begin{gathered} \underset{\alpha ⩾0}{\min }\frac{1}{2}\sum _i\sum _j{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j-\sum _i{\alpha }_i \\ s.t.\sum _i{\alpha }_i{y}_i=0,0⩽{\alpha }_i⩽C \end{gathered}$$
这样就把每一个样本都带约束的复杂的基础型SVM问题转化成了对偶函数，只需要找到使得该式成立，且满足约束条件的 $\alpha$ 即可，很大程度上简化了问题的求解。

求出了该 α 之后，就可以求出 w ：
$$\mathbf{w}=\sum _i{\alpha }_i{y}_i{x}_i$$
进而得到如下模型函数（用来预测新样本）：
$$f(\mathbf{x})=w^T\mathbf{x}+b=\sum _i{\alpha }_i{y}_i{x}_i^T\mathbf{x}+b$$
将 $\mathbf{x}$ 替换为任一特定样本$x_j$，则上面的模型函数改写为：
$$f(x_i)=w^T{x}_i+b=\sum _{j=1}^m{\alpha }_j{y}_j{x}_j^T{x}_i+b$$
现在未知变量就只剩下了$b$。

• Complementary Slackness条件

  该条件的思想为：不等式取等号时，约束条件最严格。故：
  $$y_{i}f(x_i)-1=0$$
  即：
  $$y_i(\sum _j{\alpha }_j{y}_j{x}_j^T{x}_i+b)-1=0$$

  求得：
  $$b=y_i-\sum _j{\alpha }_j{y}_j{x}_j^T{x}_i$$

通过这两个KKT条件，就可以通过一个单一变量$\alpha$把 $w$ 和 $b$ 这两个非常重要的参数给推导出来。

2.1.4 向量内积

通过上面的推导我们已经得出了对偶化问题的目标函数如下：
$$\begin{gathered} \underset{\alpha ⩾0}{\min }\frac{1}{2}\sum _i\sum _j{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j-\sum _i{\alpha }_i \\ s.t.\sum _i{\alpha }_i{y}_i=0,0⩽{\alpha }_i⩽C \end{gathered}$$
求参数 $\mathbf{w}$ 的公式如下：
$$\mathbf{w}=\sum _i{\alpha }_i{y}_i{x}_i$$
求参数 $b$ 的公式如下：
$$b=y_j-\sum _i{\alpha }_i{y}_i{x}_i^T{x}_j$$
可以发现，上面的三条公式里都有一个相同的式子：$x_i^T{x}_j$，它表示当前样本向量$x_i$与其他任一样本向量$x_j$的内积。把 $x_i^T{x}_j$替换为核函数 $\kappa (x_i,x_j)$，即可得到 核SVM 。

这样我们就通过对偶问题把线性SVM和非线性SVM给联系起来了。

2.2 核函数

2.2.1 一般化形式

核函数 $\kappa (x_i,x_j)$ 实际上是内积的一般化形式：
$$\kappa (x_i,x_j)=\varphi (x_i{)}^T\varphi (x_j)$$
Φ 函数用于把 $x$ 从原始的特征空间 $X$ 映射到另一个特征空间 $Z$，它主要可分为如下几种：

• 线性特征映射（实际上就是线性SVM，前面已介绍）
  $$\varphi (x)=[x^1,x^2,x^3,...,x^d{]}^{T}Z={\mathbb{R}}^d$$

• 多项式特征映射

• 高斯特征映射

下面将介绍后两项。

2.2.2 多项式核

2.2.2.1 直观展示

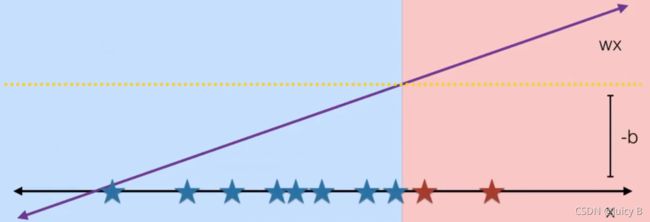
假设有一系列一维样本，使用线性分类器的分类效果如下:

可以看到该数据集可以被线性分开。

但对于如下的样本，显然无法用一条直线来分开。

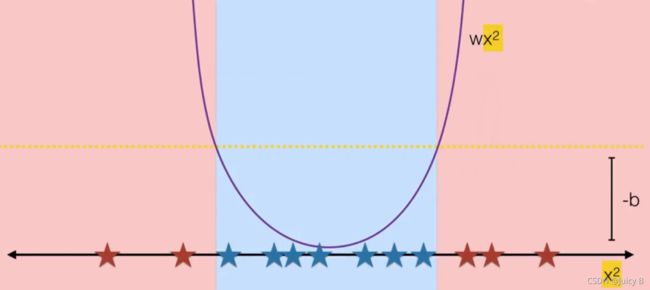
所以，考虑将数据集映射到$x^2$上，分类效果如下：

可以看到，将 x 映射到 $x^2$上，实现了很好的分类效果。这里就用到了多项式核。

2.2.2.2 公式表达

假设数据集中的每一个样本 $x$ 均由 $d$ 个特征组成：
$$x=[x^1,x^2,x^3,...,x^d]$$
对样本进行多项式映射有很多种方式，阶数不同，映射的效果不同。

• 2阶：将样本中任意可能的两个特征进行组合：

$$\varphi (x)=[x^1,...,x^d,x^1{x}^1,...,x^1{x}^d,...,x^d{x}^1,...,x^d{x}^d{]}^T,Z=R^{d^2}$$

• 3阶：将样本中任意可能的三个特征进行组合：

  $$\{x^1{x}^1{x}^1,x^1{x}^1{x}^2,...,x^1{x}^d{x}^d,...,x^d{x}^d{x}^d\}$$

• 更高阶的以此类推

对两个多项式映射进行下面的计算：
$$\kappa (x_i,x_j)=\varphi (x_i{)}^T\varphi (x_j)$$
就得到了多项式核。

2.2.3 高斯核

2.2.3.1 直观展示

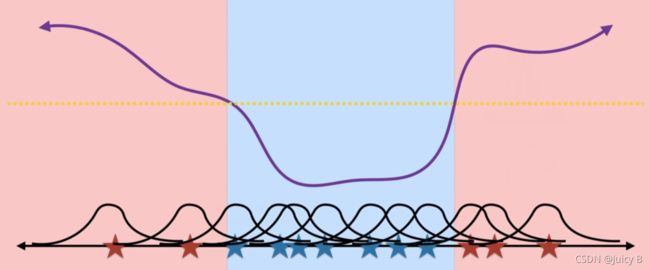
使用高斯核进行非线性分类的直观展示如下：

2.2.3.2 公式表达

高斯核函数的定义为：
$$\kappa (x_i,x_j)=exp(-\frac{1}{2{\sigma }^2}||x_i-x_j|{|}^2)$$
这种形式难以观察出高斯核函数的本质，所以下面要进行转化。

将上式展开，写成向量内积的形式，得：
$$\kappa (x_i,x_j)=exp(-x_i^T{x}_i)exp(-x_j^T{x}_j)exp(2x_i^T{x}_j)$$
再把高斯核函数写成如下形式：
$$\kappa (x_i,x_j)={\varphi }_{rbf}^T{\varphi }_{rbf}$$
其中：
$${\varphi }_{rbf}=\sqrt{exp(-x_i^T{x}_i-x_j^T{x}_j)}[{\varphi }^1(x{)}^T,{\varphi }^2(x{)}^T,...,{\varphi }^{\infty }(x{)}^T{]}^T$$
可以看到，高斯核的本质可以理解为：一个“无限维”的多项式展开。所以，使用高斯核，本质上是将特征变换到一个所谓的“无限维度”里面。这个“无限维度”是十分灵活的，在使用高斯核SVM求解非线性问题的时候，其具体的维度可以根据具体的问题自行拟定，具有很大的灵活性。这也使得高斯核被广泛地应用在SVM非线性问题的求解中。

2.2.3.3 主要的调参参数

令：
$$\gamma =\frac{1}{2{\sigma }^2}$$
则高斯核函数改写为：
$$\kappa (x_i,x_j)=exp(-\gamma ||x_i-x_j|{|}^2)$$
$\gamma$ 是高斯核方法中的一个主要参数，其取值对分类效果的影响有如下特点：

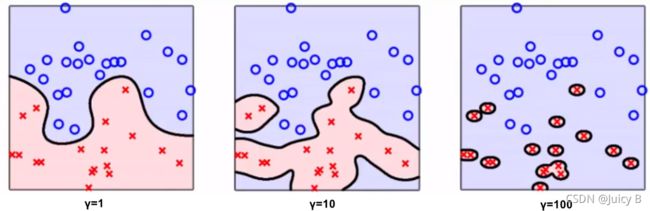
• $\gamma$ 很大时，$\sigma$ 很小，高斯分布显得 “瘦高” ，高斯核的作用范围较小，只限于样本附近，使得不同样本之间的联系很小，对于未知样本分类效果很差，而训练的准确率却很高，容易造成过拟合
• $\gamma$ 较小时，$\sigma$ 较大，高斯分布显得 “矮胖” ，高斯核的作用范围较大，使得不同样本之间的联系较紧密，对于未知样本分类效果较好，不容易造成过拟合

不同 $\gamma$ 取值的对分类效果的影响如下图所示：

可以看到 $\gamma$ 对分类效果的影响很大，实际使用时， $\gamma$ 也是我们的主要调参对象。

实际上，在RBF中，可以同时对 $\gamma$ 和 $C$ 进行调参。关于参数 $C$ 对于线性SVM的作用，前面已经介绍到。其实它对非线性SVM也有较大影响。先来看一下我们前面得到的对偶问题的目标函数：
$$\begin{gathered} \underset{\alpha ⩾0}{\min }\frac{1}{2}\sum _i\sum _j{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa (x_i,x_j)-\sum _i{\alpha }_i \\ s.t.\sum _i{\alpha }_i{y}_i=0,0⩽{\alpha }_i⩽C \end{gathered}$$
可以看到约束条件为$0⩽{\alpha }_i⩽C$，参数 $C$ 约束了变量 $\alpha$ ，进而对整个非线性SVM的求解结果产生了间接影响。所以实际使用中，对 $C$ 进行调参也是非常有必要的。

2.2.4 核技巧

上面多项式核和高斯核的求解过程会出现这样的问题：比如数据集中的每个样本都有1000个特征，如果想使用3阶多项式核，将会映射出1000×1000×1000=10亿个特征，这个计算量显然非常巨大，计算机难以承受。对于“无限维”的高斯核更是如此。想要解决这个问题，就需要用到核技巧，一种在高维空间中快速计算内积的方法。

由上面已经得到核函数的一般形式为：
$$\kappa (x_i,x_j)=\varphi (x_i{)}^T\varphi (x_j)$$
当使用多项式核时，我们希望能够绕过高维空间的表达，直接计算核函数。

所以，可以将核函数的内积替换成如下形式，不需要完整地展开特征向量中的每一项：
$$\kappa =(x_i^T{x}_j+1{)}^M$$
以 $M=2$ 为例（左边为所有二次项的内积）：
$$\kappa =(x_i^T{x}_j+1{)}^2=(x_i^T{x}_j)(x_i^T{x}_j)+2x_i^T{x}_j+1$$
采用这种形式会代替原始内积的形式，可以加快运算的速度。

当 $M$ 越大，即多项式的次数越大时，使用该技巧的速度提升越明显。

将这种形式推广到核矩阵中，可得如下公式：
$$K=(X^{T}X+1{)}^M$$
因为计算机处理矩阵内积的速度很快，所以采用这用这种技巧可以大幅增加运算速度。

2.2.5 sklearn中的非线性SVM

sklearn中实现非线性SVM的类有NuSVC和SVC两种。这两种类的使用方法非常类似，只是在底层的数学实现细节上有所不同。用得较多的还是SVC，这里以SVC为例。

2.2.5.1 原型

sklearn.svm.SVC(*, C=1.0, kernel='rbf', degree=3, gamma='scale', coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr', break_ties=False, random_state=None)

2.2.5.2 常用参数

• C：浮点数类型，默认值为1.0，表示惩罚系数（必须为正数）
• kernel：字符串类型，默认为’rbf’，表示要使用的核函数
  • linear：线性核
  • poly ：多项式核
  • rbf：高斯核
  • sigmoid：sigmoid核
• degree：整型，默认值为3
  • kernel='poly'时，表示多项式核的次数
  • kernel其他时，自动忽略该参数
• gamma：字符串类型，默认为’scale’
  • scale：gamma的值为 $1/(n\_features\times X.var())$
  • auto： gamma的值为 $1/n\_features$
• tol：浮点数类型，默认为1e-4，表示对损失的容忍度，损失降低到 tol 时，停止训练
• max_iter：整型，默认为1000，表示训练的最大迭代次数

2.2.5.3 常用属性

• coef_： 数组，给出各个特征的权重(w)
• support_vectors_： 数组，给出所有的支持向量

2.2.5.4 常用方法

• fit(X, y)：训练模型

• predict(X)：用模型进行预测，返回预测值

• score(X, y[, sample_weight])：返回预测的准确率

• decision_function：求解各个样本点到超平面（高维决策边界）的距离（在线性SVM中是各个样本点到二维决策边界的距离）

2.3 实例2：sklearn中非线性SVM的调参及可视化

前面探索了如何绘制线性SVM分类器的决策边界和大间隔，以及不同参数 $C$ 的值对线性分类效果的影响。下面将对高斯核SVM的调参过程进行探索和可视化，并总结出调参时需要注意的地方。

2.3.1 数据集的加载与显示

这里使用带噪声的月亮数据集做演示。代码如下：

# 生成月亮数据集，加上20%的随机噪声
X, y = make_moons(n_samples=200, noise=0.2, random_state=42)

def plot_dataset(X, y, axes):
    plt.plot(X[:, 0][y==0], X[:, 1][y==-1], "bs")
    plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
    plt.axis(axes)
    plt.grid(True, which='both')
    plt.xlabel(r"$x_1$", fontsize=20)
    plt.ylabel(r"$x_2$", fontsize=20, rotation=0)

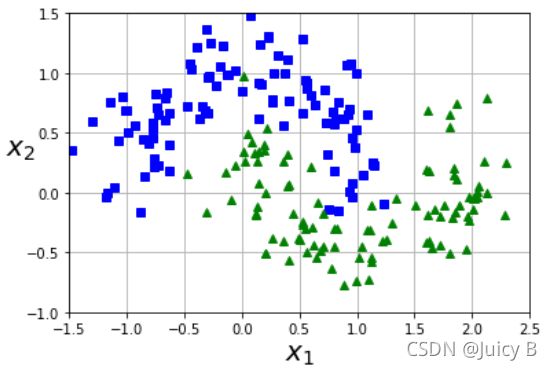
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()

输出结果如下图：

该数据集呈现出一种“双龙戏珠”的姿态，非常适合用来演示非线性SVM的分类效果。

2.3.2 对数据集进行标准化

前面已经通过例子展示过对数据集进行标准化的重要性。标准化的代码如下：

scaler = StandardScaler()
X = scaler.fit_transform(X)

2.3.3 网格搜索

这部分的思路为：

1. 定义较大的参数范围，用于绘制热力图，实现对不同参数组合验证准确率高低的直观可视化，使得网格搜索的中间过程不再神秘，也有利于我们理解不同参数组合下非线性SVM中的行为；
2. 将该热力图划分成不同区域进行分析，总结出调参需要注意的地方。

2.3.1 定义网格搜索，获取最佳结果

# C的范围：10^-5 ~ 10^6
Cs = np.logspace(-5, 6, 12)
# γ 的范围：10^-5 ~ 10^5
gammas = np.logspace(-5, 6, 12)
# 定义网格搜索范围
param_grid = dict(gamma = gammas, C = Cs)
# 定义k折验证的方法
cv = StratifiedShuffleSplit(n_splits=5, test_size = 0.3, random_state=1)
# SVC模型用高斯SVM（默认方法）
model = SVC()
# 网格搜索
grid = GridSearchCV(model, param_grid=param_grid, cv=cv, n_jobs=-1)
grid.fit(X, y)
# 打印出最佳结果
print("The best parameters are %s with a score of %0.2f."
      % (grid.best_params_, grid.best_score_))

输出结果如下：

The best parameters are {‘C’: 1.0, ‘gamma’: 1.0} with a score of 0.97.

这样做只能打印出最佳的一个结果，网格搜索的中间结果却不得而知。为了使得整个网格搜索的中间结果更加直观，接下来将会将网格搜索的所有中间结果用热力图的形式表示出来。

2.3.2 使用热力图表示网格搜索的中间验证准确率

# 获取网格搜索过程中各种不同参数组合的验证准确率
scores = grid.cv_results_['mean_test_score']
scores = scores.reshape(len(Cs), len(gammas))

plt.figure(figsize=(8, 6))
plt.subplots_adjust(left=0.2, right=0.9, bottom=0.2, top=0.9)
plt.imshow(scores, interpolation='nearest', cmap=plt.cm.hot)
plt.xlabel('gamma')
plt.ylabel('C', rotation=0)
plt.colorbar()
plt.xticks(np.arange(len(gammas)), gammas, rotation=45)
plt.yticks(np.arange(len(Cs)), Cs)
plt.title('Validation accuracy')
plt.show()

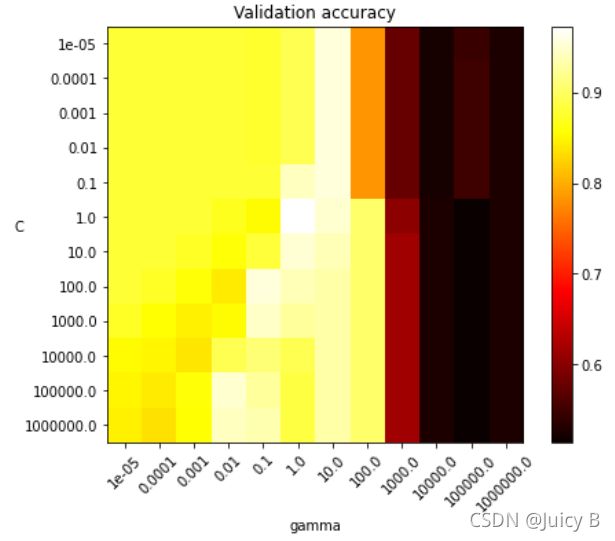
输出结果如下：

图中，颜色越亮，越白，表示对应参数组合的验证准确率越高。因此，通过观察上图，我们就可以非常直观地看出验证准确率最高的区域，从而很快找到对应的最佳参数组合。

显然，当 $C=1.0,\gamma =1.0$ 时，对应的色块颜色最亮，最接近白色，由此可判断其对应的验证准确率最高。这也刚好与上面打印出来的结果一致。

2.3.3 调参规律分析

接下来对将上图进行更加细致的分析，分析的方向主要分为下面两个：

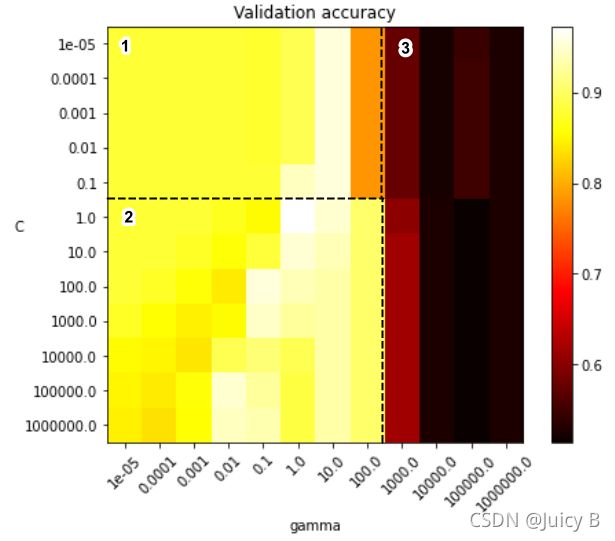
1. 按照色块的颜色深浅，可以大致将上图划分成三个区域：

   

   • 区域1：颜色以黄色居多，验证准确率大多在0.85到0.95之间，总体准确率比区域2稍低；
   • 区域2：颜色较亮的色块比区域1多，且包含最佳结果，是参数取值范围相对合理的区域；
   • 区域3：总体颜色很深，验证准确率均较低，参数取值范围不合理。

2. 按照参数值变化的角度，可以分为如下两个方向：

   • 横向：从左往右 $\gamma$ 的值逐渐增大
   • 纵向：从上到下 $C$ 的值逐渐减小

3. 综合上述两个角度，可以观察出如下规律：

   • 当 $\gamma ⩾1000.0$ 时，通过纵向对比，发现调整参数 $C$ 对准确率的提升作用很小，或者说几乎没有作用，并且总体的准确率也过低。所以 $\gamma$ 的值不应设置得过大；
   • 当 $\gamma ⩽0.001$时，通过纵向对比，发现参数 $C$ 要超过$1000.0$才能对模型有提升作用，在实际使用中会造成搜索的计算量过大，所以$\gamma$ 的值也不应设置得过小；
   • 当 $0.01⩽\gamma ⩽100$（取值适中）时，通过纵向对比，发现调整参数 $C$ 对模型的提升作用较明显，且 $C$ 的范围不会过大，大概集中在$0.1$ 到 $10$ 之间。所以，在实际调参中，比较可行的步骤为：
     • 先固定参数 $C$，拟定一个大小适中的 $\gamma$ 搜索范围（一般为 $0.01⩽\gamma ⩽100$）
     • 从上一步中挑选出准确率较高的 $\gamma$ 值，对 $\gamma$的搜索范围做进一步缩小
     • 再在上一步 $\gamma$ 范围的基础上，拟定一个大小适中的 $C$ 的搜索范围（一般为$0.1⩽C⩽10$， 综合两者进行网格搜索。

2.3.4 将网格搜索的结果进行可视化

接下来，我们取热力图中左下角的一个8×8区域（对应了64组不同的参数组合）用来进行分类效果的可视化，这有利于我们从视觉上直观地将不同参数组合所对应模型的分类效果与验证准确率一一对应起来，这对观察调参过程中参数的行为具有重要的意义。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-52dU4J6m-1632991488577)(234.png)]

进行网格搜索中间结果可视化的步骤为：

1. 定义要绘制曲线的网格点；
2. 将所有网格点分别送入不同分类器的decision_function 函数中进行运算，得到每个点到超平面的距离（这个超平面就是高斯核SVM拟合出来的决策超平面）
3. 将上一步求得的结果进行可视化。

前两步分别由如下两点实现：

1. numpy中的类c_ ；
2. decision_function 函数。

这两个知识点对于理解这个过程至关重要，所以下面将进行展开。

2.3.4.1 numpy中的类 c_

该类常配合 np.meshgrid函数一起使用。下面举一个简单的例子来看一下该函数的用法。

# x = [1,2,3,4,5,6]
x = np.arange(1, 7)
# y = [1,2,3,4,5,6]
y = np.arange(1, 7)

xx, yy = np.meshgrid(x, y)

xxr = xx.ravel()
print("xxr:\n ", xxr)

yyr = yy.ravel()
print("yyr:\n ", yyr)

输出结果：

xxr:
[1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6]
yyr:
[1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 5 5 5 5 5 5 6 6 6 6 6 6]

通过函数np.meshgrid，得到了xx，yy，分别为36个点所对应的横坐标和纵坐标。

接下来下面来看一下类 c_ 的用法。np.c_将36个点的横纵坐标一一对应起来，得到了36个点的二维坐标：

np.c_[xxr, yyr][:5]

输出结果：

[[1 1]
[2 1]
[3 1]
[4 1]
[5 1]]

…

通过上面的过程，我们就得到了网格中36个点的坐标。运用上述方法，就可以绘制更加复杂、数量更多的网格点。这为我们下面使用decision_function 函数奠定了基础。

2.3.4.2 decision_function 函数

以上面36个点的例子为例，对于高斯核SVM，decision_function函数内部的工作过程如下：

1. 用高斯核SVM分类器对这36个点组成的数据集进行拟合，得到决策超平面；

2. 使用上面的方法获取这36个点的二维坐标；

3. 将这36个点的二维坐标代入decision_function 函数中进行计算，求出各个点到决策超平面的有符号距离。

2.3.4.3 分类结果的可视化

在了解了上面的原理之后，将这36个点扩展成更多、更复杂的网格点，就可以对月亮数据集中的分类结果进行可视化。代码如下：

# 定义上图中gamma和C的参数范围
gammas_1 = gammas[0:8]
Cs_1 = Cs[4:12]

# 定义分类器列表
clfs = []
for C in Cs_1:
	for gamma in gammas_1:
        clf = SVC(C = C, gamma = gamma)
        clf.fit(X, y)
        clfs.append((C, gamma, clf))    
        
# 定义用于绘制决策边界的网格点的横坐标和纵坐标
xx, yy = np.meshgrid(np.linspace(-3, 3, 200), np.linspace(-3, 3, 200))

for (k, (C, gamma, clf)) in enumerate(clfs):
    # Z记录了各个点到决策超平面的距离
    Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
    if k == 0:
        # 此时Z的形状为(40000,1)
        print("Before reshaped: ", Z.shape)
    # 将Z转化为网格点的形式
    Z = Z.reshape(xx.shape)
    if k == 0: 
        # 此时Z的形状为(200, 200)
        print("After reshape: ", Z.shape)

    # 将Z的结果进行可视化
    plt.subplot(len(Cs_1), len(gammas_1), k + 1)
    if np.equal(gamma, 1.0) and np.equal(C, 1.0):
        # 网格搜索的最佳结果所对应的标题打成红色
        plt.title("gamma=$10^{%d}$, C=$10^{%d}$"%(np.log10(gamma),np.log10(C)), size='medium', color='red') 
        # 打印出最佳结果所对应的Z值（即各个点到决策超平面的距离）
        print("Best parameters with Z=\n", Z)
        
    plt.title("gamma=$10^{%d}$, C=$10^{%d}$" % (np.log10(gamma), np.log10(C)), size='medium')

    # Z值越大，对应的颜色越深
    plt.pcolormesh(xx, yy, -Z, cmap=plt.cm.coolwarm)
    # 画出数据集中的样本点
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.RdYlBu, edgecolors='face')
    # 每个图均不设置横纵轴名称
    plt.xticks(())
    plt.yticks(())
    plt.axis('tight')   

输出结果如下：

Before reshaped: (40000,)
After reshape: (200, 200)

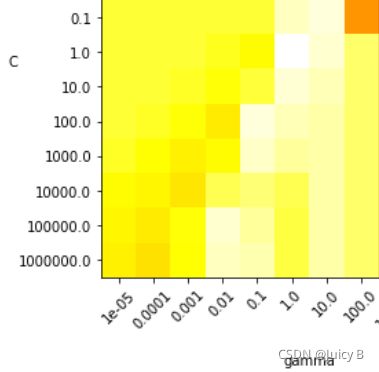
上图的结果与下面的热力图一一对应：

中间呈现”双龙戏珠“姿态的点集是模型要拟合的数据集，其中，蓝点表示数据集中的正样本点，红点表示数据集中的负样本点。数据集之外的其他部分是各分类器对网格点调用decision_function 函数之后求得的结果，其中：

• 蓝色部分为正值，表示当前网格点到决策平面的距离为正，网格点被预测为正类。蓝色越深，表示该网格点到决策平面的距离越远，越浅则距离越近；
• 红色部分为负值，表示当前网格点到决策平面的距离为负，网格点被预测为负类。红色越深，表示该网格点到决策平面的距离越远，越浅则距离越近。

线性SVM的基本思想是“最大化分类间隔”，实际上非线性SVM的思想也是如此，只不过分类边界被扩展到了高维空间，称为**“决策超平面”，这个“分类间隔”也被扩展成“高维空间上的分类间隔”**。因此，当数据集样本点附近的颜色很深时，就表示拟合出来的模型使得“高维空间上的分类间隔”较大，该非线性SVM模型就是较好的分类模型。由此就可以总结出如下规律：

1. $\gamma =1.0$ 时，数据集样本点周围的颜色很深，表示当前模型的分类间隔很大，并且对各个网格点的计算结果与数据集分布的走势比较契合，此时模型对数据集的拟合效果很好。这时，调整参数 $C$ 有助于找到最佳结果；
2. $\gamma ⩾10.0$时，数据集样本点周围的颜色很浅，表示当前模型的分类间隔很小，模型出现了过拟合的情况，分类效果很差，此时就算调整参数 $C$ 也无法缓解过拟合的情况；
3. $\gamma ⩽0.01$时，虽然数据集样本点周围的颜色也比较深，但是网格点的计算结果与数据集的走势不够契合，模型出现了欠拟合，，此时调整参数 $C$ 也对模型的改善作用也不大。

在实际使用中，可以利用上述方法进行可视化分析，这样可以对最佳参数的寻找起到引导作用，避免走弯路。