Game101现代计算机图形学入门学习笔记(七)
光线追踪
- 一、光线追踪
-
- 1、为什么要使用光线追踪?
- 二、基础光线追踪算法
- 1、光线
- 2、光线投射
-
- 1、着色过程
- 3、递归光线追踪 (Whitted-Style)
-
- 1、基本过程
- 2、光线-表面相交
-
- 1、光线方程
- 3、轴对称包围盒(AABB)
-
- 1、Uniform grids
- 2、空间划分
- 3、BVH(物体划分)
- 4、比较
- 四、辐射度量学
-
- 1、为什么需要辐射度量学
- 2、概念介绍
-
- 1、Radiant Energy
- 2、Radiant flux
- 3、Radiant Intensity
- 4、Irradiance
- 5、Radiance
- 6、Irradiance和Radiance
- 3、双向反射分布函数(BRDF)
-
- 1、反射方程
- 2、渲染方程
- 3、全局光照
- 五、蒙特卡洛积分
-
- 1、为什么
- 2、定义
- 3、做法
- 六、路径追踪
-
- 1、为什么
- 2、做法
-
- 1、蒙特卡洛积分近似
- 2、问题:假设有N根光线,反射M次,对于一个像素的射线是 N M N^M NM,指数级增加且计算量大。
- 3、问题:算法什么时候停止?
- 4、问题:光线在从物体打到光源是存在一定概率的,它与光源自身大小相关,如果光源过小,会使得大量光线无法打到光源
- 5、问题:光线会被物体挡住
- 七、参考和引用
一、光线追踪
1、为什么要使用光线追踪?
- 光栅化无法处理好全局信息进行渲染的效果,如软阴影、Glossy反射、间接光照
- 光栅化速度很快,但质量相对较低。而光线追踪质量精确,速度慢。
- 光栅化是实时的,光线追踪是离线的。
二、基础光线追踪算法
1、光线
该课程对光线概念的假设:
- 光线沿直线传播
- 光线之间不会碰撞
- 光线从光源出发最后到达人眼。(光线的可逆性,沿着传播路径往回寻找,也一定能找到光源。)
2、光线投射
1、从相机位置,向每个像素投射一条光线用于成像。
2、从像素中对应物体的每个位置投射回光线,检查是否在阴影中。
1、着色过程
从视点发射一条光线,通过成像平面(某个像素)投射至物体,然后从物体发出光线至光源检查其是否在阴影中,如果不在阴影中,就可以通过着色方案对这个像素进行着色。

3、递归光线追踪 (Whitted-Style)
1、基本过程
1、从视点从成像平面发出光线,检测是否与物体碰撞
2、如果有碰撞,根据权值生成折射和反射部分
3、递归计算生成的光线
4、所有光线交点在检测到达光源后,都与光源计算一次着色
5、将所有着色通过某种加权叠加起来,得到最终成像平面上的像素的颜色

2、光线-表面相交
1、光线方程
光线:有一个起点和其方向向量。
r ( t ) = o + t d ⃗ , 0 ≤ t < ∞ r(t)=o+t\vec{d},0\leq t<\infty r(t)=o+td,0≤t<∞,t为时间
- 与球体相交
球体:表面点p到圆心的方程:
( p − c ) 2 − R 2 = 0 (p-c)^2-R^2=0 (p−c)2−R2=0
交点即在光线上又在球体表面上。
( o + t d ⃗ − c ) 2 − R 2 = 0 (o+t\vec{d}-c)^2-R^2=0 (o+td−c)2−R2=0
a = d ⋅ d a=d \cdot d a=d⋅d
b = 2 ( o − c ) ⋅ d b=2(o-c)\cdot d b=2(o−c)⋅d
c = ( o − c ) 2 − R 2 c=(o-c)^2-R^2 c=(o−c)2−R2
t = − b ± b 2 − 4 b a 2 a t=\frac{-b\pm\sqrt{b^2-4ba}}{2a} t=2a−b±b2−4ba - 与隐式平面相交
隐式平面: f ( p ) = 0 f( p)=0 f(p)=0
f ( o + t d ⃗ ) = 0 f(o+t\vec{d})=0 f(o+td)=0 - 与三角形相交
3、轴对称包围盒(AABB)
先判断光线与包围物体的盒子来粗略判定光线是否与物体相交,再精确判断是否与物体相交。
t e n t e r = m a x ( t m i n ) t_{enter}=max(t_{min}) tenter=max(tmin)
t e x i t = m i n ( t m a x ) t_{exit}=min(t_{max}) texit=min(tmax)
- t e x i t t_{exit} texit<0,包围盒在光线后面,没有相交
- t e x i t t_{exit} texit>0, t e n t e r t_{enter} tenter<0,光线在包围盒里面,有交点
- 光线与包围盒相交当且仅当 t e n t e r t_{enter} tenter< t e x i t t_{exit} texit&& t e x i t t_{exit} texit>0
1、Uniform grids
将包围盒划分成很多个大小相同的格子,然后判断光线与格子的相交情况,再判断与格子内物体的相交情况。
步骤:
1、找到包围盒。
2、划分成一个个格子。
3、光线与物体相交的格子填好。
适合物体较为密集的场景。
缺点:
1、受分辨率影响,分辨率太小就失去了划分的意义,分辨率太大也不好。
2、不适合物体较为稀疏的场景,浪费大量时间在光线与格子的求交上。
2、空间划分
通常有 八叉树 、KD树 以及 BSP树 三种划分方案。
- 八叉树: 每次迭代都将区域重新切分为均匀四块,按一定规则停止切分。
- BSP树:每次都是沿着一定方向进行切分(非水平或竖直)
- KD树预处理
每次划分都会生成新的两块区域,然后再在两块区域内进行划分,直至满足递归截止条件。
数据结构:

中间节点存储了:
1、划分后的轴
2、划分后的切分平面
3、子节点的指针
叶子节点存储了区域中包含的物体
遍历过程:
1、发射光线从根节点出发,分别判断光线与左右节点是否相交,若相交则进入下一步;否则,则与节点不相交
2、递归判断相交直至叶子节点,若与叶子节点相交,进入下一步
3、依次判断叶子节点存储物体与光线的相交情况
缺点:
1、建立过程中需要考虑三角形与包围盒的求交问题
2、物体可能与多个包围盒相交
3、BVH(物体划分)
在场景中对物体进行划分。
本质是将一个场景用一个包围盒包住,然后按照一定划分方案将盒子划分成不同的子区域,不同子区域都需要包含三角形,最终划分到叶子节点时,每个叶子节点就包含了一些三角形,即包含了对应的一些物体。
过程
1、找到包围盒。
2、递归地将包围盒划分成包含一些物体的子集(课程上的划分规则是沿着三角形分布的最长的轴)
3、重新计算子集的包围盒。
4、达到递归结束条件就停止。
如何划分节点
1、按轴的次序划分
2、按最长轴划分
3、在物体三角形数目的最中间对物体进行划分(最中间指的是划分后,两边的三角形数目基本一致)
数据结构
中间节点:该节点对应的包围盒和子节点的指针
叶子节点:该节点对应的包围盒和包围盒里面的物体
遍历过程就是递归的,类似于遍历二叉树。
4、比较
- 空间划分
1、没有重叠区域。
2、一个物体可能在多个区域中。 - 物体划分
1、划分物体到独立的子集中。
2、每个子集的包围盒可能存在重叠的情况。
四、辐射度量学
1、为什么需要辐射度量学
因为需要对物理世界的光做更加真实的描述,而辐射度量学是具有物理意义的,它相较于 blinn phong 等光照模型,能够更加精确、真实地描述光照 。
2、概念介绍
1、Radiant Energy
电磁辐射的能量,单位用焦耳表示
Q [ J = J o u l e ] Q[J=Joule] Q[J=Joule]
2、Radiant flux
单位时间的能量。
Φ = d Q d t [ W = W a t t ] [ l m = l u m e n ] \Phi=\frac{dQ}{dt}[W=Watt][lm=lumen] Φ=dtdQ[W=Watt][lm=lumen]
3、Radiant Intensity
每单位立体角的能量。
立体角:球面上的面积与半径平方之比。
Ω = A r 2 \Omega=\frac{A}{r^2} Ω=r2A
4、Irradiance
单位区域面积、单位时间内接收到的辐射能量
E ( x ) = d x d A E(x)=\frac{dx}{dA} E(x)=dAdx
- 兰贝特余弦定律
平面上的Irradiance与光线和平面法线的夹角余弦。

当光源离物体表面越远,角度是不变的,但辐射到的面积却是增大的,所以 irradiance 是逐渐衰减的。而Radiant Intensity只跟角度有关,不变。
5、Radiance
用来描述环境中的光线的分布
- 与光线有关的属性
- 渲染是在计算radiance
是指单位立体角、单位投影面积所辐射的能量
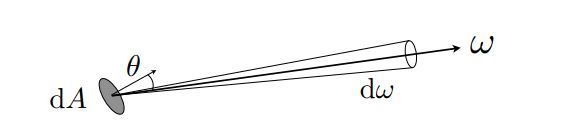
L ( p , w ) = d 2 Φ ( p , w ) d w d A c o s θ L(p,w)=\frac{d^{2}\Phi(p,w) }{dwdA cos\theta} L(p,w)=dwdAcosθd2Φ(p,w)
可以理解为:每单位立体角上的Irradiance,每单位面积上的Radiant Intensity - Incident Radiance
光源到达物体时每单位立体角的能量。(与入射有关)

L ( p , w ) = d E ( p ) d w c o s θ L(p,w)=\frac{dE(p)}{dw cos\theta} L(p,w)=dwcosθdE(p) - Exiting Radiance
每单位面积离开物体表面的能量。(与出射有关)

L ( p , w ) = I ( p , w ) d A c o s θ L(p,w)=\frac{I(p,w)}{dA cos\theta} L(p,w)=dAcosθI(p,w)
6、Irradiance和Radiance
d E ( p , w ) = L i ( p , w ) c o s θ d w dE(p,w)=L_i(p,w)cos\theta dw dE(p,w)=Li(p,w)cosθdw
E ( p ) = ∫ H 2 L i ( p , w ) c o s θ d w E(p)=\int_{H^2}L_i(p,w)cos\theta dw E(p)=∫H2Li(p,w)cosθdw
Irradiance就相当于单位面积上收到的所有方向上的能量。

3、双向反射分布函数(BRDF)
解决从某个方向辐射到表面的能量,它所反射到其他方向的能量分布问题。
1、反射方程
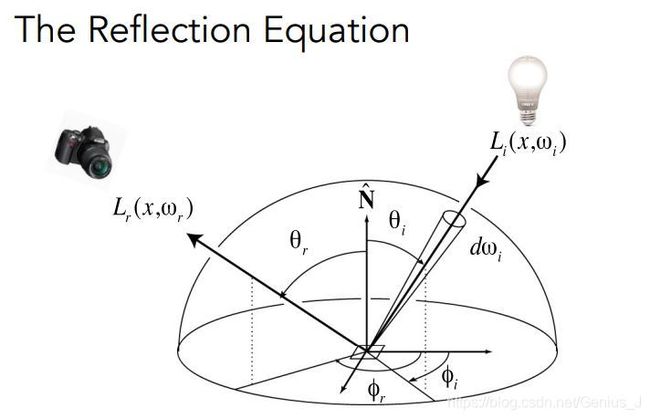
L r ( p , w r ) = ∫ H 2 f r ( p , w i → w r ) L i ( p , w i ) c o s ( θ i ) d w i L_r(p,w_r)=\int_{H^2}fr(p,w_i \rightarrow w_r)L_i(p,w_i)cos(\theta_i)dw_i Lr(p,wr)=∫H2fr(p,wi→wr)Li(p,wi)cos(θi)dwi
挑战:递归 方程
反射radiance来自入射的radiance,入射的radiance除了来自光源还有来自其他点反射的radiance。
2、渲染方程
L o ( p , w o ) = L e ( p , w o ) + ∫ Ω + f r ( p , w i , w o ) L i ( p , w i ) ( n , w i ) d w i L_o(p,w_o)=L_e(p,w_o)+\int_{\Omega+}fr(p,w_i ,w_o)L_i(p,w_i)(n,w_i)dw_i Lo(p,wo)=Le(p,wo)+∫Ω+fr(p,wi,wo)Li(p,wi)(n,wi)dwi
L e ( p , w o ) L_e(p,w_o) Le(p,wo):物体自身发光。
当光源为点光源:

L r ( x , w r ) = L e ( x , w r ) + ∑ f ( p , w i , w r ) L i ( x , w i ) ( n , w i ) ( w i , n ) L_r(x,w_r)=L_e(x,w_r)+\sum f(p,w_i ,w_r)L_i(x,w_i)(n,w_i)(w_i,n) Lr(x,wr)=Le(x,wr)+∑f(p,wi,wr)Li(x,wi)(n,wi)(wi,n)
当光源为面光源:
L r ( x , w r ) = L e ( x , w r ) + ∫ Ω f r ( x , w i , w r ) L i ( x , w i ) c o s ( θ i ) d w i L_r(x,w_r)=L_e(x,w_r)+\int_{\Omega}fr(x,w_i ,w_r)L_i(x,w_i)cos(\theta_i)dw_i Lr(x,wr)=Le(x,wr)+∫Ωfr(x,wi,wr)Li(x,wi)cos(θi)dwi
可以简化为如下形式 ,K 是反射操作符, E 为自发光项,L 为辐射出来的能量:
L = E + K L → L = ( I + K + K 2 + … ) E L=E+KL \rightarrow L=(I+K+K^2+\dots)E L=E+KL→L=(I+K+K2+…)E
3、全局光照
直接光照(KE)+间接光照( ( K 2 + … ) E (K^2+\dots)E (K2+…)E)。
五、蒙特卡洛积分
1、为什么
因为精确积分比较困难。
2、定义
- 一种近似求解积分的方法
- 它在所求定积分的函数中随机取样多次,分别对取样得到的 f(x) 值和定积分上下限的矩形求面积,然后将这些面积平均,以近似求解定积分。
3、做法
定义积分: ∫ b a f ( x ) d x \int^{a}_bf(x)dx ∫baf(x)dx
随机值: X i ∼ p ( x i ) X_i \sim p(x_i) Xi∼p(xi)
蒙特卡洛估计: F N = 1 N ∑ i = 1 N f ( X i ) p ( X i ) F_N=\frac{1}{N}\sum^N_{i=1}\frac{f(X_i)}{p(X_i)} FN=N1∑i=1Np(Xi)f(Xi)
采样越多,方差越小。
在x上采样,在x上积分。
六、路径追踪
1、为什么
whitted型光线追踪总是在镜面平面发生反射,在漫反射平面不发生反射,不适合glossy材质物体。
对于以上问题,渲染方程是对的。
2、做法
1、蒙特卡洛积分近似
不考虑自身发光,渲染方程:
L o ( p , w o ) = ∫ Ω + f r ( p , w i , w o ) L i ( p , w i ) ( n , w i ) d w i L_o(p,w_o) =\int_{\Omega+}fr(p,w_i ,w_o)L_i(p,w_i)(n,w_i)dw_i Lo(p,wo)=∫Ω+fr(p,wi,wo)Li(p,wi)(n,wi)dwi
f ( x ) 是 f r ( p , w i , w o ) L i ( p , w i ) ( n , w i ) f(x)是fr(p,w_i ,w_o)L_i(p,w_i)(n,w_i) f(x)是fr(p,wi,wo)Li(p,wi)(n,wi)
pdf就是采样方式 ,如何进行采样。
这里使用均匀采样 p d f ( x ) 就 是 1 2 π pdf(x)就是\frac{1}{2\pi} pdf(x)就是2π1
L o ( p , w o ) = ∫ Ω + f r ( p , w i , w o ) L i ( p , w i ) ( n , w i ) d w i ≈ 1 N ∑ i = 1 N f r ( p , w i , w o ) L i ( p , w i ) ( n , w i ) p d f ( w i ) L_o(p,w_o) =\int_{\Omega+}fr(p,w_i ,w_o)L_i(p,w_i)(n,w_i)dw_i\approx \frac{1}{N}\sum^N_{i=1}\frac{fr(p,w_i ,w_o)L_i(p,w_i)(n,w_i)}{pdf(w_i)} Lo(p,wo)=∫Ω+fr(p,wi,wo)Li(p,wi)(n,wi)dwi≈N1∑i=1Npdf(wi)fr(p,wi,wo)Li(p,wi)(n,wi)
过程:
1、随机采样N个入射方向。
2、判断每一条光线是否能反向打到光源,能则代入公式计算,累加。
3、返回结果

以上是只考虑了直接光照,还要考虑间接光照,继而形成全局光照。
要加上入射光线是否能反向打到某个物体,如果能,则要计算相应的结果。

2、问题:假设有N根光线,反射M次,对于一个像素的射线是 N M N^M NM,指数级增加且计算量大。
仅仅使用一根光线,即采样一次。

N=1就是路径追踪, N ≠ 1 N\not=1 N=1是分布式路径追踪。
对于一个像素选取不同的位置打入射线以求解着色:
1、在一个像素内,取N个不同位置。
2、每个位置与摄像机相连,如果达到某个物体,就要计算着色。

3、问题:算法什么时候停止?
现实中光线弹射是不会停止,不能限制弹射次数。
引入俄罗斯轮盘赌RR,类似p-坚持型CSMA,p概率发射光线,要么不发射光线。期望是 E = P ∗ ( L o / P ) + ( 1 − P ) ∗ 0 = L o E=P*(L_o/P)+(1-P)*0=L_o E=P∗(Lo/P)+(1−P)∗0=Lo

4、问题:光线在从物体打到光源是存在一定概率的,它与光源自身大小相关,如果光源过小,会使得大量光线无法打到光源
从光源进行采样。
蒙特卡洛积分要求在x上采样,在x上积分。
改写在物体上积分,改成在光源积分:

将radiance分成两部份:
5、问题:光线会被物体挡住
连接像素与光源,判断路径上是否有其他物体。
七、参考和引用
[1] bilibili:GAMES101-现代计算机图形学入门-闫令琪
[2] 光线追踪(基本原理).pdf
[3] 计算机图形学九:几何1—隐式曲面(代数形式,CSG, 距离函数,分型几何)与显式曲面
[4]CSDN:GAMES101-现代计算机图形学学习笔记(13)
[5]计算机图形学十:几何2—贝塞尔曲线(Bézier Curves)与贝塞尔曲面(Bézier Surfaces)
[6] 光线追踪(加速结构).pdf
[7] 光线追踪(辐射度量学、渲染方程与全局光照).pdf
[8]计算机图形学十一:几何3—曲面细分(Mesh subdivision)与曲面简化(Mesh Smplication)
[9] 光线追踪(蒙特卡洛积分与路径追踪) .pdf
[10] CSDN:GAMES101-现代计算机图形学学习笔记(14)
[11] CSDN:GAMES101-现代计算机图形学学习笔记(15)
[12] CSDN:GAMES101-现代计算机图形学学习笔记(16)

