【机器学习】(西瓜书习题8.3)编程实现AdaBoost模型,以不剪枝决策树为基学习器,在西瓜数据集3.0a上训练一个AdaBoost集成,并与教材图8.4进行比较
(1)问题理解与分析
编程实现AdaBoost模型,不剪枝决策树为基学习器,在西瓜数据集3.0a上训练一个AdaBoost集成,并与教材图8.4进行比较。
(2)AdaBoost算法原理阐述
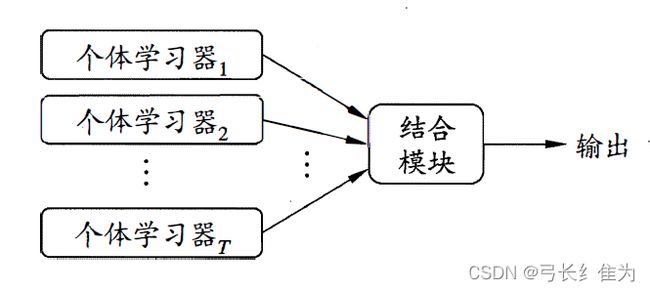
集成学习是一种通过构建并结合多个学习器来完成学习任务的机器学习方法。同质集成中的个体学习器亦称“基学习器”。集成学习通过将多个学习器进行结合,常可获得比单一学习器显著优越的泛化性能。根据个体学习器的生成方式,目前的集成学习方法大致可分为两大类,即个体学习器间存在强依赖关系、必须串行生成的序列化方法,以及个体学习器间不存在强依赖关系、可同时生成的并行化方法;前者的代表是Boosting,后者的代表是Bagging和随机森林。
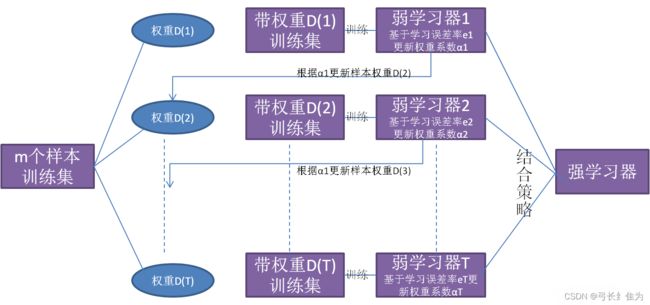
Boosting是一族可将弱学习器提升为强学习器的算法。这族算法的工作机制类似可描述为:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直至基学习器数目达到事先指定的值T,最终将这T个基学习器进行加权结合。
(3)AdaBoost算法设计思路
根据上面的数学推导,已经得出了基学习器的权重更新公式,于是可以得出AdaBoost的算法步骤:
(4)AdaBoost实验流程分析
AdaBoost算法的核心思想是前向分布求解,即每一轮只学习一个弱学习器及它的权重。通俗来讲,AdaBoost算法分为三步:
首先初始化训练数据的权值分布,如果有m个样本,则每一个训练样本最开始时都被赋予相同的权值1/m。
之后训练弱分类器,具体训练过程中,如果某个样本点已经被准确地分类,那么在构造下一个训练集中,它的权重就被降低,而如果某个样本点没有被准确地分类,那么它的权值就得到提高,权值更新过的样本集被用于训练下一个分类器,整个训练过程如此迭代地进行下去。
最后将各个训练得到的弱分类器组合成强分类器,各个弱分类器的训练过程结束后,加大分类误差率小的弱分类器的权重,使其在最终的分类函数中起着较大的决定作用,而降低分类误差率大的弱分类器的权重,使其在最终的分类函数中起着较小的决定作用。
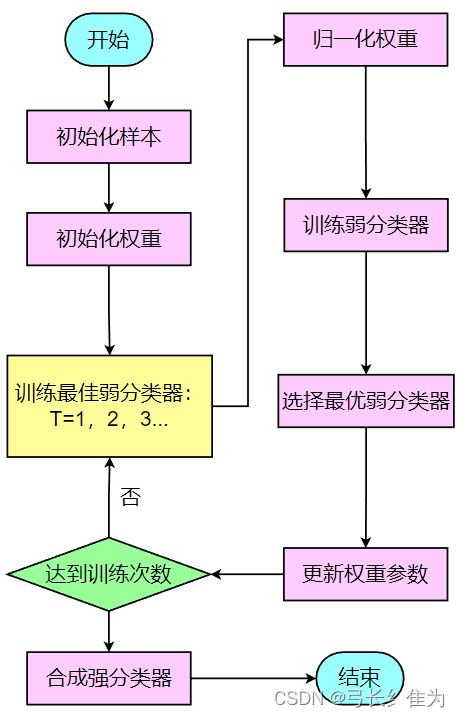
把以上过程绘制成流程图如下:
(5)实验数据的选择(训练集和测试集划分)、实验结果展示、优化与分析
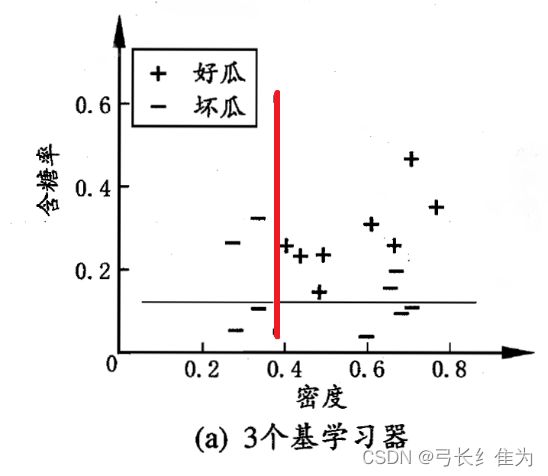
本实验使用的数据集是西瓜数据集3.0,只使用连续型属性。当基学习器数量为3时,我的结果与周志华《机器学习》(西瓜书)对比如下:
前者17个样本预测正确12个,正确率为70.6%;后者17个样本预测正确16个,正确率94.1%。
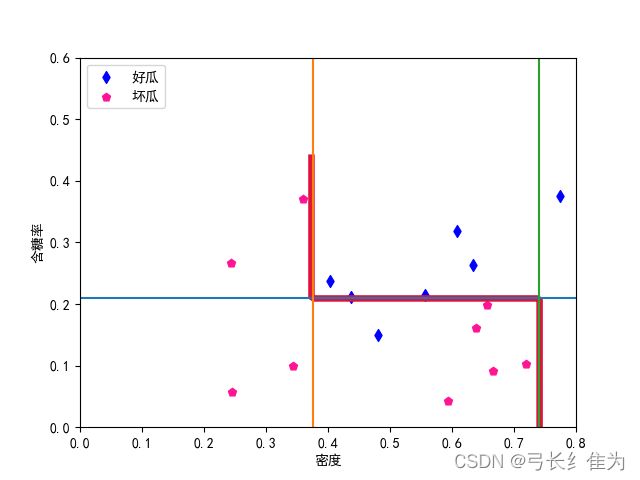
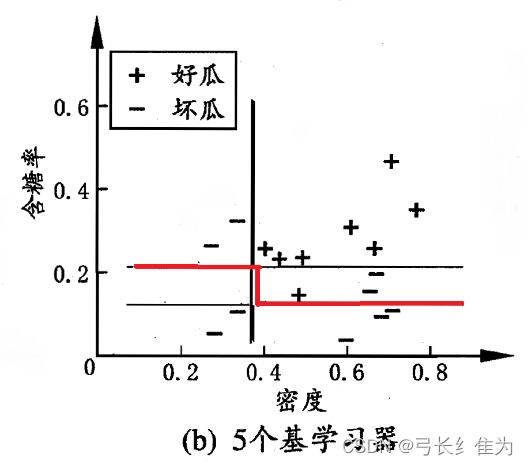
当基学习器数量为5时,我的结果与周志华《机器学习》(西瓜书)对比如下:
前者17个样本预测正确15个,正确率为88.2%;后者17个样本预测正确16个,正确率94.1%。
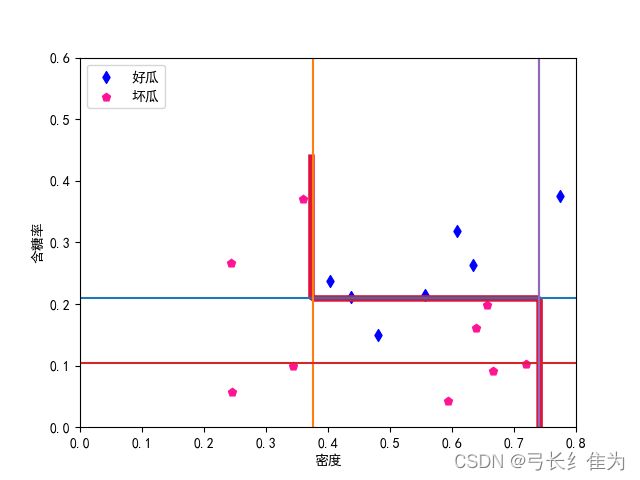
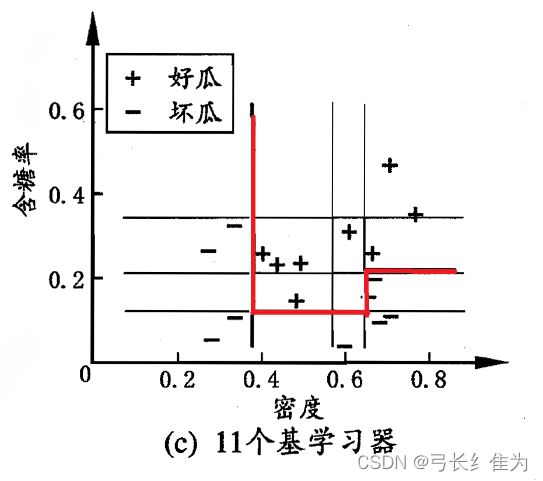
当基学习器数量为11时,我的结果与周志华《机器学习》(西瓜书)对比如下:
前者17个样本预测正确17个,正确率为100%;后者17个样本预测正确17个,正确率100%。
(6)代码结构注释、核心源代码简要分析
本次实验的核心函数就是AdaBoost,其输入为数据集dataSet和基学习器T,输出是保存分类器的字典G和样本权重列表D。它的基本思想是,首先初始化权重,每个样本的初始化权重相同,之后对每一个分类器都根据样本权重D建立决策树桩,并根据其错误率确定该学习器在总学习器中的权重(正确率越高,权重越大)和调整训练样本的权重(被该学习器错误分类的数据提高权重,正确分类的降低权重)。
def AdaBoost(dataSet, T):
m, n = dataSet.shape # 17,3
D = np.ones((1, m)) / m 。
classLabel = dataSet[:, -1].reshape(1, -1) # 数据的类标签。
G = {} # 保存分类器的字典
H=[]
for t in range(T):
stump ,h= buildStump(dataSet, D)
err = stump["err"]
H.append(h)
alpha = np.log((1 - err) / err) / 2 # 第t个分类器的权值
# 更新训练数据集的权值分布
pre = np.zeros((1, m))
for i in range(m):
pre[0][i] = predict(dataSet[i], stump)
a = np.exp(-alpha * classLabel * pre)
D = D * a / np.dot(D, a.T)
G[t] = {}
G[t]["alpha"] = alpha
G[t]["stump"] = stump
H = np.array(H)
return G,H,D
buildStump函数用于建立错误率最小的决策树桩,其基本思想就是对每个特征下的数值,以一定的步长进行遍历(取决于设置的步数),对比移动到哪个位置的时候错误率最低,于是就能得到该数据集下的最优单层决策树。
def buildStump(dataSet, D):
m, n = dataSet.shape # (17,3)
bestErr = np.inf
bestStump = {}
h=[]
numSteps = 16.0 # 每个特征迭代的总步数
for i in range(n-1): # 对第i个特征
rangeMin = dataSet[:, i].min()
rangeMax = dataSet[:, i].max() # 每个属性列的最大最小值
stepSize = (rangeMax - rangeMin) / numSteps # 每一步的长度
for j in range(m): # 对第j个样本
threVal = rangeMin + float(j) * stepSize # 每一步划分的阈值
for inequal in ['lt', 'gt']: # 对于大于或等于符号划分。
err = calErr(dataSet, i, threVal, inequal, D) # 错误率
if err < bestErr: # 如果错误更低,保存划分信息。
bestErr = err
bestStump["feature"] = i
bestStump["threshVal"] = threVal
bestStump["inequal"] = inequal
bestStump["err"] = err
h.append(bestStump["feature"])
h.append(bestStump["threshVal"])
if bestStump["inequal"]=='lt':
h.append(-1)
h.append(1)
if bestStump["inequal"]=='gt':
h.append(1)
h.append(-1)
return bestStump,h
(7)本次实验解决的主要问题、在理论学习与动手编程上的主要收获
要想顺利完成本次实验,必须深入理解AdaBoost算法的步骤及集成思想。AdaBoost算法可分为3个步骤,首先初始化训练数据的权值分布,每一个训练样本最开始时,都会被赋予相同的权值;之后训练弱分类器,如果某个训练样本点,被弱分类器准确地分类,那么再构造下一个训练集中,它对应的权值要减小,而如果某个训练样本点被错误分类,那么它的权值就应该增大,权值的更新过的样本被用于训练下一个弱分类器,整个过程如此迭代下去;
最后,将各个训练得到的弱分类器组合成一个强分类器。各个弱分类器的训练过程结束后,加大分类误差率小的弱分类器的权重,使其在最终的分类函数中起着较大的决定作用,而降低分类误差率大的弱分类器的权重,使其在最终的分类函数中起着较小的决定作用。
通过本次实验,我认识到AdaBoost提供了一种框架,在框架内可以使用各种方法构建子分类器,可以使用简单的弱分类器,不用对特征进行筛选,也不存在过拟合的现象。同时AdaBoost算法不需要弱分类器的先验知识,最后得到的强分类器的分类精度依赖于所有弱分类器。无论是应用于人造数据还是真实数据,AdaBoost都能显著的提高学习精度。另外AdaBoost算法不需要预先知道弱分类器的错误率上限,且最后得到的强分类器的分类精度依赖于所有弱分类器的分类精度,可以深挖分类器的能力。最后,AdaBoost可以根据弱分类器的反馈,自适应地调整假定的错误率,执行的效率高。但不能忽视的是,在训练过程中,AdaBoost会使得难于分类样本的权值呈指数增长,训练将会过于偏向这类困难的样本,导致AdaBoost算法易受噪声干扰。此外,AdaBoost依赖于弱分类器,而弱分类器的训练时间往往很长。
完整代码:
# coding=utf-8
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from numpy import linspace
def getWatermelonDataSet():
"""
西瓜数据集3.0alpha。 列:[密度,含糖量,好瓜]
:return: np数组。
"""
data = pd.read_csv('D:\学习\专业主干课\机器学习\数据集\\watermalon3.0a.csv')
data=np.array(data)
label=data[:,-1]
return data,label
def getUCIDataSet():
data=pd.read_excel('D:\学习\专业主干课\机器学习\数据集\\UCI数据集\\iris.xlsx')
data=np.array(data)
label=data[:,-1]
return data,label
def calErr(dataSet, feature, threshVal, inequal, D):
"""
计算数据带权值的错误率。
:param dataSet: [密度,含糖量,好瓜]
:param feature: [密度,含糖量]
:param threshVal:
:param inequal: 'lt' or 'gt. (大于或小于)
:param D: 数据的权重。错误分类的数据权重会大。
:return: 错误率。
"""
DFlatten = D.flatten() # 变为一维
#print(DFlatten)
errCnt = 0
i = 0
if inequal == 'lt': #如果认为低于阈值为好瓜
for data in dataSet:
if (data[feature] <= threshVal and data[-1] == -1) or \
(data[feature] > threshVal and data[-1] == 1): #则错误判断 = 低于阈值且为坏瓜 + 高于阈值且为好瓜
errCnt += 1 * DFlatten[i] #该样本的权重作为错误率
i += 1
else:
for data in dataSet:
if (data[feature] >= threshVal and data[-1] == -1) or \
(data[feature] < threshVal and data[-1] == 1):
errCnt += 1 * DFlatten[i]
i += 1
return errCnt
def buildStump(dataSet, D):
"""
通过带权重的数据,建立错误率最小的决策树桩。
"""
m, n = dataSet.shape # (17,3)
bestErr = np.inf
bestStump = {}
h=[]
numSteps = 16.0 # 每个特征迭代的总步数
for i in range(n-1): # 对第i个特征
rangeMin = dataSet[:, i].min()
rangeMax = dataSet[:, i].max() # 每个属性列的最大最小值
stepSize = (rangeMax - rangeMin) / numSteps # 每一步的长度
for j in range(m): # 对第j个样本
threVal = rangeMin + float(j) * stepSize # 每一步划分的阈值
for inequal in ['lt', 'gt']: # 对于大于或等于符号划分。
err = calErr(dataSet, i, threVal, inequal, D) # 错误率
if err < bestErr: # 如果错误更低,保存划分信息。
bestErr = err
bestStump["feature"] = i
bestStump["threshVal"] = threVal
bestStump["inequal"] = inequal
bestStump["err"] = err
h.append(bestStump["feature"])
h.append(bestStump["threshVal"])
if bestStump["inequal"]=='lt':
h.append(-1)
h.append(1)
if bestStump["inequal"]=='gt':
h.append(1)
h.append(-1)
#print(h)
return bestStump,h
def predict(data, bestStump):
"""
通过决策树桩预测数据
:param data: 待预测数据
:param bestStump: 决策树桩。
:return:
"""
if bestStump["inequal"] == 'lt':
if data[bestStump["feature"]] <= bestStump["threshVal"]:
return 1
else:
return -1
else:
if data[bestStump["feature"]] >= bestStump["threshVal"]:
return 1
else:
return -1
def AdaBoost(dataSet, T):
"""
每学到一个学习器,根据其错误率确定两件事。
1.确定该学习器在总学习器中的权重。正确率越高,权重越大。
2.调整训练样本的权重。被该学习器误分类的数据提高权重,正确的降低权重,
目的是在下一轮中重点关注被误分的数据,以得到更好的效果。
:param dataSet: 数据集。
:param T: 迭代次数,即训练多少个分类器
:return: 字典,包含了T个分类器。
"""
m, n = dataSet.shape # 17,3
D = np.ones((1, m)) / m # 初始化权重,每个样本的初始权重是相同的。
classLabel = dataSet[:, -1].reshape(1, -1) # 数据的类标签。
G = {} # 保存分类器的字典,
H=[]
for t in range(T): # 对每一个分类器
stump ,h= buildStump(dataSet, D) # 根据样本权重D建立一个决策树桩
err = stump["err"]
H.append(h)
alpha = np.log((1 - err) / err) / 2 # 第t个分类器的权值
# 更新训练数据集的权值分布
pre = np.zeros((1, m))
for i in range(m):
pre[0][i] = predict(dataSet[i], stump)
a = np.exp(-alpha * classLabel * pre)
D = D * a / np.dot(D, a.T)
G[t] = {}
G[t]["alpha"] = alpha
G[t]["stump"] = stump
H = np.array(H)
print(H)
return G,H,D
def adaPredic(data, G):
"""
通过Adaboost得到的总的分类器来进行分类。
:param data: 待分类数据。
:param G: 字典,包含了多个决策树桩
:return: 预测值
"""
score = 0
for key in G.keys():
pre = predict(data, G[key]["stump"]) #每个基分类器的预测结果
score += G[key]["alpha"] * pre #加权结合后的集成预测结果
flag = 0
if score > 0:
flag = 1
else:
flag = -1
return flag
def plotROC(pred_strengths, class_labels):
print(pred_strengths)
# AUC,曲线下的面积
import matplotlib.pyplot as plt
cur = (1.0, 1.0) # cursor # 起始点
y_sum = 0.0 # variable to calculate AUC
num_pos_clas = sum(np.array(class_labels) == 1) # 正例的数目
# 这两个是步长
y_step = 1 / float(num_pos_clas)
x_step = 1 / float(len(class_labels) - num_pos_clas)
# 从小到大排列,再得到下标
sorted_indicies = pred_strengths.argsort() # get sorted index, it's reverse
fig = plt.figure()
fig.clf() # 清空
ax = plt.subplot(111)
# loop through all the values, drawing a line segment at each point
for index in sorted_indicies.tolist()[0]: # np对象变成list
if class_labels[index] == 1.0:
del_x = 0
del_y = y_step
else:
del_x = x_step
del_y = 0
y_sum += cur[1]
# draw line from cur to (cur[0]-delX,cur[1]-delY)
ax.plot([cur[0], cur[0] - del_x], [cur[1], cur[1] - del_y], c='b')
cur = (cur[0] - del_x, cur[1] - del_y)
ax.plot([0, 1], [0, 1], 'b--')
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC curve for AdaBoost horse colic detection system')
ax.axis([0, 1, 0, 1])
plt.show()
print("the Area Under the Curve is: ", y_sum * x_step)
def calcAcc(dataSet, G):
"""
计算准确度
:param dataSet: 数据集
:param G: 字典,包含了多个决策树桩
:return:
"""
rightCnt = 0
for data in dataSet:
pre = adaPredic(data, G)
if pre == data[-1]:
rightCnt += 1
return rightCnt / float(len(dataSet))
def predictt(H, X1, X2):
# 预测结果
# 仅X1和X2两个特征,X1和X2同维度
pre = np.zeros(X1.shape)
for h in H:
df, t, lv, rv = h # 划分特征,划分点,左枝取值,右枝取值
X = X1 if df == 0 else X2
pre += (X <= t) * lv + (X > t) * rv
return np.sign(pre)
# 绘制数据集,clf为获得的集成学习器
def plotData(data, clf,H,t):
xx1min, xx1max = data[:, 0].min(), data[:, 0].max()
xx2min, xx2max = data[:, 1].min(), data[:, 1].max()
xx1 = np.linspace(xx1min - (xx1max - xx1min) * 0.2, xx1max + (xx1max - xx1min) * 0.2, 100)
xx2 = np.linspace(xx2min - (xx2max - xx2min) * 0.2, xx2max + (xx2max - xx2min) * 0.2, 100)
XX1, XX2 = np.meshgrid(xx1, xx2)
Ypre = predictt(H[:t], XX1, XX2)
plt.contour(XX1, XX2, Ypre, colors='crimson', linewidths=4.7, levels=[0])
X1, X2 = [], []
Y1, Y2 = [], []
datas=data
labels=data[:,2]
for data, label in zip(datas, labels):
if label > 0:
X1.append(data[0])
Y1.append(data[1])
else:
X2.append(data[0])
Y2.append(data[1])
x = linspace(0, 0.8, 100)
y = linspace(0, 0.6, 100)
for key in clf.keys():
z = [clf[key]["stump"]["threshVal"]]*100
if clf[key]["stump"]["feature"] == 0:
plt.plot(z, y)
else:
plt.plot(x, z)
plt.scatter(X1, Y1, marker='d', label='好瓜', color='b')
plt.scatter(X2, Y2, marker='p', label='坏瓜', color='deeppink')
plt.xlabel('密度')
plt.ylabel('含糖率')
plt.xlim(0, 0.8) # 设置x轴范围
plt.ylim(0, 0.6) # 设置y轴范围
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.legend(loc='upper left')
plt.show()
def main():
dataSet ,label = getWatermelonDataSet()
#dataSet,label=getUCIDataSet()
for t in [3, 5, 11]: # 学习器的数量
G,H,D= AdaBoost(dataSet, t)
print('集成学习器(字典):',f"G{t} = {G}")
print('准确率=',calcAcc(dataSet, G))
#绘图函数
plotData(dataSet,G,H,t)
#plotROC(D,label)
if __name__ == '__main__':
main()