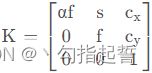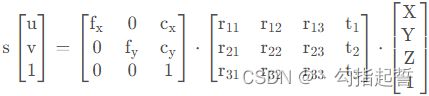第四章 照相机模型与增强现实
一、针孔照相机模型
针孔照相机模型(有时称为射影照相机模型)是计算机视觉中广泛使用的照相机模型。对于大多数应用来说,针孔照相机模型简单,并且具有足够的精确度。这个名字源于一种类似暗箱机的照相机,该照相机从一个小孔采集射到暗箱内部的光线,如图所示。
比较基础简单的投影变换有正交变换和透视变换。正交变换就是物体上的点全都平行地投射到投影面,没有远近的区别,即没有透视效果。 透视变换正好相反,被投影物体处于一个四棱台区域中,物体被投影到离相机较近的平面上。相机被抽象为一个点,而投影点是物体上的点和相机的连线与投影平面的交点。由于投影的路径不再相互平行,因此会产生透视效果。
1、照相机矩阵
照相机矩阵可分解为:P=K[R∣t],其中R是描述照相机方向的旋转矩阵,t是描述照相机中心位置的三维平移向量,内标定矩阵K描述照相机的投影性质。
平面和照相机中心间的距离为焦距f。当像素数组在传感器上偏斜的时候,需要用到倾斜参数s。在大多数情况下,s可以设置为0,那样上述公式可以写成: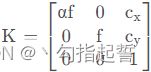
2、三维点的投影
首先创建照相机类,用来处理对照相机和投影建模所需要的全部操作代码:
from scipy import linalg
class Camera(object):
"""表示针孔照相机的类"""
def __init__(self,P): #注意:需要左右各需要两个下划线
"""初始化P=K[R|t]照相机模型"""
self.P = P
self.K = None #标定矩阵
self.R = None #旋转
self.t = None #平移
self.c = None #照相机中心
def project(self,X):
"""X(4*n的数组)的投影点,并且进行坐标归一化"""
x = dot(self.P,X)
for i in range(3):
x[i]/=x[2]
return x
#该函数是一种矩阵因子分解方法,称为RQ因子分解。其结果不是唯一的,结果存在符号二义性。
def factor(self):
"""将照相机矩阵分解为K、R、t,其中,P=K[R|t]"""
#分解前3*3的部分
K,R = linalg.rq(self.P[:,:,3])
#将K的对角线元素设为正值
T = diag(sign(diag(K)))
if linalg.det(T) < 0:
T[1,1]*=-1
self.K = dot(K,T)
self.R = dot(T,R) #T的逆矩阵为其自身
self.t = dot(linalg.inv(self.K),self.P[:,3])
return self.K,self.R,self.t
#计算照相机的中心
def center(self):
"""计算并返回照相机的中心"""
if self.c is not None:
return self.c
else:
#通过因子分解计算c
self.factor()
self.c = -dot(self.R.T,self.t)
return self.c
3、照相机矩阵的分解
简化公式为:s ⋅ m ′ = A ⋅ [ R ∣ t ] ⋅ M ′
其中m ′ 为屏幕uv坐标,A为相机内参,[ R ∣ t ] 为相机外参,M ′ 为物体世界坐标,而s为物体在相机坐标系中的z坐标,这是公式推导过程中产生的参数。这里提到的相机内参是指仅由相机本身决定的参数,也就是对某一相机一旦这个值算好就不用再次进行计算。相对的,外参是和世界坐标系和相机位置有关的。
照相机模型是属于计算机3D视觉中的,而所谓3D视觉就是要建立二维图像和三维场景的联系,比较主要的一个用途是根据二维图片重建三维场景。所以一个自然的想法就是通过各种方式使得可以从三维坐标计算得到屏幕空间坐标或者相反。
二、照相机标定
简单来说就是从世界坐标系换到图像坐标系的过程,也就是求最终的投影矩阵P的过程。
原理:一般来说,标定的过程分为两个部分
1、从世界坐标系转换为相机坐标系,这一步是三维点到三维点的转换,包括 R ,t (相机外参)等参数。
2、从相机坐标系转为图像坐标系,这一步是三维点到二维点的转换,包括 K(相机内参)等参数。
步骤:
- 打印一张棋盘格,把它贴在一个平面上,作为标定物。
- 通过调整标定物或摄像机的方向,为标定物拍摄一些不同方向的照片。
- 从照片中提取棋盘格角点。
- 估算理想无畸变的情况下,五个内参和六个外参。
- 应用最小二乘法估算实际存在径向畸变下的畸变系数。
- 极大似然估计法,优化估计,提升估计精度。
三、增强现实(AR)
增强现实是将物体和相应信息放置在图像数据上的一系列操作的总称。需要用到两个工具包,分别是:PyGame和PyOpenGL。
1、PyGame和PyOpenGL
pygame可直接使用pip install命令安装,pip install PyGame 。
但PyOpenGL默认安装32位,我们要手动下载64位下载地址然后在下载位置使用pip install (文件名.whl)进行安装。pip install PyOpenGL-3.1.3b2-cp37-cp37m-win_amd64.whl 进行下载,这个根据自己的情况来进行调整。我所使用的电脑是win10,64位,使用的版本是Python3.7。
为了使用上面两个工具包,需要在脚本的开始部分载入下面的命令:
from OpenGL.GL import *
from OpenGL.GLU import *
import pygame, pygame.image
from pygame.locals import *
2、从照相机矩阵到OpenGL格式
openGL使用4×4的矩阵来表示变换。但是照相机与场景的变换分成了两个矩阵,GL_PROJECTION矩阵和GL_MODELVIEW矩阵。GL_PROJECTION矩阵处理图像成像的性质,等价于我们的内标定矩阵K 。GL_MODELVIEW矩阵处理物体和照相机之间的三维变换关系,对应于我们照相机矩阵中的R 和t 部分。
3、在图像中放置虚拟物体
在OpenGL中,该操作可以通过创建一个四边形的方式来完成,该四边形为整个视图。完成该操作最简单的方式是绘制出四边形,同时将投影和模拟视图矩阵重置,使得每一维的坐标范围在-1到1之间。
注:最近几天不知道电脑还是网页怎么回事,CSDN的公式编辑用不了,没法自己编辑公式了。只能用截图的方式,望谅解。