吴恩达深度学习：正交化、单一数字评估、满足优化指标

此公众号会发表计算机考研（初复试信息）、夏令营等资料，方便考研人对信息的获取，节约自身查找资料的时间

目录

正交化

单一数字评估指标

满足和优化指标 (Satisficing and Optimizing Metrics)

---

正交化

搭建建立机器学习系统的挑战之一是，你可以尝试和改变的东西太多太多了。包括，比如说，有那么多的超参数可以调。我留意到，那些效率很高的机器学习专家有个特点，他们思维清晰，对于要调整什么来达到某个效果，非常清楚，这个步骤我们称之为正交化，让我告诉你是什么意思吧。

这是一张老式电视图片，有很多旋钮可以用来调整图像的各种性质，所以对于这些旧式电视，可能有一个旋钮用来调图像垂直方向的高度，另外有一个旋钮用来调图像宽度，也许还有一个旋钮用来调梯形角度，还有一个旋钮用来调整图像左右偏移，还有一个旋钮用来调图像旋转角度之类的。电视设计师花了大量时间设计电路，那时通常都是模拟电路来确保每个旋钮都有相对明确的功能。如一个旋钮来调整这个（高度），一个旋钮调整这个（宽度），一个旋钮调整这个（梯形角度），以此类推。

相比之下，想象一下，如果你有一个旋钮调的是 0.1 x 0.1x 0.1x 表示图像高度， + 0.3 x +0.3x +0.3x 表示图像宽度， − 1.7 x -1.7x −1.7x 表示梯形角度， + 0.8 x +0.8x +0.8x 表示图像在水平轴上的坐标之类的。如果你调整这个（其中一个）旋钮，那么图像的高度、宽度、梯形角度、平移位置全部都会同时改变，如果你有这样的旋钮，那几乎不可能把电视调好，让图像显示在区域正中。

所以在这种情况下，正交化指的是电视设计师设计这样的旋钮，使得每个旋钮都只调整一个性质，这样调整电视图像就容易得多，就可以把图像调到正中。

正交化就是对机器学习算法的调整，当算法在某方面有问题时，设定相对应的方法解决调整

单一数字评估指标

无论你是调整超参数，或者是尝试不同的学习算法，或者在搭建机器学习系统时尝试不同手段，你会发现，如果你有一个单实数评估指标，你的进展会快得多，它可以快速告诉你，新尝试的手段比之前的手段好还是差。所以当团队开始进行机器学习项目时，我经常推荐他们为问题设置一个单实数评估指标。

我们来看一个例子，你之前听过我说过，应用机器学习是一个非常经验性的过程，我们通常有一个想法，编程序，跑实验，看看效果如何，然后使用这些实验结果来改善你的想法，然后继续走这个循环，不断改进你的算法。

比如说对于你的猫分类器，之前你搭建了某个分类器 A A A ，通过改变超参数，还有改变训练集等手段，你现在训练出来了一个新的分类器B，所以评估你的分类器的一个合理方式是观察它的查准率（precision）和查全率（recall）。

查准率和查全率的确切细节对于这个例子来说不太重要。但简而言之，查准率的定义是在你的分类器标记为猫的例子中，有多少真的是猫。所以如果分类器 A A A 有95%的查准率，这意味着你的分类器说这图有猫的时候，有95%的机会真的是猫。

查全率就是，对于所有真猫的图片，你的分类器正确识别出了多少百分比。实际为猫的图片中，有多少被系统识别出来？如果分类器 A A A 查全率是90%，这意味着对于所有的图像，比如说你的开发集都是真的猫图，分类器 A A A 准确地分辨出了其中的90%。

所以关于查准率和查全率的定义，不用想太多。事实证明，查准率和查全率之间往往需要折衷，两个指标都要顾及到。你希望得到的效果是，当你的分类器说某个东西是猫的时候，有很大的机会它真的是一只猫，但对于所有是猫的图片，你也希望系统能够将大部分分类为猫，所以用查准率和查全率来评估分类器是比较合理的。

但使用查准率和查全率作为评估指标的时候，有个问题，如果分类器 A A A 在查全率上表现更好，分类器 B B B 在查准率上表现更好，你就无法判断哪个分类器更好。如果你尝试了很多不同想法，很多不同的超参数，你希望能够快速试验不仅仅是两个分类器，也许是十几个分类器，快速选出“最好的”那个，这样你可以从那里出发再迭代。如果有两个评估指标，就很难去快速地二中选一或者十中选一，所以我并不推荐使用两个评估指标，查准率和查全率来选择一个分类器。你只需要找到一个新的评估指标，能够结合查准率和查全率。

在机器学习文献中，结合查准率和查全率的标准方法是所谓的 F 1 F_1 F1​ 分数， F 1 F_1 F1​ 分数的细节并不重要。但非正式的，你可以认为这是查准率 P P P 和查全率 R R R 的平均值。正式来看， F 1 F_1 F1​ 分数的定义是这个公式： 2 1 P + 1 R \frac2{\frac1P+\frac1R} P1​+R1​2​

在数学中，这个函数叫做查准率 P P P 和查全率 R R R 的调和平均数。但非正式来说，你可以将它看成是某种查准率和查全率的平均值，只不过你算的不是直接的算术平均，而是用这个公式定义的调和平均。这个指标在权衡查准率和查全率时有一些优势。

但在这个例子中，你可以马上看出，分类器 A A A 的 F 1 F_1 F1​ 分数更高。假设分数是结合查准率和查全率的合理方式，你可以快速选出分类器 A A A ，淘汰分类器 B B B 。

我发现很多机器学习团队就是这样，有一个定义明确的开发集用来测量查准率和查全率，再加上这样一个单一数值评估指标，有时我叫单实数评估指标，能让你快速判断分类器 A A A 或者分类器 B B B 更好。所以有这样一个开发集，加上单实数评估指标，你的迭代速度肯定会很快，它可以加速改进您的机器学习算法的迭代过程。

也就是说，当有多个评估指标对算法就行评估时，有时候很难从多个评估指标中选择一个好的算法，这时候可以将多个评估指标融合成一个单一数字评估指标，从而可以简化对算法的选择

满足和优化指标 (Satisficing and Optimizing Metrics)

要把你顾及到的所有事情组合成单实数评估指标有时并不容易，在那些情况里，我发现有时候设立满足和优化指标是很重要的，让我告诉你是什么意思吧。

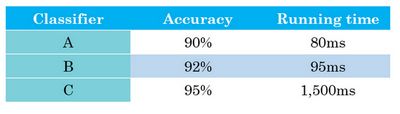
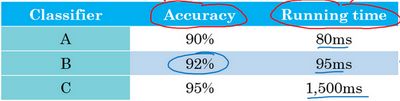
假设你已经决定你很看重猫分类器的分类准确度，这可以是 F 1 F_1 F1​ 分数或者用其他衡量准确度的指标。但除了准确度之外，我们还需要考虑运行时间，就是需要多长时间来分类一张图。分类器 A A A 需要80毫秒， B B B 需要95毫秒， C C C 需要1500毫秒，就是说需要1.5秒来分类图像。

你可以这么做，将准确度和运行时间组合成一个整体评估指标。所以成本，比如说，总体成本是 c o s t = a c c u r a c y − 0.5 ∗ r u n n i n g T i m e cost=accuracy-0.5*runningTime cost=accuracy−0.5∗runningTime ，这种组合方式可能太刻意，只用这样的公式来组合准确度和运行时间，两个数值的线性加权求和。

你还可以做其他事情，就是你可能选择一个分类器，能够最大限度提高准确度，但必须满足运行时间要求，就是对图像进行分类所需的时间必须小于等于100毫秒。所以在这种情况下，我们就说准确度是一个优化指标，因为你想要准确度最大化，你想做的尽可能准确，但是运行时间就是我们所说的满足指标，意思是它必须足够好，它只需要小于100毫秒，达到之后，你不在乎这指标有多好，或者至少你不会那么在乎。所以这是一个相当合理的权衡方式，或者说将准确度和运行时间结合起来的方式。实际情况可能是，只要运行时间少于100毫秒，你的用户就不会在乎运行时间是100毫秒还是50毫秒，甚至更快。

通过定义优化和满足指标，就可以给你提供一个明确的方式，去选择“最好的”分类器。在这种情况下分类器B最好，因为在所有的运行时间都小于100毫秒的分类器中，它的准确度最好。

所以更一般地说，如果你要考虑 N N N 个指标，有时候选择其中一个指标做为优化指标是合理的。所以你想尽量优化那个指标，然后剩下 N − 1 N-1 N−1 个指标都是满足指标，意味着只要它们达到一定阈值，例如运行时间快于100毫秒，但只要达到一定的阈值，你不在乎它超过那个门槛之后的表现，但它们必须达到这个门槛。

总结：有时候想让多个评估指标融合成为一个单一数字评估指标有难度，或者说不可能，这时候就可以用以上方法，设定满足指标和优化指标，即设定一个指标为优化指标（尽可能的去优化），其余指标为满足指标，满足指标只要到满足某个至即可，比如说只要算法的运行时间都小于100秒即可，从而选择准确率高的算法