pytorch基础数据类型--tensor

一. 创建tensor

tensor类似于numpy的ndarray, 很多操作方法也相似

import torch
import numpy as np

# 使用python列表创建tensor
data = [[1, 2], [3, 4]]
# 总是发生拷贝
x_data = torch.tensor(data)
print(x_data)

# 使用ndarray创建tensor
np_array = np.array(data)
# 共享底层存储
x_np = torch.from_numpy(np_array)
print(x_np)

# 创建相同形状的值全为1的tensor
x_ones = torch.ones_like(x_data)
print(x_ones)

# 创建相同形状的值为随机数的tensor
x_rand = torch.rand_like(x_data, dtype=torch.float)
print(x_rand)

# 创建固定形状值为固定值或随机值的tensor
shape = (2,3,)
rand_tensor = torch.rand(shape)
ones_tensor = torch.ones(shape)
zeros_tensor = torch.zeros(shape)

二. tensor属性

1. 判断属性

is_cuda 是否存储在GPU上

is_quantized

is_meta

2. 基本属性

dtype 数据类型

Data type	dtype	Legacy Constructors
32-bit floating point	torch.float32 or torch.float	torch.*.FloatTensor
64-bit floating point	torch.float64 or torch.double	torch.*.DoubleTensor
64-bit complex	torch.complex64 or torch.cfloat
128-bit complex	torch.complex128 or torch.cdouble
16-bit floating point 1	torch.float16 or torch.half	torch.*.HalfTensor
16-bit floating point 2	torch.bfloat16	torch.*.BFloat16Tensor
8-bit integer (unsigned)	torch.uint8	torch.*.ByteTensor
8-bit integer (signed)	torch.int8	torch.*.CharTensor
16-bit integer (signed)	torch.int16 or torch.short	torch.*.ShortTensor
32-bit integer (signed)	torch.int32 or torch.int	torch.*.IntTensor
64-bit integer (signed)	torch.int64 or torch.long	torch.*.LongTensor
Boolean	torch.bool	torch.*.BoolTensor

device 计算引擎

shape 形状

3. 操作

T 转置

real 返回复数实部的新tensor

共享底层存储

imag 返回复数虚部的新tensor

共享底层存储

4. 其它

grad 梯度

ndim

三. tensor方法

1. 构造新tensor

默认使用旧tensor的dtype和device创建一个新tensor
此处罗列共同参数, 下方不再赘述

参数名	默认值	说明
dtype	None	指定生成的tensor的数据类型
device	None	指定计算引擎
requires_grad	False	是否允许反向传播

requires_grad没懂先引用

new_tensor 创建新tensor

参数名	默认值	说明
data	-	源数据, 且新生成的tensor总是发生数据拷贝

new_full 创建指定形状指定值的tensor

参数名	默认值	说明
size	-	形状
fill_value	-	值

new_empty 创建指定形状的空tensor

默认会有值填充但其值没有实际含义

参数名	默认值	说明
size	-	形状

new_ones 创建指定形状值为1的tensor

参数名	默认值	说明
size	-	形状

2. 数学函数

_ 结尾的函数会共享底层存储

abs, abs_, absolute, absolute_ 绝对值

add, add_ 求和

$out=input+\alpha other$

参数名	默认值	说明
other	-	可以是数字或tensor等
alpha	1	other的权重

addcdiv, addcdiv_ $ou{t}_i=inpu{t}_i+value\times \frac{tensor{1}_i}{tensor{2}_i}$

$$ou{t}_i=inpu{t}_i+value\times \frac{tensor{1}_i}{tensor{2}_i}$$

参数名	默认值	说明
tensor1	-
tensor2	-
value	1

addcmul, addcmul_ $ou{t}_i=inpu{t}_i+value\times tensor{1}_i\times tensor{2}_i$

$$ou{t}_i=inpu{t}_i+value\times tensor{1}_i\times tensor{2}_i$$

参数名	默认值	说明
tensor1	-
tensor2	-
value	1

addbmm, addbmm_ $\beta input+\alpha ({\sum }_{i=0}^{b-1}batch{1}_i@batch{2}_i)$ ¹

input.shape => $(n\ast p){}_{input即当前tensor}$
out.shape => $(n\ast p)$
$$\beta input+\alpha (\sum _{i=0}^{b-1}batch{1}_i@batch{2}_i)$$

参数名	默认值	说明
batch1	-	形状 $(b\ast n\ast m)$
batch2	-	形状 $(b\ast m\ast p)$
beta	1	$\beta$
alpha	1	$\alpha$

baddbmm, baddbmm_ $ou{t}_i=\beta inpu{t}_i+\alpha (batch{1}_i@batch{2}_i)$

input.shape => $(b\ast n\ast p){}_{input即当前tensor}$
out.shape => $(b\ast n\ast p)$
$$ou{t}_i=\beta inpu{t}_i+\alpha (batch{1}_i@batch{2}_i)$$

参数名	默认值	说明
batch1	-	形状 $(b\ast n\ast m)$
batch2	-	形状 $(b\ast m\ast p)$
beta	1	$\beta$
alpha	1	$\alpha$

addmm, addmm_, sspaddmm $\beta input+\alpha (mat1@mat2)$ ¹

input.shape => $(n\ast p){}_{input即当前tensor}$
out.shape => $(n\ast p)$
$$out=\beta input+\alpha (mat1@mat2)$$

参数名	默认值	说明
mat1	-	形状 $(n\ast m)$
mat2	-	形状 $(m\ast p)$
beta	1	$\beta$
alpha	1	$\alpha$

addmv, addmv_ $\beta input+\alpha (mat@vec)$ ¹

input.shape => $(n,){}_{input即当前tensor}$
out.shape => $(n,)$
$$out=\beta input+\alpha (mat@vec)$$

参数名	默认值	说明
mat	-	形状 $(n,m)$
vec	-	形状 $(m,)$ 一维, 进行矩阵运算时转为 (m, 1)
beta	1	$\beta$
alpha	1	$\alpha$

addr, addr_ $out=\beta input+\alpha (vec1\otimes vec2)$ ²

input.shape => $(n,m){}_{input即当前tensor}$
out.shape => $(n,m)$
$$out=\beta input+\alpha (vec1\otimes vec2)$$

参数名	默认值	说明
vec1	-	形状 $(n,)$ 运算时转为 (n, 1)
vec2	-	形状 $(m,)$ 原酸时转为 (1, m)
beta	1	$\beta$
alpha	1	$\alpha$

bernoulli, bernoulli_ 伯努利分布

$$ou{t}_i\sim Bernoulli(p=inpu{t}_i);0\le inpu{t}_i\le 1$$
伯努利分布指的是对于随机变量X有, 参数为p(0

参数名	默认值	说明
generator	-	类似于随机数种子, 同一个种子返回的数据是固定的. 例如: torch.Generator().manual_seed(2)
### allclose $	input - other	\le atol + rtol ×

out => bool
$$|input-other|\le atol+rtol\times |other|$$

参数名	默认值	说明
other	-
rtol	1e-05
atol	1e-08
equal_nan	False	如果为True两个NaN将被视为相等否则视为不相等

all 判断所有元素是否都为True(或非零值)

参数名	默认值	说明
dim	None	缩减的维度
keepdim	False	结果是否保留原维度

any 判断是否包含True(或非零值)

参数名	默认值	说明
dim	None	缩减的维度
keepdim	False	结果是否保留原维度

amax 获取缩减指定维度后的最大值

参数名	默认值	说明
dim	None	缩减的维度, 默认获取全局最大值
keepdim	False	结果是否保留原维度

amin 获取缩减指定维度后的最小值

参数名	默认值	说明
dim	None	缩减的维度, 默认获取全局最小值
keepdim	False	结果是否保留原维度

argmax 获取缩减指定维度后的最大值的索引

参数名	默认值	说明
dim	None	缩减的维度
keepdim	False	结果是否保留原维度

argmin 获取缩减指定维度后的最小值的索引

参数名	默认值	说明
dim	None	缩减的维度
keepdim	False	结果是否保留原维度

argsort 获取排序后值在原数据中的索引位置

参数名	默认值	说明
dim	-1	排序维度, 默认对最后一个维度排序
descending	False	默认升序排序

angle 角度

tensor值为复数

acos, acos_, arccos, arccos_ 反余弦

asin, asin_, arcsin, arcsin_ 反正弦

atan, atan_, arctan, arctan_ 反正切

atan2, atan2_ $ou{t}_i=atan(inpu{t}_i/othe{r}_i)$

$$ou{t}_i=atan(inpu{t}_i/othe{r}_i)$$

参数名	默认值	说明
other	-

backward

参数名	默认值	说明
gradient	None
retain_graph	None
create_graph	False
inputs	None

3. 转换

as_strided 生成视图

参数名	默认值	说明
size	-	输出tensor的形状
stride	-	生成视图时每一个维度的步长
storage_offset	0	偏移量

a = torch.randn(3, 3)
b = torch.as_strided(a, (2, 2, 2), (1, 3, 1), 1)

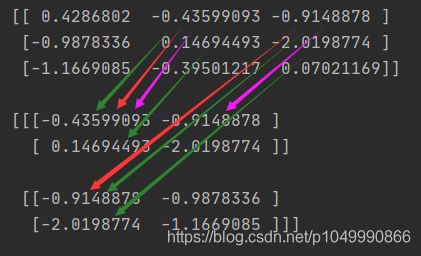
由于示例偏移量是1所以从第二个元素开始生成视图
如图红色是第一个维度, 每隔一个元素取一个值
绿色是第二个维度, 每隔三个元素取一个值
紫色是第三个维度, 每隔一个元素取一个值

bfloat16 将数据类型转换为bfloat16

等同于 self.to(torch.bfloat16)

参数名	默认值	说明
memory_format	torch.preserve_format

4. 其它

apply_ 对每一个元素进行替换

仅适用于CPU处理器
此函数类似于python的map

参数名	默认值	说明
callable	-	输入一个值输出一个值的函数

---

1. $@$ 表示矩阵求积操作 ↩︎ ↩︎ ↩︎

2. $\otimes$ 表示将向量转为矩阵求积, 比如将 $n\otimes m$ 转为 $(n,1)@(1,m)$ ↩︎