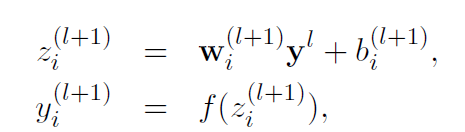Dropout
Dropout: A Simple Way to Prevent Neural Networks from Over tting
1. Introduction
深层神经网络包含多个非线性隐藏层，这使得它们具有很强的表达能力，能够学习输入和输出之间非常复杂的关系然而，在训练数据有限的情况下，这些复杂的关系很多都会是抽样噪声的结果，所以它们会存在于训练集中，但在真实的测试数据中却不存在，即使它是从同一个分布中抽取的。这导致了过拟合，许多方法已经被发明出来减少过拟合的影响。这些措施包括在验证集的性能开始恶化时立即停止训练，引入各种类型的权重惩罚，如L1和L2正则化和soft weight sharing（Nowlan和Hinton，1992）。
模型组合总是能提高机器学习方法的性能。然而，对于大型神经网络，对许多单独训练的网络的输出进行平均的想法明显是非常昂贵的。当单个模型彼此不同时，组合多个模型是最有帮助的，为了使神经网络模型不同，它们要么具有不同的体系结构，要么接受不同数据的训练。 训练许多不同的体系结构是很困难的，因为为每个体系结构找到最优的超参数是一项艰巨的任务，训练每个大型网络需要大量的计算。此外，大型网络通常需要大量的训练数据，而且可能没有足够的数据可用来训练不同网络上不同子集的数据。即使能够训练许多不同的大型网络，在需要快速响应的应用程序中，在测试时使用它们也是不可行的。
Dropout是一种解决这两个问题的技术。它防止了过拟合，并提供了一种有效地近似指数组合多种不同神经网络结构的方法。术语“dropout”是指丢弃一个神经网络中（隐藏和可见）的神经元。通过dropping一个单元，我们的意思是暂时将它以及它的所有输入和输出连接从网络中删除，如图1所示。选择要删除的单元是随机的。在最简单的情况下，每一个单元都以固定的概率p保留，其中p可以使用验证集来选择，也可以简单地设置为0.5，这对于广泛的网络和任务来说似乎接近最优。然而，对于输入单位，最优保留概率通常接近1而不是0.5。
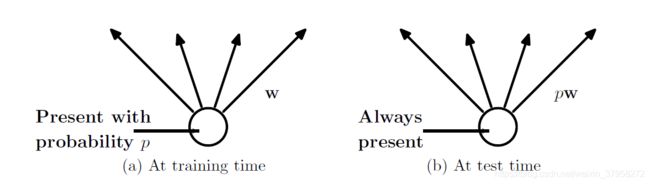
图2：左：训练时的一个单位，它以概率p表示，并用权重w连接到下一层的单位。右：在测试时，该单位始终存在，权重乘以p。测试时的输出与训练时的预期输出相同。
将dropout应用于神经网络相当于从中抽取一个“细化”的网络。细化后的网络由所有从dropout中幸存下来的单元组成（图1b）。一个具有n个单位的神经网络，可以看作是 2 n 2^n 2n个可能的稀疏神经网络的集合。
这些网络都共享权重，因此参数总数仍然是 O ( n 2 ) O(n^2) O(n2)。因此，训练一个dropout的神经网络可以看作是训练一组 2 n 2^n 2n个具有广泛权重共享的细化网络。
在测试时，不可能显式地平均来自指数级的许多细化模型的预测。然而，一个非常简单的近似平均方法在实践中效果良好。这个想法是在测试时使用一个单一的没有dropout的神经网络。如果在训练期间以概率p保留一个单元，则该单元的输出权重在测试时乘以p，如图2所示。通过这种缩放， 2 n 2^n 2n个具有共享权重的网络可以组合成一个单独的神经网络，在测试时使用。我们发现，与其他正则化方法相比，训练一个有dropout的网络，并在测试时使用这种近似平均方法，可以显著降低在各种分类问题上的泛化误差。
dropout并不局限于前馈神经网络。它可以更广泛地应用于图形模型，如Boltzmann机器。本文介绍了dropout受限Boltzmann机器模型，并将其与标准受限Boltzmann机器（RBM）进行了比较。实验结果表明，退学红细胞在某些方面优于标准RBMs。
2. Motivation
dropout的动机来自性别在进化中的作用理论（Livnat等人，2010）。有性生殖是指将父母一方的一半基因和另一方的一半基因，加上极少量的随机突变，并结合起来产生后代。无性繁殖的另一种选择是用父母基因的稍有变异的拷贝创造后代。无性繁殖应该是优化个体适应度的更好方法，这似乎是合理的，因为一组良好的基因可以直接遗传给后代。另一方面，有性生殖可能会破坏这些共同适应的基因集，特别是如果这些基因集很大，直觉上，这会降低已经进化出复杂共同适应的有机体的适应度。然而，有性生殖是最先进的有机体进化的方式。
对有性生殖优越性的一种可能解释是，从长期来看，自然选择的标准可能不是个体适应，而是基因的混合能力。一组基因能够与另一组随机基因很好地协同工作，这使得它们更加健壮。因为一个基因不能依赖于一大群伴侣的存在，所以它必须学会自己做一些有用的事情，或者与少数其他基因合作。根据这一理论，有性生殖的作用不仅是允许有用的新基因在整个种群中传播，而且还通过减少复杂的共适应来促进这一过程，这种共适应会减少新基因改善个体适应能力的机会。类似地，神经网络中的每个隐藏单元都必须学习如何处理随机选择的其他单元样本。这将使每个隐藏单元更加健壮，并促使它自己创建有用的特性，而不依赖其他隐藏单元来纠正错误。然而，一个层中隐藏的单元仍然会学会做不同的事情。
3. Related Work
Dropout可以解释为一种通过在神经网络的隐藏单元中加入噪声来调整神经网络的方法。Vincent等人（2008，2010）在自动编码器的输入单元中添加噪声，并训练网络以重构无噪声输入。 我们的工作扩展了这一概念，表明Dropout可以有效地应用于隐藏层，也可以解释为一种形式的模型平均。我们还证明了加噪不仅对无监督特征学习有用，而且可以推广到有监督学习问题。实际上，我们的方法可以应用到其他基于神经元的体系结构中，例如Boltzmann机。虽然5%的噪声通常对DAE最有效，但我们发现，在测试时应用的权重缩放过程使我们能够使用更高的噪声级别。剔除20%的输入单元和50%的隐藏单元通常被认为是最优的。
4. Model Description
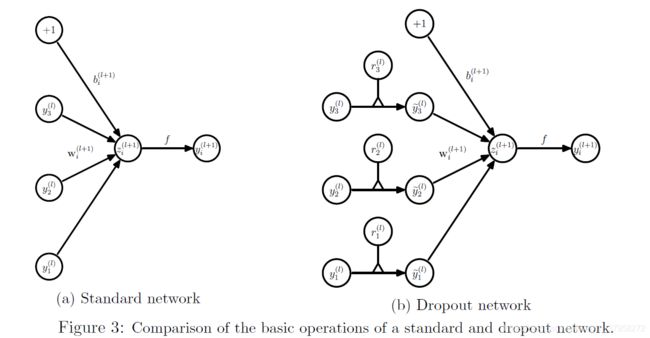
本节介绍了Dropout神经网络模型。考虑一个具有L个隐藏层的神经网络。让 l ∈ { 1 , . . . , L } l\in\{1,...,L\} l∈{1,...,L}为网络隐藏层的索引。让 z ( l ) z^{(l)} z(l)代表第 l 层的输入向量。 y ( l ) y^{(l)} y(l)为第 l 层的输出向量（ y ( 0 ) = x y^{(0)}=x y(0)=x为输入）。 W ( l ) , b ( l ) W^{(l)},b^{(l)} W(l),b(l) 是第 l 层的权重和偏置值。一个标准神经网络的前馈操作(图3a)可以描述为(for l ∈ { 0 , . . . , L − 1 } l\in\{0,...,L-1\} l∈{0,...,L−1})。
f f f 代表任意激活函数，例如， f ( x ) = 1 / 1 ( 1 + e x p ( − x ) ) . f(x)=1/1(1+exp(-x)). f(x)=1/1(1+exp(−x)).
有了dropout，前馈操作就变成了(图3b)
这里*代表element-wise product。对任意层 l l l ， r ( l ) r^{(l)} r(l) 是独立Bernoulli分布的随机变量的向量，每个随机变量为1的概率是p。
该向量被采样并与该层的输出 y ( l ) y^{(l)} y(l)相乘，以创建thinned outputs y ~ ( l ) \widetilde{y}^{(l)} y (l)。稀释后的输出被用作下一层的输入。这个过程应用于每一层。这相当于从一个更大的网络中抽样一个子网络。为了学习，损失函数的导数通过子网络反向传播。如图2所示，在测试时，权重按比例缩放 W t e s t ( l ) = p W ( l ) W^{(l)}_{test}=pW^{(l)} Wtest(l)=pW(l)。得到的神经网络没有使用dropout。
5. Learning Dropout Nets
5.1 Backpropagation
dropout神经网络可以用类似于标准神经网络的随机梯度下降来训练。唯一的区别是，对于一个小批量的每个训练样本，我们都通过dropping out单元来抽样一个精简的网络。该训练样本的前向和后向传播仅在该细化网络上完成。许多方法被用来改善随机梯度下降，如动量、退火学习率和L2权值衰减。这些被发现对dropout神经网络也很有用。
发现有一种特殊的正则化形式对dropout约束特别有用，在每个隐藏单元处传入的权重向量的范数的上界被固定为常数c。换句话说，如果w表示任何隐藏单元上的权向量，则在约束条件
∥ w ∥ 2 ≤ c \parallel w\parallel_2\le c ∥w∥2≤c 下对神经网络进行优化。这个约束是在优化过程中通过将w投影到一个半径为c的球的表面。这也被称为最大范数正则化，因为它意味着任何权重的范数可以取的最大值是c。常数c是一个可调超参数，它是使用验证集确定的。最大范数正则化以前曾用于协同过滤（Srebro和Shraibman，2005）。即使在不使用dropout的情况下，它也能显著地提高深神经网络的随机梯度下降训练性能。
尽管dropout本身带来了显著的改善，但与最大范数正则化、大衰减学习率和高动量比一起使用比单独使用dropout提供了更显著的推动。一个可能的理由是，将权重向量限制在一个固定半径的球内，使得使用一个巨大的学习率成为可能，而不会出现权重爆炸的情况。然后，dropout提供的噪声允许优化过程探索权重空间中原本很难到达的不同区域。随着学习率的下降，优化的步骤越来越短，因此所做的探索也越来越少，并最终达到最小值。
6.5 Comparison with Standard Regularizers
为了防止神经网络的过度拟合，提出了几种正则化方法。其中包括L2权重衰减（更普遍的是Tikhonov正则化（Tikhonov，1943））、lasso（Tibshirani，1996）、KL稀疏性和最大范数正则化。dropout可以看作是神经网络正规化的另一种方式。在本节中，我们将使用MNIST数据集将dropout与这些正则化方法中的一些进行比较。
用随机梯度下降法训练具有ReLUs的同一网络结构（784-1024-1024-2048-10）。结果如表9所示。利用验证集得到了与各种正则化相关的不同超参数（衰减常数、目标稀疏性、退出率、最大范数上界）的值。我们发现，与最大范数正则化相结合的dropout给出了最小的泛化误差。
7. Salient Features
7.1 Effect on Features
在一个标准的神经网络中，每一个参数所接收到的导数告诉它应该如何变化，以便在所有其他单元都在做的情况下减少最终损失函数。因此，单元的变化可能会修正其他单元的错误。这可能导致复杂的协同适应。 这反过来又会导致过度拟合，因为这些共同适应并没有泛化到看不见的数据。我们假设，对于每个隐藏单元，dropout通过使其他隐藏单元的存在不可靠来防止协同适应，因此，隐藏单元不能依赖其他特定单元来纠正错误。它必须在其他隐藏单元提供的各种不同上下文中表现良好。为了直接观察这一效果，我们研究了一级特征，这些特征是由在有或没有dropout的视觉任务上训练的神经网络学习的。
图7a显示了由MNIST上的自动编码器学习到的特性，该编码器具有256个校正线性单元的单个隐藏层，且没有丢失。图7b显示了由相同的自动编码器学习的特性，该编码器使用p=0.5的隐藏层中的dropout。
两个自动编码器都有相似的测试重建错误。然而，很明显，图7a中所示的特征已经共同适应以产生良好的重构。每一个隐藏的单元本身似乎并没有检测到有意义的特征。另一方面，在图7b中，隐藏单元似乎在图像的不同部分检测边缘、笔划和斑点。这表明辍学确实会破坏共适应，这可能是它导致较低的泛化误差的主要原因。
7.2 Effect on Sparsity
**我们发现作为dropout的副作用，隐藏单元的激活变得稀疏，即使不存在诱导稀疏的正则化。因此，dropout自动导致稀疏表示。**为了观察这一效果，我们选取在前一节中训练过的自动编码器，观察从测试集中随机抽取的小批量上隐藏单元激活的稀疏性。
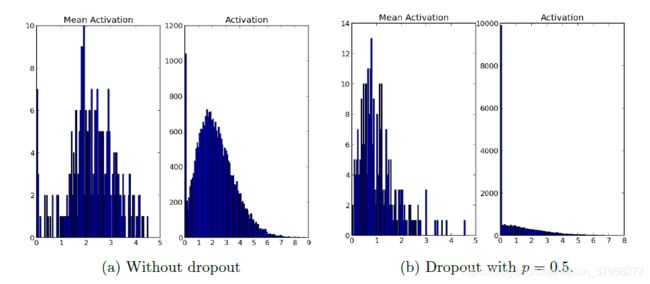
图8：dropout对稀疏性的影响。两个模型都使用了ReLUs。左：平均激活直方图显示，大多数单位的平均激活率约为2.0。激活的柱状图显示了一个远离零的巨大模式。很明显，有很大一部分单元具有高活性。右图：平均激活率直方图显示，大多数单位的平均激活率较小，约为0.7。激活的直方图显示在0处有一个尖锐的峰值。很少有单位有高激活率。
我们发现作为dropout的副作用，隐藏单元的激活变得稀疏，即使不存在诱导稀疏的正则化。因此，dropout自动导致稀疏表示。为了观察这一效果，我们选取在前一节中训练过的自动编码器，观察从测试集中随机抽取的小批量上隐藏单元激活的稀疏性。图8a和图8b比较了两种模型的稀疏性。在一个好的稀疏模型中，对于任何数据情况，应该只有几个高度激活的单元。此外，数据案例中任何单元的平均激活率都应该很低。为了评估这两个特性，我们为每个模型绘制了两个直方图。对于每个模型，左边的直方图显示了整个小批量中隐藏单元的平均激活率分布。右边的直方图显示了隐藏单元激活的分布。
通过比较激活的直方图，我们可以看到，与图8a相比，图8b中具有高激活的隐藏单元更少，这可以从不使用dropout的网络远离零的显著质量中看出。dropout网络的平均激活率也较小。对于自动编码器而言，在没有dropout时，隐藏单元的总体平均激活率接近2.0，但使用dropout时，则降至0.7左右。
7.4 Effect of Data Set Size
对一个好的正则化器的一个测试是，它应该使在小数据集上训练大量参数的模型能够获得好的泛化误差。本节探讨在前馈网络中使用dropout时更改数据集大小的效果。用标准方法训练的大型神经网络在小数据集上过拟合。为了看dropout是否有帮助，我们在MNIST上进行分类实验，并改变网络的数据量。
这些实验的结果如图10所示。从MNIST训练集中随机选择100、500、1K、5K、10K和50K大小的数据集。所有数据集使用相同的网络体系结构（784-1024-1024-2048-10）。在所有隐藏层执行p=0.5的dropout，在输入层执行p=0.8的dropout。可以观察到，对于非常小的数据集（100500），该模型并没有任何改进，它有足够的参数可以对训练数据进行过度拟合，即使所有的噪声都来自于dropout。随着数据集大小的增加，从dropout中获得的收益增加到一个点，然后下降。这表明，对于任何给定的体系结构和dropout率，都有一个“最佳点”，对应于一些数据量，尽管存在噪音，但这些数据量足够大，无法记忆，但不会太大，因此无论如何，过度拟合都不是问题。
预计dropping单元将降低神经网络的容量。如果n是任何层中隐藏单元的数目，p是保留一个单元的概率，那么在期望的情况下，在dropout后，将只出现pn个单元，而不是n个隐藏单元，而且这组pn单元每次都不同，并且不允许单元自由地建立协适应（build co-adaptations freely）。因此，如果一个n大小的层对于一个标准的神经网络在任何给定的任务上都是最优的，那么一个好的退出网络应该至少有n/p单位。我们发现这对于在卷积网络和全连接网络中设置隐藏单元的数量是一个有用的启发。
A.2 Learning Rate and Momentum
与标准随机梯度下降相比，dropout在梯度中引入了大量噪声。因此，许多梯度往往相互抵消。为了弥补这一点，dropout网络通常应该使用标准神经网络最佳学习率的10-100倍。另一种降低噪声影响的方法是使用高动量。虽然动量值为0.9对于标准网络来说是很常见的，但是我们发现0.95到0.99之间的值工作得更好。使用高学习率和/或动力显著加快学习速度。
A.3 Max-norm Regularization
虽然大动量和学习速率加快了学习速度，但它们有时会导致网络权值变得非常大。为了防止这种情况，我们可以使用最大范数正则化，这将每个隐藏单元的传入权重向量的范数约束为常数c。c的典型值范围为3到4。
A.4 Dropout Rate
ularization
虽然大动量和学习速率加快了学习速度，但它们有时会导致网络权值变得非常大。为了防止这种情况，我们可以使用最大范数正则化，这将每个隐藏单元的传入权重向量的范数约束为常数c。c的典型值范围为3到4。
A.4 Dropout Rate
dropout引入了一个额外的超参数，即保持单位p的概率。这个超参数控制dropout的强度。p=1，表示无dropout，p值低表示dropout较多。隐藏单元的典型p值在0.5到0.8之间。对于输入层，选择取决于输入类型。对于实值输入（图像块或语音帧），典型值为0.8。对于隐藏层，p的选择与隐藏单元数n的选择相结合。较小的p需要较大的n，这会减慢训练速度并导致欠拟合。大p可能不会产生足够的dropout以防止过拟合。