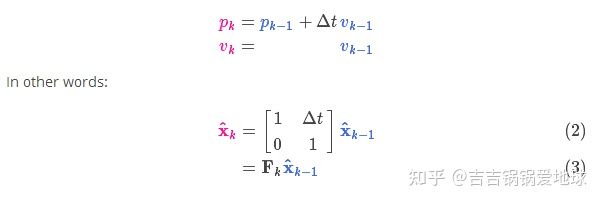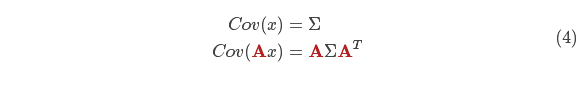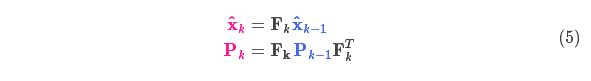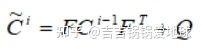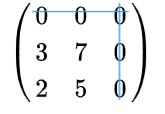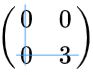DeepSORT 多实时目标跟踪，pytorch代码，解析

原文：DeepSORT 多实时目标跟踪，pytorch代码，解析 - 知乎

​

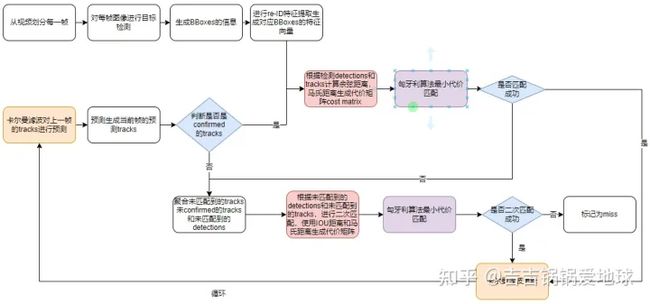
整个目标跟踪大体上是这个流程图：

1.目标检测

陈述的是图里的这一部分：

由于目标跟踪的目标检测模块的通用性，关于目标检测我就不做介绍了，可以换成诸如：YOLOV4，YOLOV3,YOLOV5,Faster RCNN,Fast RCNN等目标检测器。

这里以YOLOV4或V3的输出为例，总之根据目标检测的输出是三个张量。假设他们的shape分别为[batch_size,256,13,13],[batch_size,256,26,26],[batch_size,256,52,52]。经过了复杂的后处理后，他们的输出shape变为[n,7]。

这里的n表示可能的Bounding Boxes的数量，7表示：4个坐标（x1，y1，x2，y2），2个置信度（0-1之间），1个类别ID。

    def run(self):
        idx_frame = 0   #表示第几帧
        while self.video.grab():  #从视频里面抓取下一帧
            idx_frame += 1
            if idx_frame % cfg.frame_interval:#如果不为0,如果frame_interval=1，表示每帧都用来推理，为2表示每隔一帧进行推理，依次类推
                continue

            start = time.time()#计时
            #===============单个视频帧处理=================
            _, ori_im = self.video.retrieve() #返回解码后的视频帧
            boxes = self.detectOneImage.detect_one_image(ori_im)#boxes是对应的object的bbox的坐标，当前图片帧里有多少个目标=len(boxes)

这里的代码中，从视频里解析每个图片帧，然后放到目标检测器里进行检测（代码的self.detectOneImage.detecti_one_image(ori_im)。返回检测到的shape=[n,7]。这个目标检测器包含了复杂的前处理和后处理部分，被封装成一个对象了。

            if len(boxes)==0:
                continue
            boxes = torch.tensor(boxes)
            bbox_xywh = boxes[:, :4] #bbox坐标,格式为center_x,center_y,box_w,box_h
            cls_conf = boxes[:,5]*boxes[:,4]  #类别的置信度
            class_ids = boxes[:,6] #类别id

然后下面进行为空判断，并取出对应的数据。

2.目标跟踪

            bbox_xywh[:, 3:] *= 1.2  # 将bbox扩大一点点，以防止bbox太小
            # cls_conf = cls_conf[mask]
            #===================进行跟踪=========================
            outputs = self.deepsort.update(bbox_xywh, cls_conf, ori_im,class_ids)
            #=================绘画bbox，可视化=====================
            if len(outputs) > 0:
                bbox_xyxy = outputs[:, :4]
                identities = outputs[:,-2]
                classes_str = [self.classes[id] for id in outputs[:, -1]]
                ori_im = draw_boxes(ori_im,bbox_xyxy,identities,classes_str)

            end = time.time()
            print("One Image spend time: {:.03f}s, fps: {:.03f}".format(end - start, 1 / (end - start)))

            if cfg.display:
                cv2.imshow("test", ori_im)
                cv2.waitKey(1)

            if cfg.save_path and os.path.isdir(cfg.save_path):
                self.writer.write(ori_im)

首先将目标检测的框扩大，原因是因为目标检测一般定位已经相对准确了，过于严格的定位，会导致跟踪困难，并且若定位有误差，会加大跟踪的难度。然后通过封装的跟踪器，进行跟踪。返回跟踪后的Bounding Boxes，然后进行可视化，展示可视化，保存视频。

下面将会详细讲解

outputs = self.deepsort.update(bbox_xywh, cls_conf, ori_im,class_ids)

里发生的过程。

    def update(self, bbox_xywh, confidences, ori_img,class_ids):
        '''
        bbox_xywh:bounding box的中心坐标和w,h。
        confidence:置信度
        ori_img:用cv2打开的原始图片，为BGR格式
        '''
        ori_img = cv2.cvtColor(ori_img, cv2.COLOR_BGR2RGB)    #默认的cv2图像是BGR，所以转换成RGB
        self.height, self.width = ori_img.shape[:2]
        #生成检测
        features = self._get_features(bbox_xywh, ori_img)#将ori_img对应用box切片后进行特征提取，是一个向量

首先介绍一下这三个参数的意义。

bbox_xywh:是经过目标检测到的Bounding Boxes的中心坐标xy和宽高wh。

confidences：是对应Bounding Boxes的置信度，表示该Bounding Boxes里是预测的那个物体的概率。

ori_img：是Opencv打开的原始图片。

代码，然后经过色域转换BGR->RGB格式，放入ReID网络。

3.ReID网络

陈述的是图的这一部分：

ReID网络是DeepSORT的主要创新点。通过外观信息，来获取待跟踪的Bounding Boxes的抽象特征，并计算与上一帧的匹配结果Bounding Boxes的余弦距离，和马氏距离，构建代价矩阵。

ReID网络，全称行人ID重识别（Pedestrian Re-identification，ReID），广泛应用在安防，视频监控领域。为同一个人，但是在不同地点，不同姿态下，分配唯一ID的行为。图源：小白入门系列——ReID(一)：什么是ReID？如何做ReID？ReID数据集？ReID评测指标？ - 知乎

可以理解为主要为了防止跟踪器在跟踪的时候导致大量的目标ID切换问题。可以认为ReID是一种特征提取网络。整个模型的网络结构如下，可以看成是一个层数比较少的特征提取网络。（手工绘图，转载以及使用注明图片来源）

在目标跟踪的流程是，对检测到的每个Bounding Boxes的位置，去原始的图片中，截取对应的目标方框图，然后放入到Re-ID网络中，由于已经加载好了预先训练好的权重，所有，放入这个Re-ID网络后，进行前向推理后，经过embedding后，获得对应的每个Bounding Boxes的特征向量，也就是对应着每个Bounding Boxes的外观信息。

3.1使用Detection类封装经过Re-ID网络后的特征

        bbox_tlwh = self._xywh_to_tlwh(bbox_xywh)#转换bbox的格式
        #下面这个confidences={Tensor:(2,4)}，第0维表示检测到几个box，并且这个置信度要大于设定的阈值
        '''detections保存了所有的box的信息，每个Detection对象包含了满足阈值的目标置信度，box的特征向量，tlwh的box坐标'''
        detections = [Detection(bbox_tlwh[i], conf, features[i]) for i, conf in enumerate(confidences) if
                      conf > cfg.min_confidence]

        #应用非极大值抑制
        boxes = np.array([d.tlwh for d in detections])#格式为tlwh的所有目标的box坐标信息
        scores = np.array([d.confidence for d in detections])#格式为单个float数的所有box的目标置信度信息
        indices = non_max_suppression(boxes, cfg.nms_max_overlap, scores)  #返回经过NMS剩下boxes的索引
        detections = [detections[i] for i in indices]   #只选取nms过后的索引的detections

接下来的步骤，主要使用一个名为Detection的类，将对应的特征向量集合和置信度集合，以及坐标，封装成Detection的数组，命名为detectioons。并再一次应用非极大值抑制算法。过滤一些detection。非极大值抑制的函数。

indices = non_max_suppression(boxes,cfg.nms_max_ouverlap,scores)#进行nms算法

非极大值抑制(No-maximum supprision,NMS)，参考另一篇博文：

吉吉锅锅爱地球：NMS详解（代码）非极大值抑制（Non Maximum Suppression）1 赞同 · 0 评论文章正在上传…重新上传取消

4.基于卡尔曼滤波的先验状态估计用于跟踪预测

陈述的是这一部分：

下面将详细讲解卡尔曼滤波的意义。

4.1什么是卡尔曼滤波

卡尔曼滤波(Kalman Filter)是一个优化自回归数据的处理算法，是现代控制理论的一种经典算法，能够在系统存在许多不确定的情况下，通过之前的信息，来估计系统的状态。广泛应用在关于时间序列的分析领域中。

先给出卡尔曼滤波的通用表达式。

卡尔曼滤波的预测式的通用表达式为：

卡尔曼滤波预测的一般通用表达式

其中， xt 表示系统在 t 时刻系统状态的均值向量， Ak 表示k时刻的状态转移矩阵， Pk 表示k时刻的协方差矩阵， Qk,Bku→k 表示系统在k时刻的噪声矩阵。带 ~ 表示预测的估计矢量。

卡尔曼滤波的更新式的通用表达式为：

卡尔曼滤波更新的一般通用表达式

其中, z→k 表示k时刻所测量到的均值向量， K 表示卡尔曼增益， H 表示从预测空间转换到检测空间的转移矩阵。

简单来说：系统估计/预测出一个结果，现实测量出一个结果。这俩都不对，两个数据根据稳定性加权，得到一个数值，认为这个加权算出来的这个最对。

案例：对一条直线上行驶的一个小车（看作质点）的状态进行估计，假设无外力作用，即保持初速度持续不断的运动。假设马尔科夫性，即当前时刻状态x(t)只与上一时刻小车的状态x(t−1)有关，给出一个递推方程x(t)=Ax(t−1)。理论上可以通过这个方程求出任意时刻的状态，但是事实上会受到不确定因素的影响。

我们假设每个状态分量受到的不确定因素（噪声）的整体服从正态分布，那么在t0时刻，小车的状态分量也就服从正态分布，现在对小车进行状态估计。

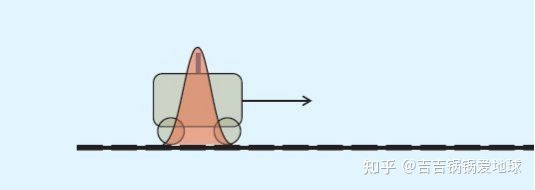
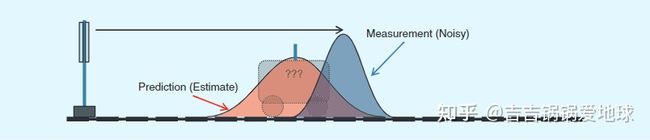
小车是一个质点，他的状态（位置，速度等）的初始值也是一个不确定的值，符合一个高斯分布，如图所示。

我们的目的是要通过状态转移矩阵A来估计小车在t1时刻的状态。

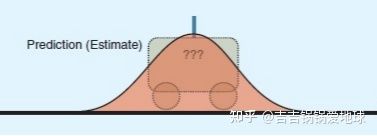
可以看到小车的状态分布变宽了，因为不确定因素增加了。

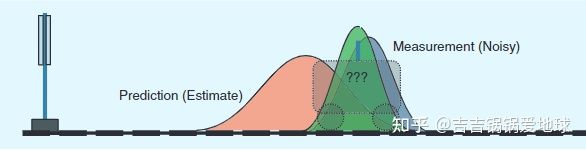
状态转移矩阵是指小车从t0的状态变到t1状态的转移过程矩阵。这时为了避免不确定度带来的过大的偏差，我们在t1时刻测量一次小车的位置和速度信息，如下图深色分布：

由于测试的小车的位置和速度也是一个大概的值（估计值 ），也包含了一定的误差，所以也是一个符合高斯分布的。

由于测量值也是一个大概的值，不是完完全全的精确值，由于车辆遇到沟壑，以及速度的突变不符合状态转移矩阵，导致测量值也不太准。这个时候到底是选取哪一个值呢？是橙色的估计值，还是蓝灰色的测量值呢？这就涉及到卡尔曼滤波的卡尔曼增益 K 。用来衡量两者的权重。

绿色区域是估计值和测量值融合后的结果。两者相交的部分的横坐标就是卡尔曼增益

此外，由于小车状态的各个变量之间，不是独立的，比如小车的速度和当前位置就是具有一定关系的：速度大，在相同时间内，位置就变化大，速度小，在相同时间内，位置变化就小。而协方差恰好来表示多个变量之间的相关性简而言之，矩阵中的每个元素 Σij 表示第 i 个和第 j 个状态变量之间的相关度。可以很明显的发现，协方差是一个对称矩阵，交换协方差的i和j，协方差是不变的。

因此，在每个时刻我们都需要估计小车的两个值，均值向量和协方差矩阵。

我们首先引入一个物理中的运动学公式来表达小车的状态变化过程。

这里的P是位置，V是速度，可以看出是一个匀速运动模型。

小车是匀速运动的，所以有速度 Vk=Vk−1 。整理后可以表达为（3）式。和卡尔曼滤波的预测式相同（这里暂时不考虑噪声 Bku→k 。）

那么协方差矩阵呢？尝试在协方差 Pk−1 的每个元素上×一个矩阵A，那么这个协方差就会变成：

注：协方差回顾： https://blog.csdn.net/hustqb/article/details/90264432

结合（3）式和（4）式，得：

如果系统包含了外部控制，比如小车并不是匀速运动的，内部可以加油门。因此，假设小车符合匀加速直线运动，则运动学公式为：

用矩阵形式表达为：

这是存在可控的内部作用情况下的情形，如果有存在不可控的外部变量。即未知变量的干扰，那么上述（6）式和（5）式子，可以表达为下式：

这就是卡尔曼滤波的预测式。

注意：
卡尔曼滤波利用了两个高斯分布相乘，相加依旧是高斯分布这一特性。
卡尔曼滤波其实是贝叶斯后验估计的另一表达形式

4.2DeepSORT中的卡尔曼滤波预测式

在卡尔曼滤波的一般表达式中，忽略均值向量的后面部分（因为是匀速模型）。所以上面的卡尔曼滤波的预测表达式变为：

x~=Akxk−1P~=AkPk−1AkT+Q

将这个卡尔曼滤波的预测的通用表达式应用到目标跟踪（目标跟踪的卡尔曼滤波是匀速卡尔曼滤波模型）中，用如下式子表达。

也可以展开为：

可以看到这是一个匀速运动的卡尔曼滤波模型。

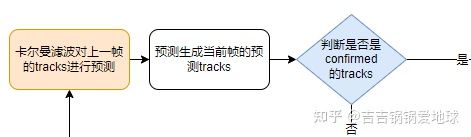
在代码里的具体体现如下，这个函数是用来对上一帧的跟踪Track进行预测，预测出当前的跟踪Track。

代码片段

#这句代码位于DeepSORT类对象里        
self.tracker.predict()#track预测

这个函数里面的内容如下:

#这是跟踪Tracker类对象的方法   
 def predict(self):
        """
        向前传播跟踪状态分布
        这个函数应该每个step都被调用一次，在update()之前
        """
        #对每一条track使用卡尔曼滤波的predict
        for track in self.tracks:
            track.predict(self.kf)

其中，对每个track，执行一次卡尔曼滤波预测。对应track.predict(self.kf)里面的代码如下：

#这是Track跟踪的代码，Track通常翻译成跟踪，或者轨迹    
def predict(self, kf):
        """
        使用卡尔曼滤波器预测step，将状态分布传播到当前step。
        使用卡尔曼滤波的predict方法对每条track进行状态（8x8矩阵的均值和协方差）预测，
        基于上一时刻的状态对当前时刻的状态和不确定性进行预测。（根据线性运动学方程进行预测

        mean(u,v,y,h,x1,y1,y~,h~),x=vt,预测不确定性covariance）
        Parameters
        ----------
        kf : kalman_filter.KalmanFilter
            卡尔曼滤波器

        """
        #根据上一时刻的track状态预测出来当前时刻的均值和协方差计算
        self.mean, self.covariance = kf.predict(self.mean, self.covariance)
        #这个track每次predict时就将age+1,年龄越大的tracks越晚被跟踪。
        self.age += 1
        self.time_since_update += 1

卡尔曼滤波，主要是根据上一时刻的track状态（均值和协方差）预测出当前时刻的均值和协方差。

其中kf.predict()内容如下，这是卡尔曼滤波预测式的主要部分。

    def predict(self, mean, covariance):
        """
        运行卡尔曼滤波预测步骤，计算（8x8的矩阵和协方差）

        Parameters
        ----------
        mean : ndarray:(8,)
            上一时刻的track的后验估计均值，一个8维均值向量
        covariance : ndarray:(8x8)
            上一时刻的track的后验估计协方差，8x8的协方差矩阵

        Returns
        -------
        (ndarray, ndarray)
            返回预测状态的均值向量和协方差矩阵。 未观察到的速度被初始化为 0 均值。
        """
        std_pos = [ #位置
            self._std_weight_position * mean[3],
            self._std_weight_position * mean[3],
            1e-2,
            self._std_weight_position * mean[3]]
        std_vel = [ #速度
            self._std_weight_velocity * mean[3],
            self._std_weight_velocity * mean[3],
            1e-5,
            self._std_weight_velocity * mean[3]]
        #初始化噪声矩阵Q
        motion_cov = np.diag(np.square(np.r_[std_pos, std_vel]))
        #均值更新式和协方差更新式,M' = FM
        mean = np.dot(self._motion_mat, mean)
        #C'=FCF^T+Q
        covariance = np.linalg.multi_dot((
            self._motion_mat, covariance, self._motion_mat.T)) + motion_cov

        return mean, covariance

关于跟踪tracks的Track对象，是一个Track类，每个Track的初始化函数如下。关于参数的介绍也在里面。

class Track:
    """
    一个目标跟踪track，状态空间向量为(x,y,a,h)，关联着它们的速度信息

    Parameters
    ----------
    n_init : int
        track被confirmed前的连续detections的数量，如果在开始的n_init帧内发生miss，
        则track的状态就会被设置为Deleted
    max_age : int
        track状态被设置为Deleted之前的最大连续miss次数。
    mean : ndarray
        初始状态分布的均值向量
    covariance : ndarray
        初始状态分布的协方差矩阵
    track_id : int
        track分配的唯一ID
    hits : int
        测量更新的总数
    age : int
        第一次发生以来的总帧数
    time_since_update : int
        自上次测量更新以来的总帧数。
    state : TrackState
        目前的track状态.
    features : List[ndarray]
        特征缓存。 在每次测量更新时，相关的特征向量都会添加到此列表中。
    """
    def __init__(self, mean, covariance, track_id, n_init, max_age,class_id,
                 feature=None):
        self.mean = mean    #均值
        self.covariance = covariance    #协方差
        self.track_id = track_id    #track的id
        self.class_id = class_id
        #===========初始化类别字典================
        self.classes = {}

        #hits代表匹配了多少次，成功连续匹配次数达到_n_init=3时才会将将状态设置为confirmed
        self.hits = 1
        self.age = 1    #age越大则越晚被跟踪，每次调用卡尔曼滤波预测时候就会+1

        #每次调用卡尔曼滤波预测时候就会+1,每次调动update的时候就会重置为0，意思就是每次成功匹配时，重置为0,否则+1
        self.time_since_update = 0

        self.state = TrackState.Tentative
        #每个track对应多个features，每次update都将最新的features添加到列表里
        self.features = []
        if feature is not None:
            self.features.append(feature)

        self._n_init = n_init
        self._max_age = max_age #最大存活期限

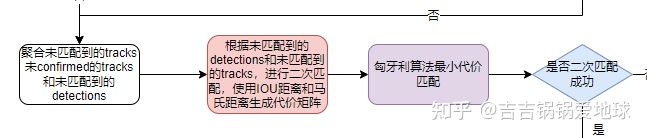
5.基于外观信息和IOU的级联匹配

陈述的是这一部分：

由于基于外观信息和IOU的匹配都用到了匈牙利算法求解最小代价分配问题，因此，首先简单介绍一下匈牙利算法。

5.1基于匈牙利算法求解最小代价分配问题

是库恩(W.W.Kuhn)在1955年构造的一个关于在多项式时间里，求解两个结合的二分图分配问题的一种算法。利用了匈牙利数学家康尼格(D.Konig)的定理求解了这个问题：

通常用于求解最小代价分配问题。直接说人话，案例讲解：

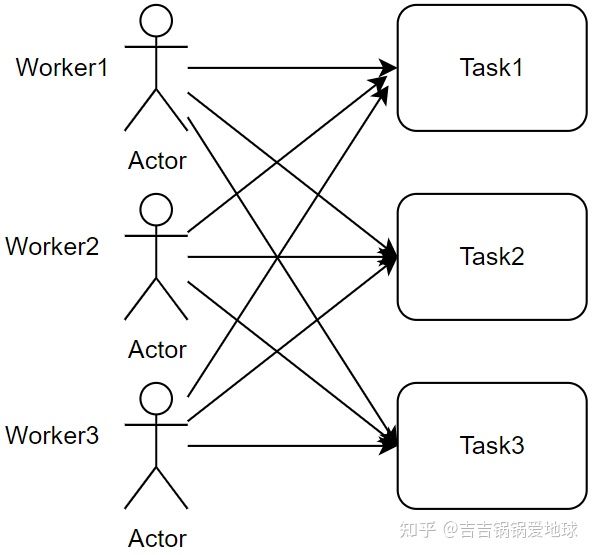
假设有如下一个实际问题。这里有n份工作任务，有n个工人，每个工人完成工作所需的成本不同（可以时间成本，可以是经济成本），但是由于每个工人在同一时间只能做一个工作，每个工作因此只能分配给一个工人，需要给出一个算法，求出总的花费成本最低。

绿色的线表示整体最小代价分配的方案。用一个表格，或者说矩阵表示为：

	Task1	Task2	Task2
Worker1	10	15	19
Worker2	9	18	5
Worker3	6	14	3

那么上面这个表格或者说是矩阵，的第(i,j)个元素的值就对应着第i个工人分配给他第j个任务的成本。因此上面这个矩阵也就称为代价矩阵。

D. F. Crouse, "On implementing 2D rectangular assignment algorithms," in IEEE Transactions on Aerospace and Electronic Systems, vol. 52, no. 4, pp. 1679-1696, August 2016, doi: 10.1109/TAES.2016.140952.

算法流程如下：

0.创建一个称为代价矩阵cost matrix的nxm矩阵，如果m!=n那么进行矩阵填充（填充原矩阵的最大元素即可）。让行数=列数。并令k=min(n,m)。比如：

这里的k=3.

(1015991856143)

1.对于这个矩阵的每一行，找到最小的元素，然后从这一行的每个元素减去这个最小的元素。

(16041303110)

2.对于这个矩阵的每一列，找到最小的元素，然后从这一列的每个元素减去这个最小的元素。

(000370250)

3.对于这个矩阵，用数量最小的直线覆盖所有的0元素，如果线段数量=K那么，就找到了这样的最优分配。

否则，找到没有被直线覆盖的元素中的最小的一个值，让每个没有完全被直线覆盖的元素行中的元素-这个值，让每个完全被直线覆盖了的列的元素+这个值。然后重复执行步骤3。

两条直线覆盖了所有0元素，然后用每个没有被直线完全覆盖的行减去最小元素2

然后让每个完全被直线覆盖的列加上最小元素2，然后添加新的直线

现在直线数量=3了，所以停止。

4.找到最优分配的过程可以表述为。依次找到只有一个0的元素，取出行和列。

取出了第2行3列的元素，并重新构建矩阵

第二次选出第3行，第1列的元素。

所以，上述的代价矩阵的最优分配矩阵为：

	Task1	Task2	Task3
Worker1		15
Worker2			5
Worker3	6

这就是匈牙利算法的解释。当然，我们只需要了解这个算法是干嘛的就行。

在目标跟踪中，当前帧的检测器会生成Bounding Boxes的坐标位置和类别信息，而上一帧的跟踪器会进行预测生成Bounding Boxes的坐标和位置信息。两者如何一一配对呢？这就用到了之前的匈牙利匹配算法。

比如生成了一个有关于检测器Detections和跟踪器Tracks的代价矩阵。

	Track1	Track2	Track3	Track4
Detection1	21	10	0	90
Detection2	56	62	11	90
Detection3	20	77	90	90
Detection4	10	80	20	90

其中这里面的元素都是通过距离计算处理出来的，具体有余弦距离，欧氏距离和IOU距离，前两个用于第一次匹配，IOU距离用于第二次匹配。

        def gated_metric(tracks, dets, track_indices, detection_indices):
            '''
            根据外观信息和马氏距离，计算卡尔曼滤波预测到的tracks和当前时刻检测到的
            detections的代价矩阵
            '''
            features = np.array([dets[i].feature for i in detection_indices])
            targets = np.array([tracks[i].track_id for i in track_indices])
            #基于外观信息，计算tracks和detections的余弦距离代价矩阵
            cost_matrix = self.metric.distance(features, targets)
            #基于马氏距离，过滤掉代价矩阵中的一些不合理的项，将其设置为一个较大的值
            cost_matrix = linear_assignment.gate_cost_matrix(
                self.kf, cost_matrix, tracks, dets, track_indices,
                detection_indices)
            return cost_matrix

上述代码用来根据指定的方式（余弦距离，欧式距离，IOU距离），计算用于匈牙利算法的代价矩阵，然后利用马马氏距离修正。其中的features是经过re-ID后的Bounding Boxes的特征向量，包含了类别信息。track_id是对应根据上一帧预测到当前帧的跟踪Tracks。

5.2距离度量——欧几里得距离，余弦距离，马氏距离，IOU距离介绍

1.余弦距离

余弦距离实际上是指两个向量之间的距离，严格意义上来说，余弦距离是指的两个向量在空间中的相似度。

Nguyen H V, Bai L. Cosine similarity metric learning for face verification[C]//Asian conference on computer vision. Springer, Berlin, Heidelberg, 2010: 709-720.

Hieu V. Nguyen 和Li Bai 在使用了余弦相似度来进行人脸的特征向量的匹配。因此使用余弦距离对tracks和detections的结果进行度量，是一种合理且常用的方法。余弦距离只关注两个向量的方向的差异性，而对向量的长度不敏感。余弦相似度的范围为[-1,1]，当两个向量完全相似的时候，其余弦相似度为1。而余弦距离表示为1-余弦相似度。

2.欧式距离，欧几里得距离(Euclidean距离）

3.Mahalanobis距离，马氏距离，马哈拉诺比斯距离

马氏距离由印度统计学家P. C. Mahalanobis提出，是修正的欧几里得距离，所以，通常情况下，可以看作是欧氏距离的一种修正方案，是一种有效的计算两个位置样本集合的相似度的方法，欧式距离不考虑在多维空间下维度之间的关系，而马氏距离则考虑到了各个特性之间的联系。并且独立于尺度的，也就是说马氏距离与度量尺度无关。

De Maesschalck R, Jouan-Rimbaud D, Massart D L. The mahalanobis distance[J]. Chemometrics and intelligent laboratory systems, 2000, 50(1): 1-18.

可以看出，马氏距离和欧式距离很接近，诚然，当协方差矩阵为一单位矩阵的时候，马氏距离退化为欧氏距离，马氏距离有如下优点：

1）马氏距离不受量纲的影响，两个样本之间的距离与量纲无关，与测量出的样本单位无关，与数据是否已经被标准化或中心化是无关的。

2）马氏距离，考虑了样本之间的关联关系，排除了多个变量之间的相关性对结果的干扰。

在目标跟踪中，使用马氏距离的同时考虑了外观和运动的信息。这种匹配的方式考虑了状态的不确定的程度。通常利用自由度为4的卡方分布的分位值作为其阈值，用来排除不可能的关联。

马氏距离的代码解析可以见链接，余弦距离和欧式距离比较简单就不贴了。

吉吉锅锅爱地球：DeepSORT中的马氏距离(马哈拉诺比斯距离Mahalanobis Distance) 代码讲解13 赞同 · 4 评论文章正在上传…重新上传取消

4.IOU距离

从IOU距离的名字就可以看出(Intersection Over Union，交并比)。通过这个名字我们可以大体上看得出IOU的意思。也就是两个Bounding Boxes的交集/并集的面积。而IOU距离则表示为：1-IOU距离

如图所示，带表两个Boundinx Boxes的面积交集 比 两个Bounding Boxes的面积并集。衡量的是两个Bounding Boxes的重合程度。（值越大，重合度越高，值越低重合度越低）

所以对应的IOU距离则表示，两个Bounding Boxes相距越近，IOU距离越小，两个Bounding Boxes相距越远，IOU距离越大。

def iou(bbox, candidates):
    """
    计算一个bbox和candidates的交并比

    Parameters
    ----------
    bbox : ndarray
        一个bounding boxes，格式为(top left x, top left y, width, height).
    candidates : ndarray
        一个ndarray的矩阵，每行的坐标格式为(top left x, top left y, width, height).

    Returns
    -------
    ndarray
        在bbox和每个candidate的交集，位于[0,1]
        这个值较大的话意味着bbox的大部分都被candidate遮挡了

    """
    bbox_tl, bbox_br = bbox[:2], bbox[:2] + bbox[2:]    #获得左上点和右下点的坐标
    candidates_tl = candidates[:, :2]   #获得候选bbox的左上点
    candidates_br = candidates[:, :2] + candidates[:, 2:]   #获得候选bbox的右下点

    tl = np.c_[np.maximum(bbox_tl[0], candidates_tl[:, 0])[:, np.newaxis],  #获得两个bbox相交的左上点
               np.maximum(bbox_tl[1], candidates_tl[:, 1])[:, np.newaxis]]
    br = np.c_[np.minimum(bbox_br[0], candidates_br[:, 0])[:, np.newaxis],  #获得两个bbox相交的右下点
               np.minimum(bbox_br[1], candidates_br[:, 1])[:, np.newaxis]]
    wh = np.maximum(0., br - tl)    #右下-左上=bbox相交部分的长宽

    area_intersection = wh.prod(axis=1) #在axix=1处计算所有元素的乘积，因为所有的box和candidates都是多个，返回对应bbox相交面积
    area_bbox = bbox[2:].prod() #计算bbox的面积
    area_candidates = candidates[:, 2:].prod(axis=1)    #计算candidates的面积
    return area_intersection / (area_bbox + area_candidates - area_intersection)    #返回交并比

def iou_cost(tracks, detections, track_indices=None,
             detection_indices=None):
    if track_indices is None:   #判空处理
        track_indices = np.arange(len(tracks))
    if detection_indices is None:   #判空处理
        detection_indices = np.arange(len(detections))
    #先创建一个空的代价矩阵cost matrix
    cost_matrix = np.zeros((len(track_indices), len(detection_indices)))
    for row, track_idx in enumerate(track_indices): #逐个元素赋值
        if tracks[track_idx].time_since_update > 1: #只对time_since_update=0进行IOU赋值，其他的赋一个极大值
            cost_matrix[row, :] = linear_assignment.INFTY_COST
            continue

        bbox = tracks[track_idx].to_tlwh()  #bbox坐标转换从 tlah->tlwh
        candidates = np.asarray([detections[i].tlwh for i in detection_indices])    #从detections中获得candidates
        cost_matrix[row, :] = 1. - iou(bbox, candidates)    #计算IOU距离，并赋到代价矩阵里
        return cost_matrix

6.基于卡尔曼滤波后验状态估计用于检测更新

在4.1节中，展示了卡尔曼滤波的两个式子，分别是卡曼滤波的预测式，卡尔曼滤波的更新式。

其中卡尔曼滤波的更新式为：

其中, z→k 表示k时刻所测量到的均值向量， K 表示卡尔曼增益， H 表示从预测空间转换到检测空间的转移矩阵。

这一段代码中，计算并返回卡尔曼滤波更新式的 Hix~i 和 HiP~iHiT+R

    def project(self, mean, covariance):
        """
        将均值和协方差的状态分布矩阵/向量投影到测量/检测空间
        mean : ndarray 状态均值向量，8维数组
        covariance : ndarray 状态协方差矩阵(8x8维).
        """
        std = [
            self._std_weight_position * mean[3],
            self._std_weight_position * mean[3],
            1e-1,
            self._std_weight_position * mean[3]]
        # 初始化噪声矩阵R,4x4对角矩阵，对角线上值分别为中心点xy和ah的噪声
        innovation_cov = np.diag(np.square(std))
        # 将均值向量映射到detection空间，即Hx'
        mean = np.dot(self._update_mat, mean)
        #将协方差矩阵映射到检测空间，即HP'H^T
        covariance = np.linalg.multi_dot((
            self._update_mat, covariance, self._update_mat.T))
        #返回Hx',HP'H^+R,
        return mean, covariance + innovation_cov

下面是卡尔曼滤波的更新代码，这里使用了Cholesky分解来简化计算。

    def update(self, mean, covariance, measurement):
        """
        卡尔曼滤波更新步骤

        Parameters
        ----------
        mean : ndarray
            预测的状态均值向量 (8 dimensional).
        covariance : ndarray
            预测的状态协方差矩阵 (8x8 dimensional).
        measurement : ndarray
            4维度的测量向量(x, y, a, h)

        Returns
        -------
        (ndarray, ndarray)
            Returns the measurement-corrected state distribution.
        """
        #将mean和covariance映射到检测空间,获得Hx'和HP'H^+R
        projected_mean, projected_cov = self.project(mean, covariance)
        #cholesky分解
        chol_factor, lower = scipy.linalg.cho_factor(
            projected_cov, lower=True, check_finite=False)
        #卡尔曼增益计算K
        kalman_gain = scipy.linalg.cho_solve(
            (chol_factor, lower), np.dot(covariance, self._update_mat.T).T,
            check_finite=False).T
        #得到测量值的映射结果y=z-Hx'，z是检测结果
        innovation = measurement - projected_mean
        #均值更新式x = x'+Ky = x'+K(z-Hx')
        new_mean = mean + np.dot(innovation, kalman_gain.T)
        #协方差更新式P = (I-KH)P'，代码是P=P'-KSK^T
        new_covariance = covariance - np.linalg.multi_dot((
            kalman_gain, projected_cov, kalman_gain.T))
        return new_mean, new_covariance

因为内容较多，持续更新中，有不懂的或者个人理解有问题的，欢迎留言探讨