CV【3】：drop_out & drop_path

---

前言

本文主要对比了两种正则化方法：drop_out 和 drop_path

---

1. drop_out

1.1. 出现的原因

在机器学习的模型中，如果模型的参数太多，而训练样本又太少，训练出来的模型很容易产生过拟合的现象。在训练神经网络的时候经常会遇到过拟合的问题，过拟合具体表现在：模型在训练数据上损失函数较小，预测准确率较高；但是在测试数据上损失函数比较大，预测准确率较低。

过拟合是很多机器学习的通病。如果模型过拟合，那么得到的模型几乎不能用。为了解决过拟合问题，一般会采用模型集成的方法，即训练多个模型进行组合。此时，训练模型费时就成为一个很大的问题，不仅训练多个模型费时，测试多个模型也是很费时。

正则化可以有效地缓解上述两个问题

1.2. 概念

drop_out 是作为缓解卷积神经网络CNN过拟合而被提出的一种正则化方法，也叫做随机失活。

drop_out 可以作为训练深度神经网络的一种 trick 供选择。在每个训练批次中，通过忽略一半的特征检测器（让一半的隐层节点值为 0），可以明显地减少过拟合现象。这种方式可以减少特征检测器（隐层节点）间的相互作用，检测器相互作用是指某些检测器依赖其他检测器才能发挥作用。

简单来说就是在模型训练阶段的前向传播过程中，让某些神经元的激活值以一定的概率停止工作。

drop_out 确实能够有效缓解过拟合现象的发生，但是可能会减缓模型收敛的速度，因为每次迭代只有一部分参数更新，可能导致梯度下降变慢。

1.3. 工作原理

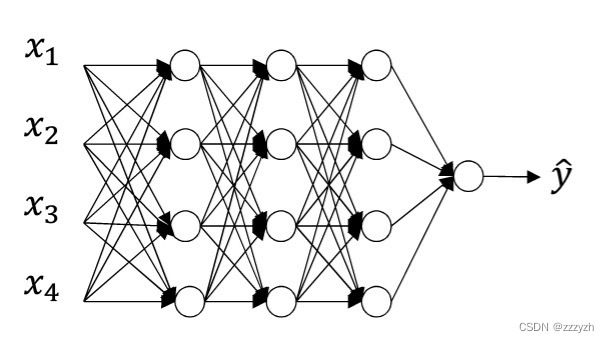
通过一个三层的简单神经网络来介绍 drop_out的工作原理，输入是 $X$，输出是 $Y$。正常的训练流程是首先把输入X通过网络进行前向传播，然后把误差反向传播以决定如何更新参数。

• 遍历神经网络的每一层节点，设置节点保留概率 keep_prob，即该层的节点有 keep_prob 的概率被保留，keep_prob 的取值范围在 0 到 1 之间，假设 keep_prob = 0.5
  • 通过设置神经网络该层节点的保留概率，使得神经网络不会去偏向于某一个节点（因为该节点有可能被删除），从而使得每一个节点的权重不会过大，来减轻神经网络的过拟合
• 删除神经网络的节点，并删除网络与移除节点之间的连接
  
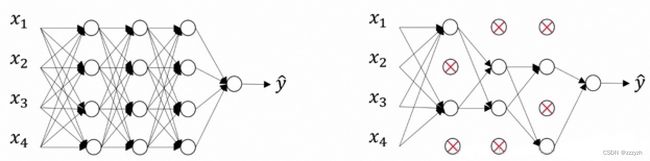
• 输入样本，使用简化后的网络进行训练
  • 让输入 $X$ 通过部分神经元失活的新网络（如上右图）进行前向传播，然后计算损失并把损失反向传播，一小批样本执行完这个过程后，根据梯度下降算法更新参数
• 不断重复这一过程：
  • 恢复失活的神经元
  • 重新让所有神经元以一定概率 p 失活（这次失活的和上次失活的神经元并不一定相同）
  • 让输入通过部分神经元失活的新网络进行前向传播，然后计算损失并把损失反向传播，新的一批样本执行完这个过程后，根据梯度下降算法更新参数

需要注意的是，drop_out 一般只在网络的训练阶段使用，而测试阶段不使用drop_out。这是因为如果在测试阶段使用 drop_out 可能会导致预测值产生随机变化（因为 drop_out 使节点随机失活）。而且，在训练阶段已经将权重参数除以 keep_prob 来保证输出的期望值不变，所以在测试阶段没必要再使用 drop_out

1.4. 尺度匹配问题

上面提到 drop_out 一般只在网络的训练阶段使用，而测试阶段不使用drop_out，也就是说训练时前向传播只使用没有失活的那部分神经元，而测试时使用的是全部的神经元，那么训练和测试阶段就会出现数据尺度不同的问题。

所以测试时，所有权重参数 $W$ 都要乘以 $1-p$，以保证训练和测试时尺度变化一致。

举例来说，假设输入是 100 个特征，没有使用 drop_out 之前，隐藏层第一层的第一个神经元的值可以表示为：

$$Z_1^1=\sum _{i=1}^{100}{w}_1^i{x}_1^i$$

不妨取 ${\omega }_1^i{x}_1^i=a$，那么此时 $Z_1^1=100a$

• 训练阶段使用 drop_out 时，若失活率 $p=0.3$，可以理解成只有 70 个神经元起作用，此时 $Z_1^1=\sum _{i=1}^{70}{\omega }_1^i{x}_1^i=70a$
• 而测试时没有 drop_out ，使用的是全部神经元，也就是 100a，不难发现使用 drop_out 后少了 30a，这就是训练阶段和测试阶段数据的尺度不一致

为了保证尺度的一致性，测试时所有权重参数 $W$ 都要乘以 $1-p$，即$Z_1^1=\sum _{i=1}^{100}(0.7{\omega }_1^i)x_1^i=70a$，这样使用 drop_out 的训练集和不使用 drop_out 的测试集的尺度就一致了。所以 drop_out 在训练和测试时是不一样的

代码实现时要注意这点，即训练前要用 train() 函数，表示模型进入训练阶段，该阶段 drop_out 是正常工作的，测试前要用 eval() 函数，表示模型进入测试阶段，drop_out 就会停止工作

1.5. 有效缓解过拟合的原因

• 使用 drop_out 可以使得部分节点失活，可以起到简化神经网络结构的作用，从而起到正则化的作用
• 取平均的策略通常可以有效防止过拟合问题，drop_out 掉不同的隐藏神经元就类似在训练不同的网络，随机删掉部分隐藏神经元导致网络结构已经不同，整个 drop_out 过程就相当于对很多个不同的神经网络取平均
• 使用 drop_out 可以使得神经网络的节点随机失活，这样会让神经网络在训练的时候不会使得某一个节点权重过大，让神经网络的节点不会依赖任何输入的特征

1.6. 代码实现

nn.Dropout 和 nn.functional.dropout 两种具体的实现方法：

class Dropout1(nn.Module):
   def __init__(self):
       super(Dropout1, self).__init__()
       self.fc = nn.Linear(100,20)
 
   def forward(self, input):
       out = self.fc(input)
       out = F.dropout(out, p=0.5, training=self.training)  # 这里必须给traning设置为True
       return out
# 如果设置为F.dropout(out, p=0.5)实际上是没有任何用的, 因为它的training状态一直是默认值False. 由于F.dropout只是相当于引用的一个外部函数, 模型整体的training状态变化也不会引起F.dropout这个函数的training状态发生变化. 所以,在训练模式下out = F.dropout(out) 就是 out = out. 
Net = Dropout1()
Net.train()

#或者直接使用nn.Dropout() (nn.Dropout()实际上是对F.dropout的一个包装, 自动将self.training传入，两者没有本质的差别)
class Dropout2(nn.Module):
  def __init__(self):
      super(Dropout2, self).__init__()
      self.fc = nn.Linear(100,20)
      self.dropout = nn.Dropout(p=0.5)
 
  def forward(self, input):
      out = self.fc(input)
      out = self.dropout(out)
      return out
Net = Dropout2()
Net.train()

---

2. drop_path

2.1. 与 drop_out 的差异

drop_path 将深度学习模型中的多分支结构随机 “失效”，而 drop_out 是对神经元随机 “失效”。换句话说，drop_out 是随机的点对点路径的关闭，drop_path 是随机的点对层之间的关闭

假设有一个 Linear 层输入4结点，输出5结点，那么一共有 20 个点对点路径。drop_out 会随机关闭这些路径，而 drop_path 会随机选择输入结点，使其与之相连的 5 条路径全部关闭

2.2. 工作原理

drop_path 和 drop_out 其实数学原理类似：通过范围是 $(0,1)$ 的随机 rand 值，当施加了一个 drop_rate 后，被关闭的概率 p = rand + drop_rate

• 只需要对 $p$ 进行下取整，即可得到服从 0-1 分布的数据，通过与权重的点乘，即可关闭 drop_rate 比例的结点
• 但是在传播过程中，总结点数没有改变（仍然包含被关闭的结点），因此输入的数据均值$u=sum(x)/N$，就被放大了

假设原始的数据 $X$，结点数为 $N$，均值为 $u$

• 经过比例为 $r$ 的 drop 操作后，总数据有 $n=N\ast r$ 个结点被置 0
• 因此新的均值为 $u^{\prime }=(N-n)\ast u/N$，显然均值发生变化，数据分布以及梯度也随之发生变化
• 为了让数据保持一致性，需要将均值拉回来：$u^{\prime }÷(N-n)/N$，即 $u^{\prime }÷r$
• 但是 drop_path 输出，是对原始数据的调整，通过激活函数来完成 drop 的功能

2.3. 在网络中的应用

假设在前向传播中有如下的代码：

x = x + self.drop_path( self.conv(x) )

那么在 drop_path 分支中，每个 batch 有 drop_prob 的概率样本在 self.conv(x) 不会 “执行”，会以 0 直接传递。

若 $x$ 为输入的张量，其通道为 $[B,C,H,W]$，那么 drop_path 的含义为在一个 batch_size中，随机有 drop_prob 的样本，不经过主干，而直接由分支进行恒等映射

需要注意的是，drop_path 不能直接这样使用：

x = self.drop_path(x)

2.4. 代码实现

def drop_path(x, drop_prob: float = 0., training: bool = False):
    if drop_prob == 0. or not training:
        return x
    keep_prob = 1 - drop_prob
    shape = (x.shape[0],) + (1,) * (x.ndim - 1)  # work with diff dim tensors, not just 2D ConvNets
    random_tensor = keep_prob + torch.rand(shape, dtype=x.dtype, device=x.device)
    random_tensor.floor_()  # binarize
    output = x.div(keep_prob) * random_tensor
    return output


class DropPath(nn.Module):
    """Drop paths (Stochastic Depth) per sample  (when applied in main path of residual blocks).
    """
    def __init__(self, drop_prob=None):
        super(DropPath, self).__init__()
        self.drop_prob = drop_prob

    def forward(self, x):
        return drop_path(x, self.drop_prob, self.training)