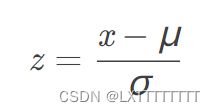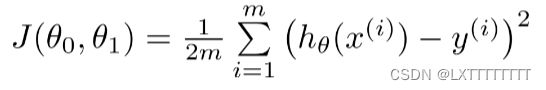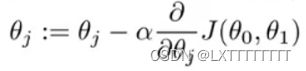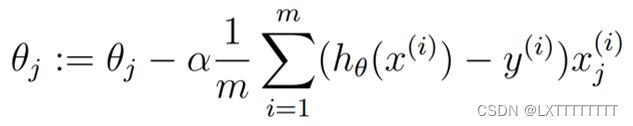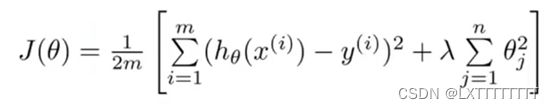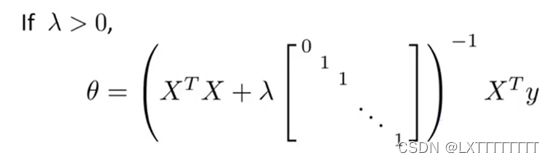机器学习001---线性回归
目录
什么是线性回归?
线性回归基本步骤
数据特征归一化(Feature Normalize)
假设模型(Hypothesis Function)
代价函数(Cost Function)
梯度下降法(Gradient Decent)
正规方程法(Normal Equation)
正则化(Regularization)
比较
总结
线性回归
什么是线性回归?
当我们的数据集提供给我们一组分立的数据时我们使用线性回归的方法拟合出一条曲线使曲线到数据点的距离差异最小。
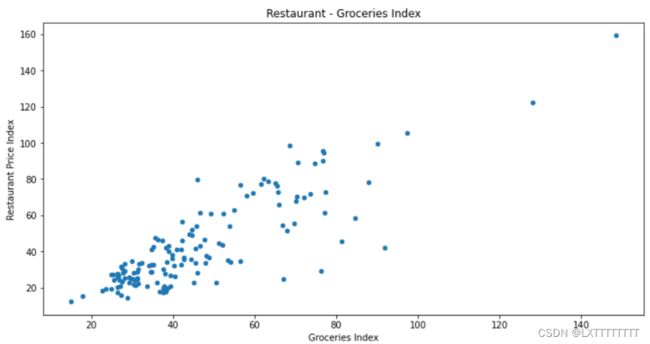 散点图
散点图 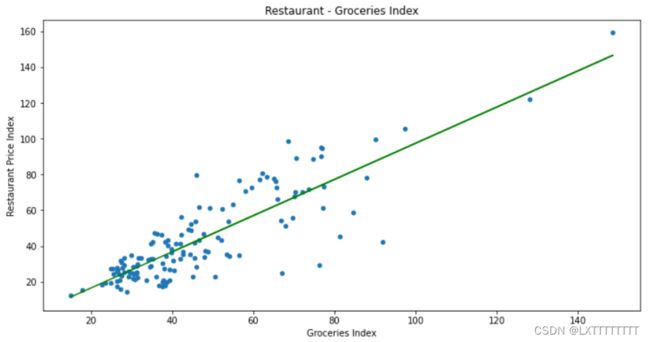 线性回归拟合曲线
线性回归拟合曲线
图为Python线性回归拟合曲线的示例
数据使用Kaggle网站上的cost-of-living-index-2022
线性回归基本步骤
数据特征归一化(Feature Normalize)
通常数据集会提供很多维度的参量,由于这些参量可能会出现数量级差距过大的情况,这会影响算法执行效率,所以通过数据特征归一化来将参量统一至同一数量级。
公式如下:
下为Octave/Matlab描述:
function [X_norm, mu, sigma] = featureNormalize(X)
X_norm = X;
mu = zeros(1, size(X, 2));
sigma = zeros(1, size(X, 2));
mu = mean(X);
sigma = std(X);
X_norm = (X - mu) ./ sigma;
end假设模型(Hypothesis Function)
此处使用一元线性函数来拟合曲线![]() 为预测函数,
为预测函数,![]() 是我们要寻找的目标函数。
是我们要寻找的目标函数。
其中,![]() 可视为一个n + 1维向量
可视为一个n + 1维向量![]() ,n取决于函数的维数,同时将
,n取决于函数的维数,同时将![]() 所对应的参数视为1,参数X也可以视为一个n + 1维向量
所对应的参数视为1,参数X也可以视为一个n + 1维向量![]() ,
,![]() 也可写作以下公式。
也可写作以下公式。
![]()
代价函数(Cost Function)
对于预测函数![]() 我们使用
我们使用![]() 来描述所预测的函数与数据集中实际给出的数据的相似程度,对于
来描述所预测的函数与数据集中实际给出的数据的相似程度,对于![]() 有如下定义
有如下定义
即真实值与预测值之间的距离的均方误差。
![]() 同样有向量化的表达形式,本文不再赘述。
同样有向量化的表达形式,本文不再赘述。
从上述公式可以看出对于代价函数![]() ,
,![]() 的值越小代表拟合程度越高,下文讨论如何降低代价函数。
的值越小代表拟合程度越高,下文讨论如何降低代价函数。
下为Octave/Matlab描述:
function J = computeCost(X, y, theta)
m = length(y);
J = 0;
delta = (X * theta - y) .^ 2;
J = 1 / (2 * m) * sum(delta);
end
梯度下降法(Gradient Decent)
对![]() 各参量
各参量![]() 求偏导,可得出
求偏导,可得出![]() 在此时的梯度,使
在此时的梯度,使![]() 沿梯度方向下降可使
沿梯度方向下降可使![]() 收敛于局部最小值(若存在收敛点)。公式如下。
收敛于局部最小值(若存在收敛点)。公式如下。
对偏导数化简得:
注意:此时下降时对n + 1维![]() 要同时下降,否则会影响下降结果。
要同时下降,否则会影响下降结果。
其中,![]() 为下降的“步长”,对于不同的实际问题,要恰当的选择
为下降的“步长”,对于不同的实际问题,要恰当的选择![]() ,若
,若![]() 过小则下降效率会过低,若
过小则下降效率会过低,若![]() 过大则有可能会在下降的过程中“错过”收敛点甚至会转变为发散的状态。
过大则有可能会在下降的过程中“错过”收敛点甚至会转变为发散的状态。
值得注意的是,我们在恰当选取![]() 之后在下降的过程之中无需调整
之后在下降的过程之中无需调整![]() 的取值,因为在整个代价函数趋于收敛的过程之中,对应的偏导数会逐渐下降,
的取值,因为在整个代价函数趋于收敛的过程之中,对应的偏导数会逐渐下降,![]() 与偏导数的乘积也会逐渐下降,从而达到一种逐渐降低“步长”的效果。
与偏导数的乘积也会逐渐下降,从而达到一种逐渐降低“步长”的效果。
下为Octave/Matlab描述:
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
m = length(y);
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
theta = theta - alpha / m * X' * (X * theta - y);
J_history(iter) = computeCost(X, y, theta);
end
end
同样的,我们对梯度下降的函数进行正则化修正,结果如下:
正规方程法(Normal Equation)
正规方程法,区别于梯度下降法所用的迭代思想,可以说是一步到位可以求得![]() 的收敛点。对于矩阵相乘形式的
的收敛点。对于矩阵相乘形式的![]() 与
与![]() , 将m组参数x
, 将m组参数x![]() 视为一个m * (n + 1)维向量X ,对于
视为一个m * (n + 1)维向量X ,对于![]() 中求偏导的部分,采用向量化矩阵化的思想得到最后结果如下:
中求偏导的部分,采用向量化矩阵化的思想得到最后结果如下:
下为Octave/Matlab描述:
function [theta] = normalEqn(X, y)
theta = zeros(size(X, 2), 1);
theta = pinv( X' * X ) * X' * y;
end
正则化(Regularization)
正则化是为了避免过拟合的问题,为了解决这个问题我们对代价函数进行部分修正,在原函数的结尾加上惩罚项,公式如下:
可以看出,公式的前半部分就是之前所提到的公式,后面加上的则是惩罚项,![]() 为惩罚的强度,若
为惩罚的强度,若![]() 过小则会出现惩罚不足的情况,所以
过小则会出现惩罚不足的情况,所以![]() 通常设为1。
通常设为1。
同样的,我们对梯度下降法以及正规方程法进行同样的修正:
![]()
下为Octave/Matlab描述:
function [J, grad] = costFunctionReg(theta, X, y, lambda)
m = length(y);
J = 0;
grad = zeros(size(theta));
X_ori = X;
X = X * theta;
theta1 = [0;theta(2:end)];
J = (-1) / m * sum(y .* log(X) + (1 - y) .* log(1 - X)) + lambda / (2 * m) * theta1' * theta1;
grad = 1 / m * X_ori' * (X - y) + lambda / m * theta1;
end
比较
对于梯度下降法和正规方程法这两者在数据集不同时需灵活选取方法,此二者优劣如下。
梯度下降:
优点:
1.当维数较大时(>1e6)计算效果较好。
缺点:
1.需适当且合理地选取![]() 。
。
2.需要迭代多代。
正规方程:
优点:
1.可以”一步到位“。
缺点:
1.在维数较低时(<1e6)计算效果较好。
2.由于公式中需要计算逆矩阵,所以在维数较大时效果较差。
总结
线性回归是针对于线性的数据集效果较好的一种算法,其较为易于理解,并且是很多非线性问题的基础思想,但是其对于非线性数据或者是高度复杂的数据较为难以描述。