聚类算法KMeans
文章目录
- 前言
- 一、KMeans
-
- 1.1 KMeans是如何工作的
- 1.2 簇内误差平方和
- 1.3 KMeans算法的时间复杂度
- 二、sklearn.cluster.KMeans
-
- 2.1 重要参数n_clusters
-
- 2.1.1 设计一次聚类
-
- 2.1.1.1 导入包并且创建数据集
- 2.1.1.2 分别画出样本的带颜色和不带颜色的数据分布
- 2.1.1.3 基于这个分布来进行KMeans聚类
- 2.1.1.4 KMeans什么时候使用labels什么时候使用predict
- 2.1.1.5 重要属性cluster_centers_,查看质心
- 2.1.1.6 重要属性inertia_,查看总距离平方和
- 2.1.1.7 画通过KMeans聚类之后的图像
- 2.1.1.8 看不同n_clusters下的kmean的表现
- 2.1.2 聚类算法的模型评估指标
-
- 2.1.2.1 当真实标签已知的时候(在真实情况中基本不会发生)
- 2.1.2.2 当真实标签未知的时候:轮廓系数
- 2.1.2.3 当真实标签未知的时候:Calinski-Harabaz Index
- 2.1.3 案例:基于轮廓系数来选择n_clusters
-
- 1.导入库
- 2. 设置画布
- 3. 建模,画图的数据的准备
- 4. 绘制子图1,看分簇轮廓系数柱状图
- 5. 绘制子图2,每个样本的散点分布图及质心
- 6. 对不同的分簇个数画图来进行选择n_clusters(对上面的步骤的合并,虽然看着很多,但是很多都是和上面一样注释,在这里就是助于理解)
- 7. 根据上图总结
- 2.2 重要参数init & random_state & n_init:初始质心怎么放好?
- 2.3 重要参数max_iter & tol:让迭代停下来
- 2.4 重要属性与重要接口
- 2.5 函数cluster.k_means
- 总结
前言
虽然代码很常很长,但是都是进行理解的注释
一、KMeans
KMeans可以说是最简单的聚类算法没有之一
1.1 KMeans是如何工作的
关键概念:簇与质心
- KMeans算法将一组N个样本的特征矩阵X划分为K个无交集的簇,直观上来看是簇是一组一组聚集在一起的数据,在一个簇中的数据就认为是同一类。簇就是聚类的结果表现。
- 簇中所有数据的均值 μ i \mu_i μi 通常被称为这个簇的“质心”(centroids)。在一个二维平面中,一簇数据点的质心的横坐标就是这一簇数据点的横坐标的均值,质心的纵坐标就是这一簇数据点的纵坐标的均值。同理可推广至高维空间。
在KMeans算法中,簇的个数K是一个超参数,需要我们人为输入来确定。KMeans的核心任务就是根据我们设定好的K,找出K个最优的质心,并将离这些质心最近的数据分别分配到这些质心代表的簇中去。具体过程可以总结如下:

当我们找到一个质心,在每次迭代中被分配到这个质心上的样本都是一致的,即每次新生成的簇都是一致的,所有的样本点都不会再从一个簇转移到另一个簇,质心就不会变化了。
这个过程在可以由下图来显示,我们规定,将数据分为4簇(K=4),其中白色X代表质心的位置:

1.2 簇内误差平方和
被分在同一个簇中的数据是有相似性的,而不同簇中的数据是不同的
当聚类完毕之后,我们就要分别去研究每个簇中的样本都有什么样的性质,从而根据业务需求制定不同的商业或者科技策略。这个听上去和评分卡案例讲解的“分箱”概念有些类似,即我们分箱的目的是希望,一个箱内的人有着相似的信用风险,而不同箱的人的信用风险差异巨大,以此来区别不同信用度的人,因此我们追求“组内差异小,组间差异大”。聚类算法也是同样的目的,我们追求“簇内差异小,簇外差异大”。而这个“差异“,由样本点到其所在簇的质心的距离来衡量。
对于一个簇来说,所有样本点到质心的距离之和越小,我们就认为这个簇中的样本越相似,簇内差异就越小。而距离的衡量方法有多种:
欧 几 里 得 距 离 : d ( x , μ ) = ∑ i = 1 n ( x i − μ i ) 2 欧几里得距离:d(x,\mu)=\sqrt{\sum_{i=1}^{n}(x_i-\mu_i)^2} 欧几里得距离:d(x,μ)=i=1∑n(xi−μi)2
曼 哈 顿 距 离 : d ( x , μ ) = ∑ i = 1 n ( ∣ x i − μ ∣ ) 曼哈顿距离:d(x,\mu)=\sum_{i=1}^{n}(|x_i-\mu|) 曼哈顿距离:d(x,μ)=i=1∑n(∣xi−μ∣)
余 弦 距 离 : cos θ = ∑ i = 1 n ( x i ∗ μ ) ∑ i = 1 n ( x i ) 2 ∗ ∑ i = 1 n ( μ ) 2 余弦距离:\cos\theta=\frac{\sum_{i=1}^{n}(x_i*\mu)}{\sqrt{\sum_{i=1}^{n}(x_i)^2}*\sqrt{\sum_{i=1}^{n}(\mu)^2}} 余弦距离:cosθ=∑i=1n(xi)2∗∑i=1n(μ)2∑i=1n(xi∗μ)
- x : x: x:簇中的一个样本点
- μ : \mu: μ:该簇中的质心
- n : n: n:示每个样本点中的特征数目
- i : i: i:组成点 x x x的每个特征
如我们采用欧几里得距离,则一个簇中所有样本点到质心的距离的平方和为:
C l u s t e r S u m o f S q u a r e ( C S S ) = ∑ j = 0 m ∑ i = 1 n ( x i − μ i ) 2 Cluster~Sum~of~Square~(CSS)=\sum_{j=0}^{m}\sum_{i=1}^{n}(x_i-\mu_i)^2 Cluster Sum of Square (CSS)=j=0∑mi=1∑n(xi−μi)2
T o t a l C l u s t e r S u m o f S q u a r e = ∑ l = 1 k C S S l Total~Cluster~Sum~of~Square=\sum_{l=1}^{k}CSS_l Total Cluster Sum of Square=l=1∑kCSSl
- m : m: m:为一个簇中样本的个数
- j : j: j:每个样本的编号
这个公式被称为簇内平方和(cluster Sum of Square),又叫做Inertia。而将一个数据集中的所有簇的簇内平方和相加,就得到了整体平方和(Total Cluster Sum ofSquare),又叫做total inertia。Total Inertia越小,代表着每个簇内样本越相似,聚类的效果就越好。
KMeans追求的是,求解能够让Inertia最小化的质心。
在质心不断变化不断迭代的过程中,总体平方和是越来越小的。我们可以使用数学来证明,当整体平方和最小的时候,质心就不再发生变化了。如此,K-Means的求解过程,就变成了一个最优化问题。
在KMeans中,我们在一个固定的簇数K下,最小化总体平方和来求解最佳质心,并基于质心的存在去进行聚类。这与逻辑回归中最小化损失函数的过程十分相似,并且,整体距离平方和的最小值其实可以使用梯度下降来求解。
KMeans有损失函数吗
-
在逻辑回归中曾有这样的结论:损失函数本质是用来衡量模型的拟合效果的,只有有着求解参数需求的算法,才会有损失函数。
Kmeans不求解什么参数,它的模型本质也没有在拟合数据,而是在对数据进行一种探索,Inertia更像是Kmeans的模型评估指标,而非损失函数。
-
对比来看,在决策树中,我们有衡量分类效果的指标准确度accuracy,准确度所对应的损失叫做泛化误差,但我们不能通过最小化泛化误差来求解某个模型中需要的信息,我们只是希望模型的效果上表现出来的泛化误差很小。因此决策树,KNN等算法,是绝对没有损失函数的。
Inertia是基于欧几里得距离的计算公式得来的。实际上,我们也可以使用其他距离,每个距离都有自己对应的Inertia。在Kmeans中,只要使用了正确的质心和距离组合,无论使用什么样的距离,都可以达到不错的聚类效果:

而这些组合,由严格的数学证明来推导。在sklearn当中,我们无法选择使用的距离,只能使用欧式距离。因此,我们也无需去担忧这些距离所搭配的质心选择是如何得来的了。
1.3 KMeans算法的时间复杂度
除了模型本身的效果之外,我们还使用另一种角度来度量算法:算法复杂度。
算法的复杂度分为时间复杂度和空间复杂度,时间复杂度是指执行算法所需要的计算工作量,常用大O符号表述;而空间复杂度是指执行这个算法所需要的内存空间。
如果一个算法的效果很好,但需要的时间复杂度和空间复杂度都很大,那我们将会权衡算法的效果和所需的计算成本之间。
和KNN一样,KMeans算法是一个计算成本很大的算法。
KMeans算法的平均复杂度是O(knT),其中k是我们的超参数,所需要输入的簇数,n是整个数据集中的样本量,T是所需要的迭代次数(相对的,KNN的平均复杂度是O(n))。在最坏的情况下,KMeans的复杂度可以写作 O ( n ( k + 2 ) / p ) O(n^{(k+2)/p}) O(n(k+2)/p),其中n是整个数据集中的样本量,p是特征总数。
比起其他聚类算法,k-means算法已经快了,但它一般找到Inertia的局部最小值。 这就是为什么多次
重启它会很有用。
二、sklearn.cluster.KMeans
class sklearn.cluster.KMeans (n_clusters=8, init=’k-means++’, n_init=10, max_iter=300, tol=0.0001,
precompute_distances=’auto’, verbose=0, random_state=None, copy_x=True, n_jobs=None, algorithm=’auto’)
2.1 重要参数n_clusters
n_clusters是KMeans中的k,表示着我们告诉模型我们要分几类。这是KMeans当中唯一一个必填的参数,默认为8类,但通常我们的聚类结果会是一个小于8的结果。通常,在开始聚类之前,我们并不知道n_clusters究竟是多少,因此我们要对它进行探索。
2.1.1 设计一次聚类
当我们拿到一个数据集,如果可能的话,我们希望能够通过绘图先观察一下这个数据集的数据分布,以此来为我们聚类时输入的n_clusters做一个参考。
首先,我们来自己创建一个数据集。这样的数据集是我们自己创建,所以是有标签的(正常拿到的数据99%是不会有标签的)。
2.1.1.1 导入包并且创建数据集
from sklearn.datasets import make_blobs #创建数据集
import matplotlib.pyplot as plt
#500条数据,每个数据2个特征,4个质心也就是分为4个簇,设置随机参数
X,y = make_blobs(n_samples=500,n_features=2,centers=4,random_state=1)
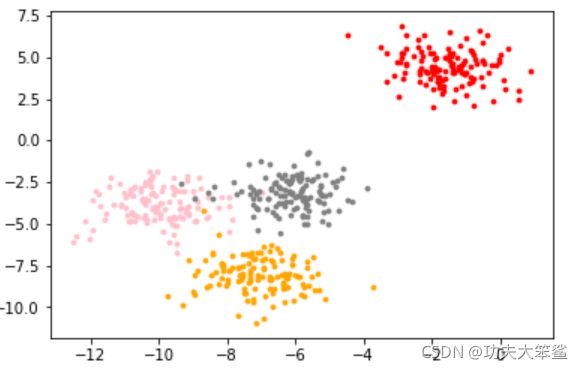
2.1.1.2 分别画出样本的带颜色和不带颜色的数据分布
因为是自己创建的数据集,所以是存在标签的,也就是说数据集是已经被分好的,在这里带颜色的图就是sklearn创建的标签的分布,在这里我们打印出带有颜色和不低啊有颜色的来进行观察
fig,axl = plt.subplots(1)
axl.scatter(X[:,0],X[:,1]
,marker='o' #点的形状
,s=8#点的大小
)
plt.show()
color = ['red','pink','orange','gray']
fig,axl = plt.subplots(1)
for i in range(4):
axl.scatter(X[y==i,0],X[y==i,1]
,marker='o'
,s=8
,color=color[i]
)
plt.show()
2.1.1.3 基于这个分布来进行KMeans聚类
from sklearn.cluster import KMeans #KMeans
#通过上面的分布图假设分为3簇
n_clusters = 3
cluster = KMeans(n_clusters=n_clusters,random_state=0).fit(X)
#重要属性labels_,查看聚好的类别,每个样本所对应的类
y_pred = cluster.labels_
y_pred
#KMeans因为并不需要建立模型或者预测结果,因此我们只需要fit就能够得到聚类结果了
#KMeans也有接口predict和fit_predict,表示学习数据X并对X的类进行预测
#但所得到的结果和我们不调用predict,直接fit之后调用属性labels一模一伴
pre = cluster.fit_predict(X)
pre
#使用labels和predict得到的结果是相同的
pre == y_pred
2.1.1.4 KMeans什么时候使用labels什么时候使用predict
当数据量太大的时候需要predic,其实我们不必使用所有的数据来寻找质心,少量的数据就可以帮助我们确定质心了当我们数据量非常大的时候,我们可以使用部分数据来帮助我们确认质心剩下的数据的聚类结果,使用predict来调用
#假设这个数据非常大,选250条数据进行训练
cluster_smallsub = KMeans(n_clusters=n_clusters, random_state=0).fit(X[:250])
#使用predict
y_pred_ = cluster_smallsub.predict(X)
y_pred_
但从运行得出这样的结果,肯定与直接fit全部数据会不一致。有时候,当我们不要求那么精确,或者我们的数据量实在太大,那我们可以使用这种方法,使用接口predict
如果数据量还行,不是特别大,直接使用fit之后调用属性.labels_提出来
#可以看到得出的结果和fit全部x是不同的
y_pred == y_pred_
2.1.1.5 重要属性cluster_centers_,查看质心
#重要属性cLuster_centers_,查看质心
centroid = cluster.cluster_centers_
centroid
centroid.shape
2.1.1.6 重要属性inertia_,查看总距离平方和
#重要属性inertia_,查看总距离平方和
inertia = cluster.inertia_
inertia
2.1.1.7 画通过KMeans聚类之后的图像
color = ["red","pink","orange","gray"]
fig,axl = plt.subplots(1)
#n_clusters在开始定义是3
for i in range(n_clusters):
axl.scatter(X[y_pred==i,0],X[y_pred==i,1]
,marker='o'
,s=8
,c=color[i]
)
#画出质心
axl.scatter(centroid[:,0],centroid[:,1]
,marker='x'
,s=8
,c='black')
plt.show()
2.1.1.8 看不同n_clusters下的kmean的表现
- 等于4的时候
#如果我们把猜测的羡数换成4,Inertia会怎么样?
n_clusters = 4
cluster_ = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
#总距离平方和
inertia_ = cluster_.inertia_
inertia_
- 等于5的时候
n_clusters = 5
cluster_ = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
inertia_ = cluster_.inertia_
inertia_
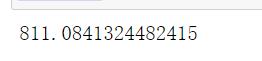
- 等于500的时候
n_clusters = 500
cluster_ = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
inertia_ = cluster_.inertia_
inertia_
![]()
可以看到,随着n_clusters的增大,发现总距离平方和不断减少,当n_clusters为500的时候,总距离平方和竟然为0,原因是总距离平方和是样本在相同簇内其他样本来求取得到的,所以会随着n_clusters越大,就越小,我们不能以n_clusters来作为评判标准,在下面会介绍相应的模型评估标准
2.1.2 聚类算法的模型评估指标
不同于分类模型和回归,聚类算法的模型评估不是一件简单的事。在分类中,有直接结果(标签)的输出,并且分类的结果有正误之分,所以我们使用预测的准确度,混淆矩阵,ROC曲线等等指标来进行评估,但无论如何评估,都是在”模型找到正确答案“的能力。而回归中,由于要拟合数据,我们有SSE均方误差,有损失函数来衡量模型的拟合程度。但这些衡量指标都不能够使用于聚类。
聚类模型的结果不是某种标签输出,并且聚类的结果是不确定的,其优劣由业务需求或者算法需求来决定,并且没有永远的正确答案。
如何衡量聚类的效果
KMeans的目标是确保“簇内差异小,簇外差异大”,我们就可以通过衡量簇内差异来衡量聚类的效果。前面提到过,Inertia是用距离来衡量簇内差异的指标,Inertia越小模型越好,因此,我们是否可以使用Inertia来作为聚类的衡量指标呢?
-
可以,但是这个指标的缺点和极限太大。
-
它不是有界的。我们只知道,Inertia是越小越好,是0最好,但我们不知道,一个较小的Inertia究竟有没有达到模型的极限,能否继续提高。
-
它的计算太容易受到特征数目的影响,数据维度很大的时候,Inertia的计算量会陷入维度诅咒之中,计算量会爆炸,不适合用来一次次评估模型。
-
它会受到超参数K(n_clusters)的影响,在我们之前的常识中其实我们已经发现,随着K越大,Inertia注定会越来越小,但这并不代表模型的效果越来越好了
-
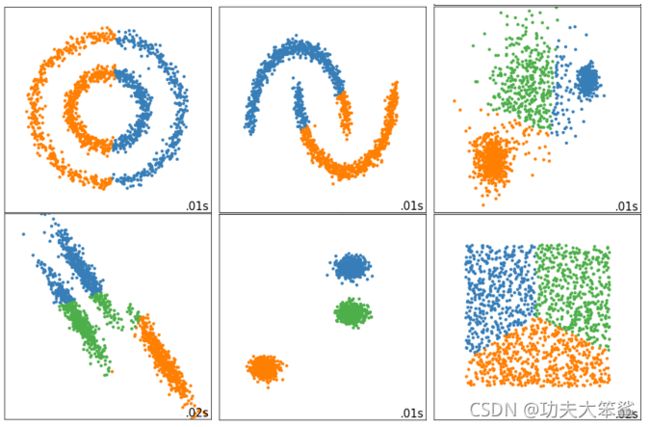
Inertia对数据的分布有假设,它假设数据满足凸分布(即数据在二维平面图像上看起来是一个凸函数的样子),并且它假设数据是各向同性的(isotropic),即是说数据的属性在不同方向上代表着相同的含义。但是现实中的数据往往不是这样。所以使用Inertia作为评估指标,会让聚类算法在一些细长簇,环形簇,或者不规则形状的流形时表现不佳:
2.1.2.1 当真实标签已知的时候(在真实情况中基本不会发生)
虽然我们在聚类中不输入真实标签,但这不代表我们拥有的数据中一定不具有真实标签,或者一定没有任何参考信息。当然,在现实中,拥有真实标签的情况非常少见(几乎是不可能的)。如果拥有真实标签,我们更倾向于使用分类算法。但不排除我们依然可能使用聚类算法的可能性。如果我们有样本真实聚类情况的数据,我们可以对于聚类算法的结果和真实结果来衡量聚类的效果。常用的有以下三种方法:

三种方法的共同点是都是评分越高效果就越好,放入kmeans聚类出来的标签与原标签,来获得相应的分数进行评判效果
2.1.2.2 当真实标签未知的时候:轮廓系数
在99%的情况下,我们是对没有真实标签的数据进行探索,也就是对不知道真正答案的数据进行聚类。这样的聚类,是完全依赖于评价簇内的稠密程度(簇内差异小)和簇间的离散程度(簇外差异大)来评估聚类的效果。其中轮廓系数是最常用的聚类算法的评价指标。它是对每个样本来定义的,它能够同时衡量:
- 样本与其自身所在的簇中的其他样本的相似度a,等于样本与同一簇中所有其他点之间的平均距离
- 样本与其他簇中的样本的相似度b,等于样本与下一个最近的簇中的所有点之间的平均距离
根据聚类的要求”簇内差异小,簇外差异大“,我们希望b永远大于a,并且大得越多越好。
单个样本的轮廓系数计算为:
s = b − a max ( a , b ) s=\frac{b-a}{\max(a,b)} s=max(a,b)b−a
这个公式可以被解析为:
f ( n ) = { 1 − a / b , if a < b 0 , if a = b b / a − 1 if a > b f(n)= \begin{cases} 1-a/b, & \text {if $a
很容易理解轮廓系数范围是(-1,1)
- 值越接近1表示样本与自己所在的簇中的样本很相似,并且与其他簇中的样本不相似。
- 当样本点与簇外的样本更相似的时候,轮廓系数就为负。
- 当轮廓系数为0时,则代表两个簇中的样本相似度一致,两个簇本应该是一个簇。
如果一个簇中的大多数样本具有比较高的轮廓系数,则簇会有较高的总轮廓系数,则整个数据集的平均轮廓系数越高,则聚类是合适的。如果许多样本点具有低轮廓系数甚至负值,则聚类是不合适的,聚类的超参数K可能设定得太大或者太小。
在sklearn中:
- 模块metrics中的类silhouette_score来计算轮廓系数,它返回的是一个数据集中,所有样本的轮廓系数的均值。
- 在metrics模块中的silhouette_sample,它的参数与轮廓系数一致,但返回的是数据集中每个样本自己的轮廓系数。
from sklearn.metrics import silhouette_score #所有样本的轮廓系数均值
from sklearn.metrics import silhouette_samples #每个样本自己的轮廓系数
#y_pred是上面.labels_得出来的
silhouette_score(X,y_pred)
#返回每个样本的轮廓系数
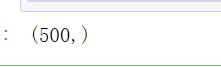
silhouette_samples(X,y_pred).shape
#返回了500个,也就是每一个样本都计算了一个轮廓系数
#运行上面的分为4簇的cluster_
silhouette_score(X,cluster_.labels_)
#运行上面的分为5簇的cluster_,发现降低了,说明这个并不是随着n_clusters增大而增大
silhouette_score(X,cluster_.labels_)
轮廓系数有很多优点,它在有限空间中取值,使得我们对模型的聚类效果有一个“参考”。并且,轮廓系数对数据的分布没有假设,因此在很多数据集上都表现良好。但它在每个簇的分割比较清洗时表现最好。但轮廓系数也有缺陷,它在凸型的类上表现会虚高,比如基于密度进行的聚类,或通过DBSCAN获得的聚类结果,如果使用轮廓系数来衡量,则会表现出比真实聚类效果更高的分数。
2.1.2.3 当真实标签未知的时候:Calinski-Harabaz Index
除了轮廓系数是最常用的,我们还有卡林斯基-哈拉巴斯指数(Calinski-Harabaz Index,简称CHI,也被称为方差比标准),戴维斯-布尔丁指数(Davies-Bouldin) 以及 权变矩阵(Contingency Matrix) 可以使用。
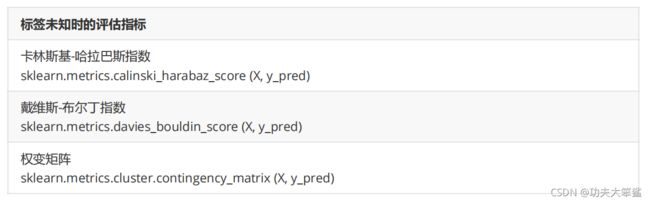
重点来了解一下卡林斯基-哈拉巴斯指数。Calinski-Harabaz指数越高越好。对于有k个簇的聚类而言,Calinski-Harabaz指数s(k)写作如下公式:
s ( k ) = T r ( B k ) T r ( W k ) ∗ N − k k − 1 s(k)=\frac{Tr(B_k)}{Tr(W_k)}*\frac{N-k}{k-1} s(k)=Tr(Wk)Tr(Bk)∗k−1N−k
- N : N: N:数据集中的样本量
- k : k: k:簇的个数(即类别的个数)
- B k : B_k: Bk:组间离散矩阵,即不同簇之间的协方差矩阵
- W k : W_k: Wk:簇内离散矩阵,即一个簇内数据的协方差矩阵
- T r : Tr: Tr:矩阵的迹。在线性代数中,一个n×n矩阵A的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵A的迹(或迹数),一般记作 T r ( A ) Tr(A) Tr(A)。
数据之间的离散程度越高,协方差矩阵的迹就会越大。
组内离散程度低,协方差的迹就会越小, T r ( W k ) Tr(W_k) Tr(Wk)也就越小,同时,组间离散程度大,协方差的的迹也会越大, T r ( B k ) Tr(B_k) Tr(Bk)就越大,这正是我们希望的,因此Calinski-harabaz指数越高越好。
from sklearn.metrics import calinski_harabasz_score #CHI
#y_pred时经过KMeans训练之后的分簇聚类
calinski_harabasz_score(X, y_pred)
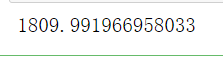
虽然calinski-Harabaz指数没有界,在凸型的数据上的聚类也会表现虚高。但是比起轮廓系数,它有一个巨大的优点,就是计算非常快速。之前使用过魔法命令%%timeit来计算一个命令的运算时间,今天我们来选择另一种方法:时间戳计算运行时间。
from time import time
#使用CHI的运行时间
t0 = time()
calinski_harabasz_score(X, y_pred)
time() - t0
> 0.000997304916381836
#使用轮廓系数的运行时间
t0 = time()
silhouette_score(X,y_pred)
time() - t0
> 0.00795125961303711
#将时间戳转为时间
import datetime
datetime.datetime.fromtimestamp(t0).strftime("%Y-%m-%d %H:%M:%S")
>'2021-11-18 21:34:00'
#运行时间大概是7倍左右
0.00795125961303711//0.000997304916381836=7.0
2.1.3 案例:基于轮廓系数来选择n_clusters
我们通常会绘制轮廓系数分布图和聚类后的数据分布图来选择我们的最佳n_clusters。
1.导入库
from sklearn.cluster import KMeans #KMeans聚类算法
from sklearn.metrics import silhouette_samples, silhouette_score #每个样本的轮廓系数 和 所有样本的平均轮廓系数
import matplotlib.pyplot as plt
import matplotlib.cm as cm #colormap 可以使用特定的小数来代表一种颜色
import numpy as np
import pandas as pd
2. 设置画布
基于轮廓系数来找到最佳的n_clusters
知道每个聚出来的类的轮廓系数是多少,还要与各个类之间的轮廓系数的对比
知道聚类后的分布是什么样的
#先设定我们要分的簇数
n_clusters = 4
#创建一个画布,一行两列
fig, (ax1,ax2) = plt.subplots(1,2)
#设置画布尺寸,在这里也就是两个画板都是宽为9高为7
fig.set_size_inches(18,7)
#第一个图是轮廓系数图像,是由各个簇的轮廓系数组成的横向条形图
#横向条形图的横坐标是轮廓系数的取值,纵坐标是样本
#首先来设置横坐标
#轮廓系数的取值是(-1,1),但是我们希望的轮廓系数是大于0的,小于0的证明分的不好
#太长的横坐标不利于可视化,所以取(-0.1,1)这个范围
ax1.set_xlim([-0.1,1])
#纵坐标来说从0开始,最大值是X.shape[0],就是样本的个数
#我们让每个簇的排在一起,不同簇之间有空隙
#在设置纵坐标的范围的时候,在X.shape[0]的基础上,加上一个距离(n_clusters+1)*10来当做间隔使用
#这里+1的原因是让所画的图不仅是柱与柱之间有间隙,要与x轴和最上面都要有间隙
ax1.set_ylim([0, X.shape[0]+(n_clusters + 1)*10])
3. 建模,画图的数据的准备
#开始建模,查看聚类好的标签
clusterer = KMeans(n_clusters=n_clusters,random_state=10).fit(X)
clusterer_labels = clusterer.labels_
#聚类好的结果
clusterer_labels
#调用轮廓系数分数,silhouette_score是计算总样本的轮廓系数的均值
#需要输入的是特征矩阵X和聚类完之后的标签
silhouette_avg = silhouette_score(X,clusterer_labels)
#打印在不同的n_clusters下,整体的轮廓系数
print(f'n_clusters的取值为{n_clusters}, 样本整体的平均轮廓系数是{silhouette_avg}')
#silhouette_samples返回每个样本的轮廓系数来当做x轴的取值
sample_silhouette_values = silhouette_samples(X,clusterer_labels)
sample_silhouette_values.shape
4. 绘制子图1,看分簇轮廓系数柱状图
#设置一个y轴的初始值,因为不希望画的图像是贴在x轴的,要和x轴保持一些距离
y_lower = 10
#接下来对每一个簇都进行循环
for i in range(n_clusters):
#在获得的每个样本的轮廓系数中抽取出属于第i簇的轮廓系数,并且需要进行排序
#因为排序之后的图像看着就像是递增或递减,更能直观的观察
#sample_silhouette_values是轮廓系数,clusterer_labels是每个样本的分簇,clusterer_labels == i就是取出第i簇的轮廓系数
ith_cluster_silhouette_values = sample_silhouette_values[clusterer_labels == i]
#会改掉原数据的顺序
ith_cluster_silhouette_values.sort()
#这个簇的样本数是多少
size_cluster_i = ith_cluster_silhouette_values.shape[0]
#这个簇在y轴上面的取值,应该从y_lower开始作为最小值,从初始加上这个簇中样本的数量为结束值
y_upper = y_lower + size_cluster_i
#在colormap库中,使用小数来调用颜色
#在nipy_spectral([输入任意小数来代表一个颜色])
#在这里希望的是每个簇的颜色是不同的,需要的颜色种类就是分簇的个数
#使用这个可以确保不同的簇有不同的颜色,只要小数是确定的,颜色就不会改变
#不一定是这种除法,只要保证是小数,而且相同簇的小数是相同的即可
color = cm.nipy_spectral(float(i)/n_clusters)
#开始填充子图1中的内容
#fill_between 是让一个范围中的柱状图都显示统一颜色的函数
#fill_betweenx 的范围是在纵坐标上
#fill_betweeny 的范围是在横坐标上
#fill_betweenx 的参数应该输入(纵坐标的下限,纵坐标的上限,对应横坐标的取值,柱状图的颜色)
ax1.fill_betweenx(np.arange(y_lower,y_upper)
,ith_cluster_silhouette_values
,facecolor=color
,alpha=0.7)
#为每一个簇的轮廓系数写上编号,并且让编号显示在坐标轴的每个条形图中间的位置
#text的参数为(要显示编号的位置的横坐标,要显示编号的位置的纵坐标,要显示的编号内容)
ax1.text(-0.05 #为了不在0的位置显示,所以在-0.05,这样就可以空出来了
,y_lower + 0.5*size_cluster_i #取得一个簇的样本数的中间值作为编号的存放位置
,str(i))
#为下一个簇计算新的y轴上面的初始值,是每一次迭代之后,y的上限在加上10
#以此来保证,下一次的簇不会覆盖上一次的簇并且不同簇之间是有空隙的
#这里的价10是因为在最上面设置的y的初始值为10,就代表每个空隙都要是10
y_lower = y_upper + 10
#对子图1设置标题,x轴的名字,y轴的名字
ax1.set_title("The silhouette plot for the various clusters.")
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
#将总样本的平均轮廓系数用虚线在子图里画出来,方便进行比对
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
#设置y轴不显示刻度
ax1.set_yticks([])
#设置x轴的取值范围
ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
5. 绘制子图2,每个样本的散点分布图及质心
#对第二个子图进行处理,首先获取颜色,这里的颜色要和上面画子图一时候每个簇对应的颜色相同,这就是使用colormap的原因
#所以颜色对应的小数的计算方法要和画子图1的时候要相同
#所以使用最开始得到的聚类结果转为float来进行计算
colors = cm.nipy_spectral(clusterer_labels.astype(float) / n_clusters)
colors
#画散点图,和上面的《第一次聚类》中一样
ax2.scatter(X[:,0],X[:,1]
,marker='o'
,s=8
,c=colors)
#获得每个簇中的质心
centers = clusterer.cluster_centers_
centers
#将质心添加到散点图里
ax2.scatter(centers[:,0],centers[:,1]
,marker='x'
,s=200
,c='red'
,alpha=1)
#对子图2设置标题
ax2.set_title("The visualization of the clustered data.")
ax2.set_xlabel("Feature space for the 1st feature")
ax2.set_ylabel("Feature space for the 2nd feature")
#设置fig的总标题
fig.suptitle(("Silhouette analysis for KMeans clustering on sample data"
"with n_clusters = %d" % n_clusters),
fontsize=14, fontweight='bold'#使用粗体
)
plt.show()
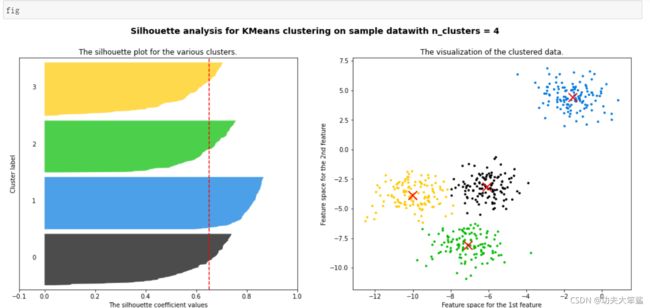
可以看出,分的簇蓝色的是最好的,基本所有都过了平均线,总体上来说还是不错的,每个簇都有一些过了平均线
都对轮廓系数有了贡献,小于平均线的可以看成是拖后腿的,对于这种分簇来说还是非常不错的
6. 对不同的分簇个数画图来进行选择n_clusters(对上面的步骤的合并,虽然看着很多,但是很多都是和上面一样注释,在这里就是助于理解)
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
for n_clusters in [2,3,4,5,6,7]:
#先设定我们要分的簇数
n_clusters = n_clusters
#创建一个画布,一行两列
fig, (ax1,ax2) = plt.subplots(1,2)
#设置画布尺寸,在这里也就是两个画板都是宽为9高为7
fig.set_size_inches(18,7)
#第一个图是轮廓系数图像,是由各个簇的轮廓系数组成的横向条形图
#横向条形图的横坐标是轮廓系数的取值,纵坐标是样本
#首先来设置横坐标
#轮廓系数的取值是(-1,1),但是我们希望的轮廓系数是大于0的,小于0的证明分的不好
#太长的横坐标不利于可视化,所以取(-0.1,1)这个范围
ax1.set_xlim([-0.1,1])
#纵坐标来说从0开始,最大值是X.shape[0],就是样本的个数
#我们让每个簇的排在一起,不同簇之间有空隙
#在设置纵坐标的范围的时候,在X.shape[0]的基础上,加上一个距离(n_clusters+1)*10来当做间隔使用
ax1.set_ylim([0, X.shape[0]+(n_clusters + 1)*10])
#开始建模,查看聚类好的标签
clusterer = KMeans(n_clusters=n_clusters, random_state=10).fit(X)
cluster_labels = clusterer.labels_
#调用轮廓系数分数,silhouette_score是计算总样本的轮廓系数的均值
#需要输入的是特征矩阵X和聚类完之后的标签
silhouette_avg = silhouette_score(X, cluster_labels)
#打印在不同的n_clusters下,整体的轮廓系数
print(f'n_clusters的取值为{n_clusters}, 样本整体的平均轮廓系数是{silhouette_avg}')
#silhouette_samples返回每个样本的轮廓系数来当做x轴的取值
sample_silhouette_values = silhouette_samples(X, cluster_labels)
#设置一个y轴的初始值,因为不希望画的图像是贴在x轴的,要和x轴保持一些距离
y_lower = 10
#接下来对每一个簇都进行循环
for i in range(n_clusters):
#在获得的每个样本的轮廓系数中抽取出属于第i簇的轮廓系数,并且需要进行排序
#因为排序之后的图像看着就像是递增或递减,更能直观的观察
#sample_silhouette_values是轮廓系数,clusterer_labels是每个样本的分簇,clusterer_labels == i就是取出第i簇的轮廓系数
ith_cluster_silhouette_values = sample_silhouette_values[clusterer_labels == i]
#会改掉原数据的顺序
ith_cluster_silhouette_values.sort()
#这个簇的样本数是多少
size_cluster_i = ith_cluster_silhouette_values.shape[0]
#这个簇在y轴上面的取值,应该从y_lower开始作为最小值,从初始加上这个簇中样本的数量为结束值
y_upper = y_lower + size_cluster_i
#在colormap库中,使用小数来调用颜色
#在nipy_spectral([输入任意小数来代表一个颜色])
#在这里希望的是每个簇的颜色是不同的,需要的颜色种类就是分簇的个数
#使用这个可以确保不同的簇有不同的颜色,只要小数是确定的,颜色就不会改变
#不一定是这种除法,只要保证是小数,而且相同簇的小数是相同的即可
color = cm.nipy_spectral(float(i)/n_clusters)
#开始填充子图1中的内容
#fill_between 是让一个范围中的柱状图都显示统一颜色的函数
#fill_betweenx 的范围是在纵坐标上
#fill_betweeny 的范围是在横坐标上
#fill_betweenx 的参数应该输入(纵坐标的下限,纵坐标的上限,对应横坐标的取值,柱状图的颜色)
ax1.fill_betweenx(np.arange(y_lower,y_upper)
,ith_cluster_silhouette_values
,facecolor=color
,alpha=0.7)
#为每一个簇的轮廓系数写上编号,并且让编号显示在坐标轴的每个条形图中间的位置
#text的参数为(要显示编号的位置的横坐标,要显示编号的位置的纵坐标,要显示的编号内容)
ax1.text(-0.05 #为了不在0的位置显示,所以在-0.05,这样就可以空出来了
,y_lower + 0.5*size_cluster_i #取得一个簇的样本数的中间值作为编号的存放位置
,str(i))
#为下一个簇计算新的y轴上面的初始值,是每一次迭代之后,y的上限在加上10
#以此来保证,下一次的簇不会覆盖上一次的簇并且不同簇之间是有空隙的
#这里的价10是因为在最上面设置的y的初始值为10,就代表每个空隙都要是10
y_lower = y_upper + 10
#对子图1设置标题,x轴的名字,y轴的名字
ax1.set_title("The silhouette plot for the various clusters.")
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
#将总样本的平均轮廓系数用虚线在子图里画出来,方便进行比对
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
#设置y轴不显示刻度
ax1.set_yticks([])
#设置x轴的取值范围
ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
#对第二个子图进行处理,首先获取颜色,这里的颜色要和上面画子图一时候每个簇对应的颜色相同,这就是使用colormap的原因
#所以颜色对应的小数的计算方法要和画子图1的时候要相同
#所以使用最开始得到的聚类结果转为float来进行计算
colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
#画散点图,和上面的《第一次聚类》中一样
ax2.scatter(X[:,0],X[:,1]
,marker='o'
,s=8
,c=colors)
#获得每个簇中的质心
centers = clusterer.cluster_centers_
#将质心添加到散点图里
ax2.scatter(centers[:, 0], centers[:, 1], marker='x',
c="red", alpha=1, s=200)
#对子图2设置标题
ax2.set_title("The visualization of the clustered data.")
ax2.set_xlabel("Feature space for the 1st feature")
ax2.set_ylabel("Feature space for the 2nd feature")
#设置fig的总标题
fig.suptitle(("Silhouette analysis for KMeans clustering on sample data"
"with n_clusters = %d" % n_clusters),
fontsize=14, fontweight='bold'#使用粗体
)
plt.show()
7. 根据上图总结
- 可以看到分2簇的时候,绿色的分的很好,但是黑色的拉低了均值,轮廓系数是0.7,对于分析来说这样分也不是不可以,主要是看具体要求
- 当分三簇的时候,可以看见黑色的没有超过平均轮廓系数的,而且还有一些轮廓系数是小于0的,所以这种分法不好
- 当分4簇的时候,效果还是很好的,每个簇都对平均轮廓系数做出了贡献
- 当分5簇的时候,发现有两个分簇拉低了平均轮廓系数,并且有小于0的轮廓系数
- 当分的簇越来越多的时候,做出贡献越来越小的分簇也就越来越多,甚至有轮廓系数小于0的,证明这些分法很不好
进行筛选之后可以看出,当分为2簇或分为4簇的时候,效果还是很不错的,可以根据实际情况来进行相应的选择
2.2 重要参数init & random_state & n_init:初始质心怎么放好?
在K-Means中有一个重要的环节,就是放置初始质心。如果有足够的时间,K-means一定会收敛,但Inertia可能收敛到局部最小值。是否能够收敛到真正的最小值很大程度上取决于质心的初始化。init就是用来帮助我们决定初始化方式的参数。
初始质心放置的位置不同,聚类的结果很可能也会不一样,一个好的质心选择可以让K-Means避免更多的计算,让算法收敛稳定且更快。在之前讲解初始质心的放置时,我们是使用”随机“的方法在样本点中抽取k个样本作为初始质心,这种方法显然不符合”稳定且更快“的需求。为此,我们可以使用random_state参数来控制每次生成的初始质心都在相同位置,甚至可以画学习曲线来确定最优的random_state是哪个整数(不经常用)。
一个random_state对应一个质心随机初始化的随机数种子。如果不指定随机数种子,则sklearn中的K-means并不会只选择一个随机模式扔出结果,而会在每个随机数种子下运行多次,并使用结果最好的一个随机数种子来作为初始质心。我们可以使用参数n_init来选择,每个随机数种子下运行的次数。这个参数不常用到,默认10次,如果我们希望运行的结果更加精确,那我们可以增加这个参数n_init的值来增加每个随机数种子下运行的次数。
为了优化选择初始质心的方法,2007年Arthur, David, and Sergei Vassilvitskii三人他们开发了”k-means ++“初始化方案,使得初始质心(通常)彼此远离,以此来引导出比随机初始化更可靠的结果。
在sklearn中,我们使用参数init ='k-means ++'来选择使用k-means ++作为质心初始化的方案。通常来说,建议保留默认的"k-means++"的方法。
- init:可输入"k-means++","random"或者一个n维数组。这是初始化质心的方法,默认"k-means++"。输入"k-means++":一种为K均值聚类选择初始聚类中心的聪明的办法,以加速收敛。如果输入了n维数组,数组的形状应该是(n_clusters,n_features)并给出初始质心。
- random_state:控制每次质心随机初始化的随机数种子
- n_init:整数,默认10,使用不同的质心随机初始化的种子来运行k-means算法的次数。最终结果会是基于Inertia来计算的n_init次连续运行后的最佳输出
plus = KMeans(n_clusters = 10).fit(X)
#迭代次数
plus.n_iter_
>7
random = KMeans(n_clusters = 10,init="random",random_state=420).fit(X)
#迭代次数
random.n_iter_
>19
可以看出,在使用默认的init=‘k-means++’要比random迭代次数要少,这个是随机的,也有可能十分接近,但是不会比random大。
不过k-means++要比random的运行时间要长,初步猜测是计算要复杂,如果要详细理解看源码
2.3 重要参数max_iter & tol:让迭代停下来
在之前描述K-Means的基本流程时我们提到过,当质心不再移动,Kmeans算法就会停下来。但在完全收敛之前,我们也可以使用max_iter,最大迭代次数,或者tol,两次迭代间Inertia下降的量,这两个参数来让迭代提前停下来。有时候,当我们的n_clusters选择不符合数据的自然分布,或者我们为了业务需求,必须要填入与数据的自然分布不合的n_clusters,提前让迭代停下来反而能够提升模型的表现。
- max_iter:整数,默认300,单次运行的k-means算法的最大迭代次数
- tol:浮点数,默认1e-4,两次迭代间Inertia下降的量,如果两次迭代之间Inertia下降的值小于tol所设定的值,迭代就会停下
random = KMeans(n_clusters = 10,init="random",max_iter=10,random_state=420).fit(X)
y_pred_max10 = random.labels_
silhouette_score(X,y_pred_max10)
>0.3952586444034157
random = KMeans(n_clusters = 10,init="random",max_iter=20,random_state=420).fit(X)
y_pred_max20 = random.labels_
silhouette_score(X,y_pred_max20)
>0.3401504537571701
可以看见设置max_iter等于10的表现要好于等于20的,在这里就是为了了解这个参数所以才让n_clusters = 10
2.4 重要属性与重要接口
2.5 函数cluster.k_means
sklearn.cluster.k_means (X, n_clusters, sample_weight=None, init=’k-means++’, precompute_distances=’auto’,n_init=10, max_iter=300, verbose=False, tol=0.0001, random_state=None, copy_x=True, n_jobs=None,algorithm=’auto’, return_n_iter=False)
函数k_means的用法其实和类非常相似,不过函数是输入一系列值,而直接返回结果。一次性地,函数k_means会依次返回质心,每个样本对应的簇的标签,inertia以及最佳迭代次数。
from sklearn.cluster import k_means
#输入特征矩阵,需要分的簇的个数,return_n_iter默认为False,调整为True可以返回最大迭代次数
k_means(X,4,return_n_iter=True)
总结
KMeans是最简单的聚类算法,但是其代码比较多,需要耐心进行一点点的了解
对于KMeans的参数,属性,接口列表请看KMeans参数属性接口列表