机器学习笔记(十二):TensorFlow实战四(图像识别与卷积神经网络)
1 - 卷积神经网络常用结构
1.1 - 卷积层
我们先来介绍卷积层的结构以及其前向传播的算法。
一个卷积层模块,包含以下几个子模块:
- 使用0扩充边界(padding)
- 卷积窗口过滤器(filter)
- 前向卷积
- 反向卷积(可选)
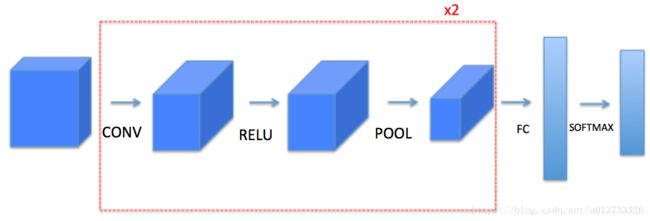
1.1.2 - 边界填充
边界填充将会在图像边界周围添加值为0的像素点,如下图所示:
使用0填充边界有以下好处:
-
卷积了上一层之后的CONV层,没有缩小高度和宽度,这对建立更深的网络非常重要,否则在更深层时,高度/宽度会缩小。一个重要的例子是“same”卷积,自重高度/宽度在卷积完一层之后会被完全保留。
-
它可以帮助我们在图像边界保留更多信息,在没有填充的情况下,卷积过程中图像边缘的极少数值会受到过滤器的影响从而导致信息丢失。
1.1.3 - 卷积窗口过滤器
在这里,我们要实现第一步卷积,我们要使用一个过滤器来卷积输入的数据。先来看看下面这个gif :
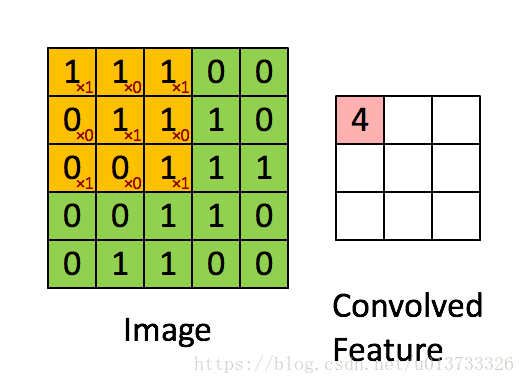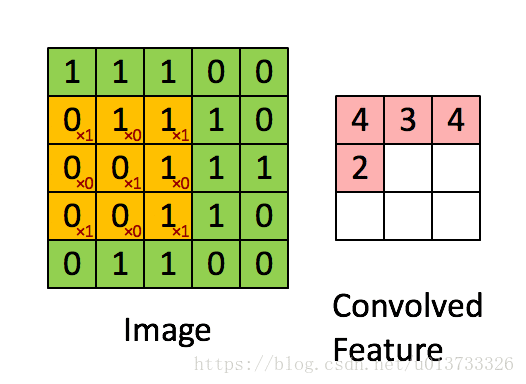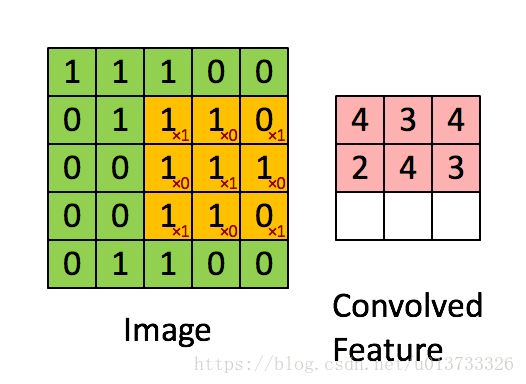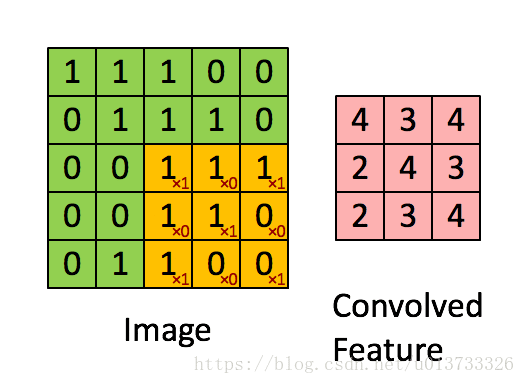
在目前比较成熟的卷积神经网络中,一般过滤器使用3X3或者5X5的矩阵
1.3.4 - 卷积神经网络 - 前向传播
在前向传播的过程中,我们将使用多种过滤器对输入的数据进行卷积操作,每个过滤器会产生一个2D的矩阵,我们可以把它们堆叠起来,于是这些2D的卷积矩阵就变成了高维的矩阵。
我们需要实现一个函数以实现对激活值进行卷积,我们需要在激活值矩阵 A p r e v A_{prev} Aprev上使用过滤器 W W W进行卷积,该函数的输入时前一层的激活输出 A p r e v A_{prev} Aprev, F F F个过滤器,其权重矩阵为 W W W、偏置矩阵为 b b b,每个过滤器只有一个偏置,最后,我们需要一个包含了步长 s s s和填充 p p p的字典的超参数。
小提示:
-
如果我要在矩阵A_prev(shape = (5,5,3))的左上角选择一个2x2的矩阵进行切片操作,那么可以这样做:
a_slice_prev = a_prev[0:2,0:2,:] -
如果我想要自定义切片,我们可以这么做:先定义要切片的位置,vert_start、vert_end、horiz_start、horiz_end,它们的位置我们看一下下面的图就明白了。

我们还是说一下输出维度的计算公式吧:
n H = ⌊ n H p r e v − f + 2 × p a d s t r i d e ⌋ + 1 n_H = \left \lfloor \frac{n_{Hprev}-f+2\times pad}{stride} \right \rfloor+1 nH=⌊stridenHprev−f+2×pad⌋+1
n W = ⌊ n W p r e v − f + 2 × p a d s t r i d e ⌋ + 1 n_W = \left \lfloor \frac{n_{Wprev}-f+2\times pad}{stride} \right \rfloor+1 nW=⌊stridenWprev−f+2×pad⌋+1
n C = 过 滤 器 数 量 n_C=过滤器数量 nC=过滤器数量
1.2 - 卷积层的TenforFlow实现
TensorFlow对卷积神经网络提供了非常好的支持,下面的程序实现了一个卷积层的前向传播过程。
#通过tf.get_variable的方式创建过滤器的权重变量和偏置项变量。
#因为卷积层的参数值和过滤器的尺寸、深度以及当前层节点矩阵的深度有关,所以这里声明的参数变量
#是一个四维矩阵,前面两个维度代表了过滤器的尺寸,第三个维度表示当前层的深度,第四个维度表示过滤器的深度
filter_weight = tf.get_variable(
'weights', [5,5,3,16],
initializer=tf.truncated_normal_initializer(stddev=0.1))
#和卷积层的权重类似,当前层矩阵上不同位置的偏置项也是共享的,所以总共有一下层深度个不同的偏置项。
#本例代码中16位过滤器的深度,也是神经网络中下一层节点矩阵的深度。
biases = tf.get_variable(
'biases',[16],initializer=tf.constant_initializer(0.1))
#tf.nn.conv2d 提供了一个非常方便的函数来实现卷积层前向传播的算法,这个函数的第一个输入为当前层的节点矩阵
#注意这个矩阵是一个四维矩阵,后面三个维度对应一个节点矩阵,第一维对应一个输入batch.比如在输入层,input[0,:,:,:]
#表示第一张图片,input[1,:,:,:]表示第二张图片,以此类推。tf.nn.conv2d第二个参数提供了卷积层的权重,第三个参数为
#不同维度上的步长,虽然第三个参数提供的是一个长度为4的数组,但是第一维和最后一维数字要求一定是1,这是因为卷积层
#的步长只对矩阵的长和宽有效,最后一个参数是填充(padding)的方法,TensorFlow中提供SAME或者VALID两种选择。其中SAME
#表示全添加0填充,“VALID”表示不添加
conv = tf.nn.conv2d(
input,filter_weight,strides=[1,1,1,1],padding='SAME')
#tf.nn.bias_add提供了一个方便的函数给每一个节点加上偏置项。注意这里不能直接使用加法,因为矩阵上不同位置上的节点都需要
#加上同样的偏置项。
bias = tf.nn.bias_add(conv,biases)
#将计算结果通过Relu激活函数完成去线性化
actived_conv = tf.nn.relu(bias)
1.2 - 池化层
池化层会减少输入的宽度和高度,这样它会较少计算量的同时也使特征检测器对其输入中的位置更加稳定
-
最大值池化层:在输入矩阵中滑动一个大小为 f x f_x fx的窗口,选取窗口里的值中的最大值,然后作为输出的一部分。
-
均值池化层:在输入矩阵中滑动一个大小为 f x f_x fx的窗口,计算窗口里的值中的平均值,然后这个均值作为输出的一部分

池化层没有用于反向传播的参数,但是它们有像窗口的大小为f的超参数,它制定fxf窗口的高度和宽度,我们可以计算出最大值或平均值。
1.4.1 - 池化层的前向传播
现在我们要在同一个函数中实现最大值池化层和均值池化层(最大值池化层应用的更多),和之前计算输出维度一样,池化层的计算也是一样的。
n H = ⌊ n H p r e v − f s t r i d e ⌋ + 1 n_H = \left \lfloor \frac{n_{Hprev}-f}{stride} \right \rfloor+1 nH=⌊stridenHprev−f⌋+1
n W = ⌊ n W p r e v − f s t r i d e ⌋ + 1 n_W = \left \lfloor \frac{n_{Wprev}-f}{stride} \right \rfloor+1 nW=⌊stridenWprev−f⌋+1
n C = n C p r e v n_C=n_{Cprev} nC=nCprev
1.3 - 池化层的TensorFlow实现
#tf.nn.max_pool实现了最大池化层的前向传播过程,它的参数和tf.nn.conv2d函数类似。
#ksize提供了过滤器的尺寸,strides提供了步长信息,padding提供了是否使用全0填充
pool = tf.nn.max_pool(
actived_conv,ksize=[1,3,3,1],strides=[1,2,2,1],padding='SAME')
对比池化层和卷积层前向传播在TensorFlow中的实现,可以发现函数的参数形式是相似的。在tf.nn.max_pool函数中,首先需要传入当前层的节点矩阵,这个矩阵是一个四维矩阵,格式和tf.nn.conv2d函数中的第一个参数一致,第二个参数为过滤器的尺寸,虽然给出的是一个长度为4的一维数组,但是这个数组的第一个和最后一个数必须为1.这意味着池化层的过滤器是不可以跨不同输入样例或者节点矩阵深度的。
在实际应用中使用得最多的池化层过滤器尺寸为【1,2,2,1】或者【1,3,3,1】