数学建模十大算法02—插值与拟合（拉格朗日插值、三次样条插值、线性最小二乘法……）

引入

插值： 求过已知有限个数据点的近似函数。（强调这个近似函数要过所有已知点）
拟合： 已知有限个数据点，求近似函数，可不过已知数据点，只要求在某种意义下它在这些点上的总偏差最小。
插值和拟合都是要根据一组数据构造一个函数作为近似，由于近似的要求不同，二者的数学方法上是完全不同的。 而面对一个实际问题，究竟应该用插值还是拟合，有时容易确定，有时则并不明显。

一、插值

在工程和数学应用中，经常有这样一类数据处理问题，在平面上给定一组离散点列，要求一条曲线，把这些点按次序连接起来，称为插值。

我们为什么要进行插值呢？
我们进行数据处理的理想，当然是希望数据非常的完备，啥玩意儿都有。但现实往往不尽如人意，数据经常会缺东少西的，那怎么办呢？

我们需要对一些不存在的数据进行一些插补。比如，我们分析某个餐馆在一段时间内的营收情况，但某一天收银系统出问题了，这天都是手工收款入账的，我们的系统里面就没有这一天的营收数据。那怎么办呢？我们就需要根据一定的办法把这天的营收数据给找补回来，那怎么找补呢？常用的方法有：

已知 $n+1$ 个点 $\left(x_i,y_i\right)$ $(i=0,1,...,n)$，下面求各种插值函数。

1.1 分段线性插值

简单地说，将每两个相邻的节点用直线连起来，如此形成的一条折线就是分段线性插值函数。计算$x$点的插值时，只用到$x$左右的两个节点，计算量与节点个数$n$无关。但$n$越大，分段越多，插值误差越小。
假设两个节点为$\left(x_1,y_1\right)\left(x_2,y_2\right)$，则该区间上的一次线性方程为：

其证明过程非常简单：


以上就是分段线性插值的原理，可以看出原理十分简单。分段线性插值运算量较小，插值误差较小，插值函数具有连续性，但是由于在已知点的斜率是不变的，所以导致插值结果不光滑，存在角点。

该方法可用matlab自带的interp1函数实现。

x = 0:10;  % 已知x值
y = x.*sin(x);  % 已知y值（表达式）
x1 = 0:0.25:10;   % 要求的插值点
y1 = interp1(x,y,x1);  % 用一维插值方法求出的值，默认method为linear
plot(x,y,'k*',x1,y1)

其运行的结果如下所示：

实际上用函数表作插值计算时，分段线性插值就足够了，如数学、物理中用的特殊函数表，数理统计中用的概率分布表等。

1.2 牛顿插值法

首先我们要知道牛顿多项式的形式：${\mathrm{N}}_{\mathrm{n}}(\mathrm{x})={\mathrm{a}}_0+{\mathrm{a}}_1\left(\mathrm{x}-{\mathrm{x}}_0\right)+{\mathrm{a}}_2\left(\mathrm{x}-{\mathrm{x}}_0\right)\left(\mathrm{x}-{\mathrm{x}}_1\right)+\cdots +{\mathrm{a}}_{\mathrm{n}}\left(\mathrm{x}-{\mathrm{x}}_0\right)\left(\mathrm{x}-{\mathrm{x}}_1\right)\cdots \left(\mathrm{x}-{\mathrm{x}}_{\mathrm{n}-1}\right)$
其中$a_k(k=0,1,...,n)$为待定系数。

自变量之差与因变量之差之比叫差商。

定义: 函数 $\mathrm{y}=\mathrm{f}(\mathrm{x})$ 在区间 $\left[{\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{i}+1}\right]$ 上的平均变化率
$$\mathrm{f}\left[{\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{i}+1}\right]=\frac{\mathrm{f}\left({\mathrm{x}}_{\mathrm{i}+1}\right)-\mathrm{f}\left({\mathrm{x}}_{\mathrm{i}}\right)}{{\mathrm{x}}_{\mathrm{i}+1}-{\mathrm{x}}_{\mathrm{i}}}$$
称为 $f(x)$ 关于 $x_i,x_{i+1}$ 的一阶差商，并记为 $f\left[x_i,x_{i+1}\right]$

二阶差商：
$$\mathrm{f}\left[{\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{i}+1},{\mathrm{x}}_{\mathrm{i}+2}\right]=\frac{\mathrm{f}\left[{\mathrm{x}}_{\mathrm{i}+1},{\mathrm{x}}_{\mathrm{i}+2}\right]-\mathrm{f}\left[{\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{i}+1}\right]}{{\mathrm{x}}_{\mathrm{i}+2}-{\mathrm{x}}_{\mathrm{i}}}$$
$\mathrm{m}$ 阶差商：
$$\mathrm{f}\left[{\mathrm{x}}_0,{\mathrm{x}}_1,\cdots ,{\mathrm{x}}_{\mathrm{m}}\right]=\frac{\mathrm{f}\left[{\mathrm{x}}_1,{\mathrm{x}}_2,\cdots ,{\mathrm{x}}_{\mathrm{m}}\right]-\mathrm{f}\left[{\mathrm{x}}_0,{\mathrm{x}}_1,\cdots ,{\mathrm{x}}_{\mathrm{m}-1}\right]}{{\mathrm{x}}_{\mathrm{m}}-{\mathrm{x}}_0}$$

那么，牛顿插值公式为：

更多细节请参考：数值分析（一） 牛顿插值法及matlab代码

1.3 拉格朗日插值多项式

举个简单的例子，比如说，已知下面这几个点，我想找一根穿过它们的曲线：

我们可以合理的假设，这根曲线是一个二次多项式：

这是因为有三个已知的点，可以通过下列方程组解出这个二次多项式：

不过这里不打算通过解方程来得到这根二次曲线，如果已知的点有很多，那我们需要解的方程组会很复杂，因此我们来看看拉格朗日是怎么巧妙解出这根曲线的？

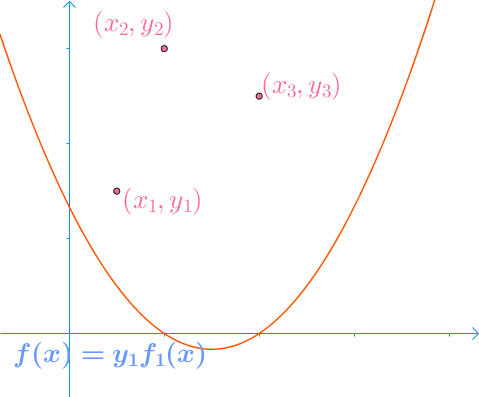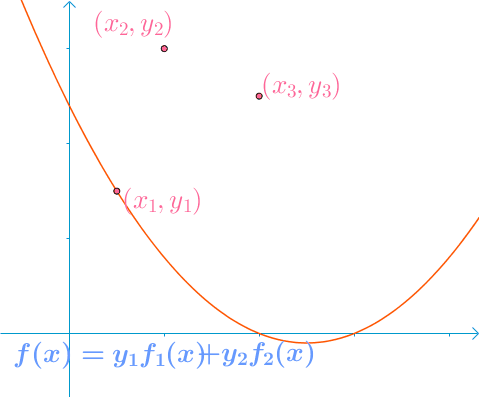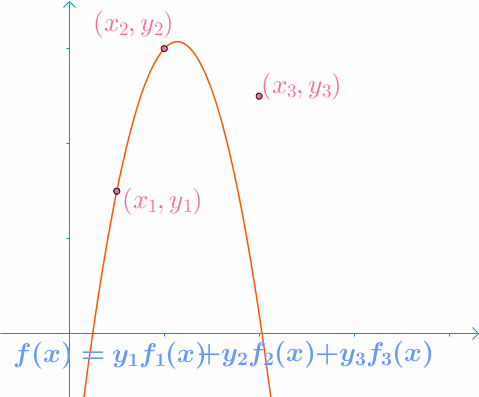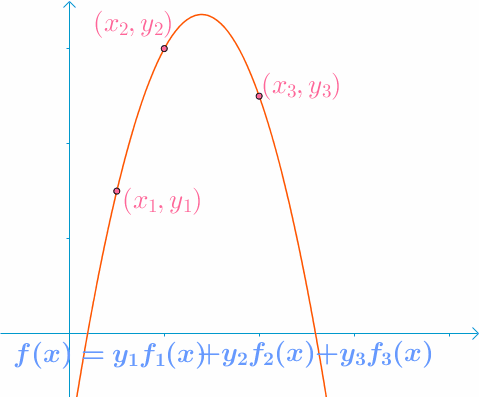
首先，第一根曲线$f_1(x)$，在 $x_1$ 点处，取值为1，其余两点取值为0：

第二根曲线$f_2(x)$，在 $x_2$ 点处，取值为1，其余两点取值为0：

第三根曲线$f_3(x)$，在 $x_3$ 点处，取值为1，其余两点取值为0：

这三根曲线就是拉格朗日需要的，我们来看看为什么？

那么 $f(x)=y_1{f}_1(x)+y_2{f}_2(x)+y_3{f}_3(x)$ 这个方程就可以经过已知的三个点。

就可以穿过这三个点，用一个动图直观理解下：

最终得到的曲线就是拉格朗日找到的曲线：

用严格的数学表达来理解拉格朗日插值法，过程如下：

拉格朗日（Lagrange）插值的基函数为：$$\begin{array}{rl}{l}_i(x)& =\frac{\left(x-x_0\right)\cdots \left(x-x_{i-1}\right)\left(x-x_{i+1}\right)\cdots \left(x-x_n\right)}{\left(x_i-x_0\right)\cdots \left(x_i-x_{i-1}\right)\left(x_i-x_{i+1}\right)\cdots \left(x_i-x_n\right)}\\ & =\prod _{\begin{array}{c}j=0\\ j\ne i\end{array}}^n\frac{x-x_j}{x_i-x_j},i=0,1,\cdots ,n_{\circ }\end{array}$$
$l_i(x)$是$n$次多项式，满足
$$l_i\left(x_j\right)=\{\begin{array}{l}0,j\ne i\\ 1,j=i_{\circ }\end{array}$$
拉格朗日插值函数为：
$$L_n(x)=\sum _{i=0}^n{y}_i{l}_i(x)=\sum _{i=0}^n{y}_i\left(\prod _{\begin{array}{c}j=0\\ j\ne i\end{array}}^n\frac{x-x_j}{x_i-x_j}\right)$$
我们可以将给定的 $n+1$ 个点带入拉格朗日基本多项式（插值基函数），发现当且仅当 $i=j$ 时取1，其余情况取0，这样就保证了$L$ 经过这$n+1$ 个点。

matlab代码如下：

function y0=Lagrange(x,y,x0)
n=length(x);
l=ones(1,n);
y0=0;
for j=1:n
    for k=1:n
        if j~=k  % j≠k时
           l(j)=l(j)*(x0-x(k))/(x(j)-x(k));
        end
    end
end
for i=1:n
    y0=y0+l(i)*y(i);
end

1.4 样条插值

许多工程技术中提出的计算问题对插值函数的光滑性有较高要求，如飞机的机翼外形，内燃机的进、排气门的凸轮曲线，都要求曲线具有较高的光滑程度，不仅要连续，而且要有连续的曲率，这就导致了样条插值的产生。

样条（Spline） 本来是工程设计中使用的一种绘图工具，是富有弹性的细木条或细金属条。绘图员利用它把一些已知点连接成一条光滑曲线（称为样条曲线），并使连接点处有连续的曲率。三次样条插值就是由此抽象而来的。

简单来说，样条插值就是根据每两个相邻的数据点确定一段函数，然后再结合成一个函数，那么就是光滑的函数了。

数学上将具有一定光滑性的分段多项式称为样条函数。具体地说，给定区间[a,b]的一个分划：

如果函数 $S(x)$ 满足：

1.4.1 三次样条插值

利用样条函数进行插值，即取插值函数为样条函数，称为样条插值。例如分段线性插值是一次样条插值。这里只介绍三次样条插值，即已知函数 $y=f(x)$ 在区间 $[a,b]$ 上的 $n+1$ 个节点 $a=x_0<x_1<\cdots <x_{n-1}<x_n=b$ 上的值 $y_i=f(x_i)(i=0,\mathrm{1...},n)$ ，求插值函数 $S(x)$ ，使得：


Matlab中三次样条插值有如下函数：

y = interp1(xdata,ydata,x,'spline');
y = spline(xdata,ydata,x);
pp = csape(x0,y0,conds); y = fnval(pp,x);
pp = csape(x0,y0,conds,valconds); y = fnval(pp,x);

pp = csape(x0,y0)使用默认的边界条件，即Lagrange边界条件。

pp = csape(x0,y0,conds,valconds)中的conds的指定插值的边界条件，其值可为：

• ‘complete’ 边界为一阶导数，一阶导数的值在valconds参数中给出，若忽略valconds参数视为默认情况。
• 'second’边界为二阶导数，二阶导数的值在参数valconds中给出，不使用参数valconds，默认值为[0,0]。
  

1.5 二维插值

前面讲述的都是一维插值，即节点为一维变量，插值函数是一元函数(曲线)。若节点是二维的，插值函数就是二元函数，即曲面。 如在某区域测量了若干点（节点）的高程（节点值），为了画出较精确的等高线图，就要先插入更多的点（插值点），计算这些点的高程（插值）。

1.5.1 插值节点为网格节点

Matlab中计算二维插值的命令如下：

z = interp2(x0,y0,z0,x,y,'method')

其中：$x_0$, $y_0$ 分别为 $m$ 维和 $n$ 维向量，表示节点；$z_0$为 $n\times m$ 矩阵，表示节点值；$x$, $y$ 为一维数组，表示插值点，$x$与$y$应是方向不同的向量，即一个是行向量，另一个是列向量；$z$为矩阵，它的行数为$y$的维数，列数为$x$的维数，表示得到的插值；'method’的用法同上面的一维插值。

【例】 测得平板表面3×5网格点处的温度分别为：

试作出平板表面温度分布曲面$z=f(x,y)$的图形。

第一步：先在三维坐标画出原始数据，画出粗糙的温度分布曲面。

x=1:5;
y=1:3;
temps=[82 81 80 82 84;79 63 61 65 81;84 84 82 85 86];
mesh(x,y,temps)  % 构建空间曲面图（mesh画的是曲线网格图，surf画的是曲面网格图）

第二步：以平滑数据，在x、y方向上每隔0.2个单位的地方进行插值。

xi=1:0.2:5;
yi=1:0.2:3;
zi=interp2(x,y,temps,xi',yi,'cubic');  % 注意这里x和y形状不一样，任意一个作为行向量，另一个作为列向量
mesh(xi,yi,zi)

用contour(xi,yi,zi,20,'r')作其等高线图（等高线图：z值一样的点连起来的图）如下：

如果是三次样条插值，可以使用命令：

pp = csape({x0,y0},z0,conds,valconds);
z = fnval(pp,{x,y});

其中：$x_0$, $y_0$ 分别为 $m$ 维和 $n$ 维向量；$z_0$为 $m\times n$ 矩阵；$z$为矩阵，它的行数为$x$的维数，列数为$y$的维数，表示得到的插值，具体使用方法同一维插值。

1.5.2 插值节点为散乱节点

注意此时已知的是n个节点，和1.5.1的m×n个节点情况不同。

对上述问题，Matlab中提供了插值函数griddata，其格式为：

ZI = griddata(x,y,z,XI,YI);

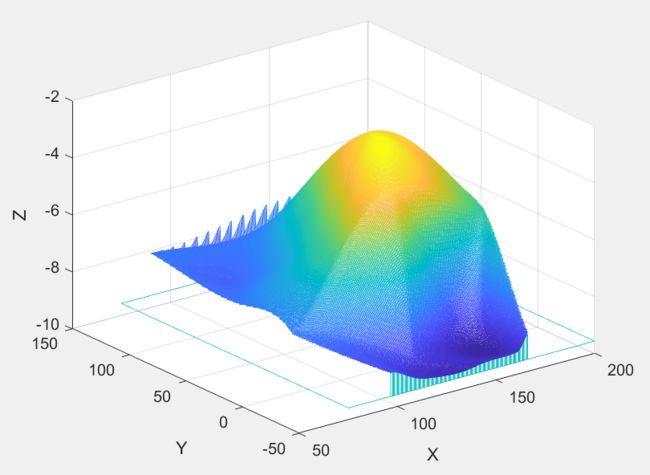
【例】 在某海域测得一些点$(x,y)$处的水深z由下表给出，船的吃水深度为5英尺，在矩形区域 $(75，200)\times (-50，150)$ 里的哪些地方船要避免进入。在矩形区域内画出海底曲面的图形。

由题意得，船的吃水深度小于5米时，船比较容易搁浅。

x=[129 140 103.5 88 185.5 195 105 157.5 107.5 77 81 162 162 117.5];
y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5];
z=[-4 -8 -6 -8 -6 -8 -8 -9 -9 -8 -8 -9 -4 -9];
cx=75:0.5:200;  % 矩形区域
cy=-50:0.5:150;
cz=griddata(x,y,z,cx,cy','cubic');  % 采用立方插值在矩形区域内做二维插值
figure(1),meshz(cx,cy,cz);  % 海底曲线图
xlabel('X'),ylabel('Y'),zlabel('Z');

figure(2),contour(cx,cy,cz,[-5 -5],'r');  % 画出深度为5米的等高线，则在等高线内部的深度均小于5米
grid; 
hold on;
plot(x,y,'+');  % 二维坐标中标出数据各个点位置
xlabel('X'),ylabel('Y');

红色曲线内部的点都是船比较容易搁浅的位置。

1.6 例题

【例】机床加工。 待加工零件的外形根据工艺要求由一组数据 $(x,y)$ 给出（在平面情况下），用程控铣床加工时每一刀只能沿 $x$ 方向和 $y$ 方向走非常小的一步，这就需要从已知数据得到加工所要求的步长很小的 $(x,y)$ 坐标。
表5.1中给出的 $x,y$ 数据位于机翼断面的下轮廓线上，假设需要得到 $x$ 坐标每改变0.1时的 $y$ 坐标。试完成加工所需数据，画出曲线，要求用最近项插值、分段线性插值和三次样条插值（不同边界）方法计算。

Matlab代码如下：

x0=[0 3 5 7 9 11 12 13 14 15];
y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];
x=0:0.1:15;
% ------最近项插值
y1 = interp1(x0,y0,x,'nearest');
subplot(1,5,1)
plot(x0,y0,'+',x,y1);
title('nearest method');
% ------ 线性插值
y2 = interp1(x0,y0,x); 
subplot(1,5,2)
plot(x0,y0,'+',x,y2);
title('Piecewise linear');
% ------立方样条插值
y3 = interp1(x0,y0,x,'spline');
subplot(1,5,3)
plot(x0,y0,'+',x,y3)
title('Splinel')
% ------三次样条插值的Lagrange边界条件
pp1 = csape(x0,y0);
y4 = fnval(pp1,x);
subplot(1,5,4)
plot(x0,y0,'+',x,y4)
title('Spline2')
% ------指定插值边界条件为二阶导数
pp2 = csape(x0,y0,'second');
y5 = fnval(pp2,x);  % 使用fnval函数求插值点的函数值
subplot(1,5,5)
plot(x0,y0,'+',x,y5);
title('Spline3')

其运行结果为：

我们可以明显感觉到，三次样条插值得到的曲线会更加平滑。

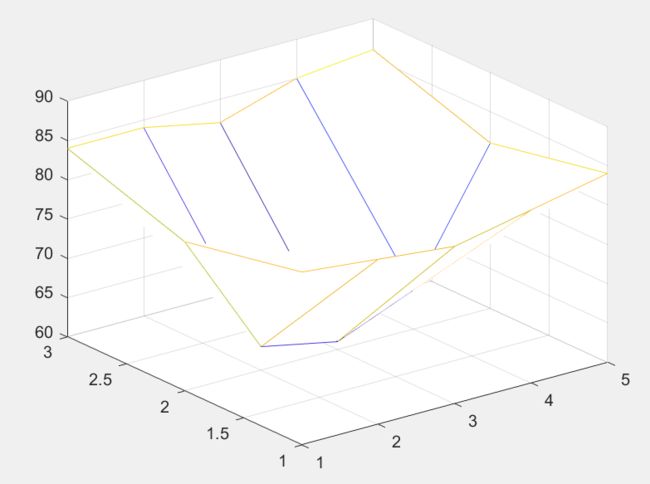
【例】 在某山区测得一些地点的高程如下表。平面区域为 $1200\le x\le 4000,1200\le y<3600$，试用Matlab中的最邻近插值、双线性插值和双三次插值3种方法作出该山区的地貌图和等高线图，并求出最高和最低点，并对几种插值方法进行比较。

首先，第一步我们做出已知点的网格面。

x=1200:400:4000;
y=1200:400:3600;
[xx,yy]=meshgrid(x,y);  % xx是以x为行（列数为向量x的长度）的矩阵，yy是以y为列（行数为y的长度）的矩阵。[xx,yy]矩阵x和矩阵y合在一起
z=[1130 1250 1280 1230 1040 900 500 700; 1320 1450 1420 1400 1300 700 900 850; 
    1390 1500 1500 1400 900 1100 1060 950; 1500 1200 1100 1350 1450 1200 1150 1010;
    1500 1200 1100 1550 1600 1550 1380 1070; 1500 1550 1600 1550 1600 1600 1600 1550; 
    1480 1500 1550 1510 1430 1300 1200 980];
figure(1);
meshz(x,y,z)
xlabel('X'),ylabel('Y'),zlabel('Z')
title('网格面')

然后，我们用最邻近插值法看一下插值结果：

xi=1200:40:4000;
yi=1200:40:3600;
figure(2)
z1i=interp2(x,y,z,xi,yi','nearest');
subplot(1,2,1),surfc(xi,yi,z1i),xlabel('X'),ylabel('Y'),zlabel('Z'),title('最邻近插值');
subplot(1,2,2),contour(xi,yi,z1i,10,'r'),title('最邻近插值等高线图');

同样，看一下线性插值法及其等高线图。

figure(3)
z2i=interp2(x,y,z,xi,yi','linear');
subplot(1,2,1),surfc(xi,yi,z2i),xlabel('X'),ylabel('Y'),zlabel('Z'),title('线性插值');
subplot(1,2,2),contour(xi,yi,z2i,10,'r'),title('线性插值等高线图');

立方插值法及其等高线图：

figure(4)
z3i=interp2(x,y,z,xi,yi','cubic');
subplot(1,2,1),surfc(xi,yi,z3i),xlabel('X'),ylabel('Y'),zlabel('Z'),title('立方插值');
subplot(1,2,2),contour(xi,yi,z3i,10,'r'),title('立方插值等高线图');

三次样条插值法及等高线图：

figure(5)
z4i=interp2(x,y,z,xi,yi','spline');
subplot(1,2,1),surfc(xi,yi,z4i),xlabel('X'),ylabel('Y'),zlabel('Z'),title('三次样条插值');
subplot(1,2,2),contour(xi,yi,z4i,10,'r'),title('三次样条插值等高线图');

分段线性插值法及其等高线图：

figure(6)
z5i=interp2(x,y,z,xi,yi');
subplot(1,2,1),surfc(xi,yi,z5i),xlabel('X'),ylabel('Y'),zlabel('Z'),title('分段线性插值');
subplot(1,2,2),contour(xi,yi,z5i,10,'r'),title('分段线性插值等高线图');

比较由以上五种插值方法得到的地貌图和等高线图，可以看出：

• 由于两个高度之间直线为最短距离，因此利用最邻近插值得到的地貌图和等高线为直线，描述的山地地貌皆为陡崖，对于一般山区的地貌是不符合的；
• 分段线性插值得到的图像随着分段数目的增多，而更加平缓，棱角更加不明显。
• 利用线性插值、三次样条插值和立方插值所得到的图像较为平滑，更加适合描述该山地的地貌。

二、拟合

2.1 曲线拟合的线性最小二乘法

原则上不需要经过图像中的任何一个点，只要保证与各点的距离总体足够小即可。

线性最小二乘法是解决曲线拟合最常用的方法，其基本思路是，令

拟合的准则是使 $y_i$ 与 $f(x_i)$ 的距离的平方和最小，称为最小二乘法。

那么，系数$a_k$该怎么确定呢？这里参考了《数学建模算法与应用》的证明过程。
1）系数$a_k$的确定


2）函数$r_k(x)$的选取
面对一组数据 $(x_i,y_i)$, $i=1,2,...,n$，用线性最小二乘法作曲线拟合时，首要的也是关键的一步是恰当地选取 $r_1(x),..,r_m(x)$ 。如果通过机理分析，能够知道y与x之间的函数关系, 则 $r_1(x),..,r_m(x)$ 容易确定。若无法知道 $y$ 与 $x$ 之间的关系，通常可以将数据 $(x_i,y_i)$, $i=1,2,...,n$ 作图，直观地判断应该用什么样的曲线去作拟合。常用的曲线有如下：

已知一组数据，用什么样的曲线拟合最好，可以在直观判断的基础上，选几种曲线分
别拟合，然后比较，看哪条曲线的最小二乘指标 $J$ 最小。

在Matlab中，线性最小二乘法的标准型为：

【例】 用最小二乘法求一个形如 $y=a+b{x}^2$ 的经验公式，拟合下表中的数据。

X=[19 25 31 38 44]';
Y=[19.0 32.3 49.0 73.3 97.8]';
R=[ones(5,1),x.^2]

我们看一下这里R的值，进一步理解上文推导过程中的含义：

用Matlab标准型的命令求系数：

ab=R\Y

求得的结果如下：

意味着，求得的拟合公式为：$y=0.9726+0.05x^2$。

我们来看一下该曲线的拟合效果如何？

x0=19:0.1:44;
y0=ab(1)+ab(2)*x0.^2;
plot(X,Y,'o',x0,y0,'r')

注：这里可以联想到GM(1,1)模型中用到了最小二乘法。

2.2 多项式拟合

如果取

即用 $m$ 次多项式拟合给定数据，MatLab中有现成的函数a=polyfit(x0,y0,m)。
其中，输入参数$x_0、y_0$ 为要拟合的数据； $m$ 为拟合多项式的次数。输出参数 $a$ 为拟合多项式的系数向量。

【例】 某乡镇企业1990年—1996年的生产利润如表所列。

试预测1997年和1998年的利润。

思路如下：
首先第一步我们可以作已知数据的散点图，直观判断其需要什么样的多项式拟合。

x0=[1990  1991  1992  1993  1994  1995  1996];
y0=[70   122   144   152   174   196   202];
plot(x0,y0,'*')

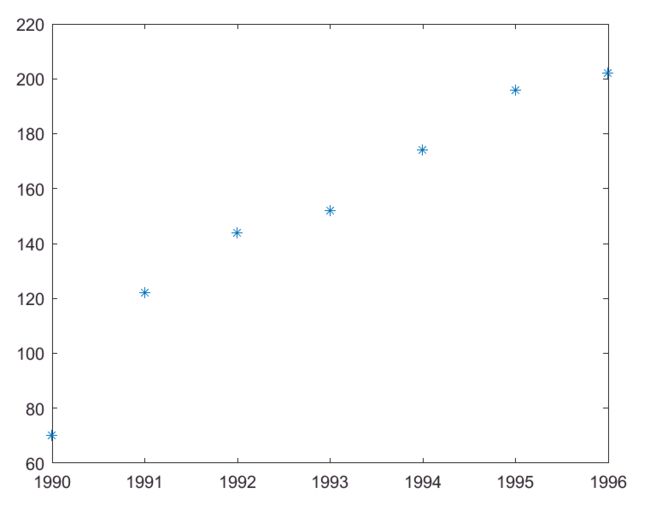
我们可以发现，该乡镇企业的年生产利润几乎直线上升。因此，可以用 $y=a_{1}x+a_0$ 作为拟合函数来预测该乡镇企业未来的年利润。代码如下：

x0=[1990  1991  1992  1993  1994  1995  1996];
y0=[70   122   144   152   174   196   202];
a=polyfit(x0,y0,1)
y97=polyval(a,1997)
y98=polyval(a,1998)

最终求得的结果为：（注意，次数高的项在前面）

2.3 指定函数拟合

fittype是自定义拟合函数，cfun=fit(x,y,f)。拟合数据 $x、y$ 必须为列向量。

假设原始数据散点图如下所示：

我们可以编写一个m文件来实现自定义拟合函数。

 syms t
 x = [0;0.4;1.2;2;2.8;3.6;4.4;5.2;6;7.2;8;9.2;10.4;11.6;12.4;13.6;14.4;15];
 y = [1;0.85;0.29;-0.27;-0.53;-0.4;-0.12;0.17;0.28;0.15;-0.03;-0.15;-0.071;0.059;0.08;0.032;-0.015;-0.02];
 f = fittype('a*cos(k*t)*exp(w*t)','independent','t','coefficients',{'a','k','w'});
 cfun = fit(x,y,f)    %显示拟合函数
 xi = 0:.1:20;
 yi = cfun(xi);
 plot(x,y,'r*',xi,yi,'b-');

求出来系数 $a、k、w$ 的值分别为：

三、综合案例

先挖一个坑在这，有空再来写。

参考文章

[1] 插值算法——分段线性插值（1）
[2] 如何直观地理解拉格朗日插值法？（知乎）
[3] 数值分析（一） 牛顿插值法及matlab代码
[4] 数值分析（二) 三次样条插值法matlab程序
[5] 数学建模学习-插值法
[6] 数学建模——拟合