PSO算法求解整数规划问题举例

2020-4-30粒子群算法已更新，有需要的同学移步“PSO算法求解（上）-基本PSO”和“PSO算法求解（下）-罚函数方法”，欢迎留言交流以及指正错误！

前言：最近在使用群智能算法求解线性规划问题的过程中，由于初次设计该方面的知识，在网络上检索了许多相关的智能算法的案例进行学习。首先选择了粒子群算法求解线性规划问题，但是网络上已有的一些资料对于非专业出身的同学来说理解较为困难，并且没有专门解决线性规划的实例，因此在这里进行一次分享。注意：代码可能啰嗦，适用于初入同学，有错误请指正。

首先，简要介绍一下粒子群算法。
粒子群算法（PSO）是一种起源于鸟群觅食行为的智能算法，其基本思想是通过整个群体中的个体之间的合作来寻找最优解。在粒子群算法中，粒子具有速度和位置两种属性，分别表示在搜索空间中表示搜索的快慢和搜索的方向。在搜索过程中，粒子在搜索空间中单独的进行搜寻，获得粒子个体的最优适应值（pbest），然后和群体当中的其他粒子进行合作比较，所有粒子的个体最优适应值中的最大值最为当前搜索过程中的全局最适应值(gbest)，并根据当前的个体最优适应值和全局最适应值来调整粒子自身的速度和位置，直至搜索过程结束。在搜索过程中，粒子更新速度和位置的式子如下：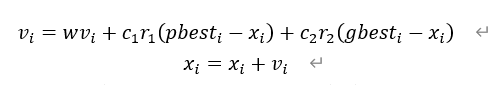
其中，c_1和c_2是学习因子；r_1和r_2是0和1之间的随机数；w是惯性权重。粒子群算法工作流程如下：

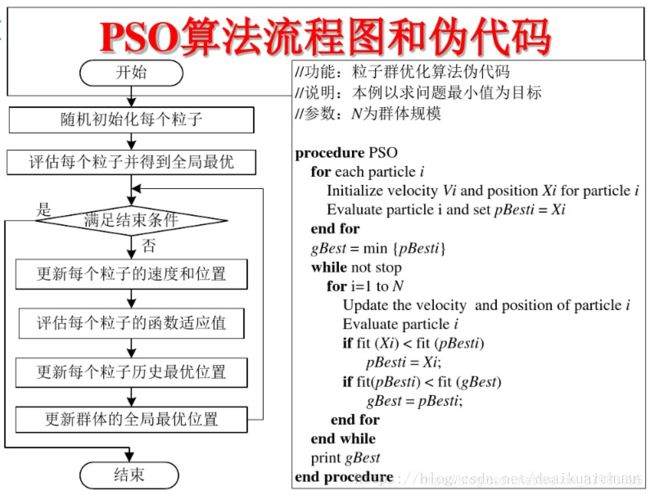
图片来源于图片来源，具体内容请转至链接处进行了解

求解线性规划案例如下：
max z=6x1+2x2+3x3+5x4
4x1+2x2+x3+3x4<=10
3x1-5x2+x3+6x4>=4
2x1+x2+x3-x4<=3
x1+2x2+4x3+5x4<=10
x1,x2,x3,x4=0 or 1

普通粒子群算法求解代码：

#include
#include   
#include
#include
#include 
#include
#include 
#include 

using namespace std;

//测试1：整数规划0-1
//max z=6x1+2x2+3x3+5x4
//	4x1+2x2+x3+3x4<=10
//	3x1-5x2+x3+6x4>=4
//	2x1+x2+x3-x4<=3
//	x1+2x2+4x3+5x4<=10
//	x[j]=0 or 1
//最优解z=14,x=(1,0,1,1)

//测试2：整数规划0 - 1
//max z=20x1+40x2+20x3+30X4
//	5x1+4x2+3x3+8x4<=18
//	x1+7x2+9x3+6x4<=22
//	8x1+10x2+2x3+10x4<=24
//	x[j]=0 or 1
//最优解z=90,x=(0,1,1,1)

//PSO参数
const int person_number = 20;//种群个体数目
const int dimension = 4;//搜索空间维度->变量数
double weight;//惯性权重
double LDW_ini = 0.9;//线性递减权值策略（LDW）
double LDW_end = 0.4;
double c1=2, c2=2;//学习因子
const int maxgen = 50;//迭代次数

double X_pos[person_number][dimension];//粒子位置变量
double V_speed[person_number][dimension];//粒子速度变量
double pbest[person_number];//粒子适应值
double max_pbest;//临时个体最优值
double gbest;//粒子最优值
double gbest_temp;//临时全局最优值--->更新历史值时使用
double gbest_temp_2;//临时全局最优值--->约束判断中使用
int gbest_index=0;//迭代过程中全局最优时的粒子位置
int gbest_X[dimension] = { 0 };//记录相应的X取值

//数据记录
double iter_arr[maxgen];//记录迭代次数
double gbest_arr[maxgen];//记录迭代过程中的最优值

//目标约束
const int const_num = 4;//约束数量
double C[dimension] = { 6,2,3,5 };
double A[const_num][dimension] = { {4,2,1,3},{3,-5,1,6},{2,1,1,-1},{1,2,4,5} };
double B[const_num] = { 10,4,3,10 };
//const int const_num = 3;//约束数量
//double C[dimension] = { 20,40,20,30 };
//double A[const_num][dimension] = { {5,4,3,8},{1,7,9,6},{8,10,2,10} };
//double B[const_num] = { 18,22,24 };

//目标函数
double Fitness(int pers, int dim) {//输入参数->粒子数，维数
	double fit = 0;
	for (int j = 0; j < dim; j++) {
		fit = fit + C[j] * X_pos[pers][j];
	}
	return fit;
}

//约束条件
double Constraint(int dim,int index ) {//维数，max_pbest所在粒子位置
	float constraint[const_num] = { 0 };
	gbest_temp_2 = 0;
	for (int i = 0; i < const_num; i++) {
		for (int j = 0; j < dim; j++) {
			constraint[i] = constraint[i] + A[i][j] * X_pos[index][j];
		}
	}
	if (constraint[0] <= B[0] && constraint[1] >= B[1] && constraint[2] <= B[2] && constraint[3] <= B[3]) {
	//if (constraint[0] <= B[0] && constraint[1] <= B[1] && constraint[2] <= B[2]) {
		if (max_pbest > gbest_temp_2) {//更新历史最优值
			gbest_temp_2 = max_pbest;
		}
		else {
			gbest_temp_2 = gbest_temp_2;
		}
	}
	return gbest_temp_2;
}

//权重设置
double Weight(int ITER) {
	double pso_weight = 0;
	//惯性权重
	//weight = 0.8;
	//权重计算-2
	pso_weight = ((LDW_ini - LDW_end)*(maxgen - ITER) / maxgen) + LDW_end;
	return pso_weight;
}

//初始化
void initial() {	
	for (int i = 0; i < person_number;i++) {
		for (int j = 0; j < dimension; j++) {
			X_pos[i][j] = (double)(rand() % 2);//0or1
			//V_speed[i][j] = rand() % 2;//0or1
			V_speed[i][j] = rand() % (9 + 1) / (float)(9 + 1);//0-1
		}
	}
	//初始化个体极值
	for (int i = 0; i < person_number; i++) {
		pbest[i] = Fitness(i,dimension);
	}
	//初始化全局极值---->判断是否满足约束，否则gbest=0;
	max_pbest = 0;
	for (int i = 0; i < person_number; i++) {
		if (pbest[i] > max_pbest) {
			max_pbest = pbest[i];
			gbest_index = i;
		}
		else {
			max_pbest = max_pbest;
			gbest_index = gbest_index;
		}
	}
	gbest = Constraint(dimension, gbest_index);
}

void pso() {
	int iter = 0;
	srand(time(NULL));
	while (iter<maxgen) {
		//惯性权重
		 //weight = 0.8;
		//权重计算
		weight=Weight(iter);

		//更新速度和位置
		for (int i = 0; i < person_number;i++) {
			for (int j = 0; j < dimension;j++) {
				float r_rand[2];
				for (int k = 0; k < 2;k++) {
					r_rand[k]= rand() % (9 + 1) / (float)(9 + 1);
				}
				V_speed[i][j] = weight * V_speed[i][j] + c1 * r_rand[0]*(pbest[i]-X_pos[i][j]) + c2 * r_rand[0] * (gbest - X_pos[i][j]);	
				if (V_speed[i][j] < 0 || V_speed[i][j] > 1)V_speed[i][j] = rand() % (9 + 1) / (float)(9 + 1);

				X_pos[i][j] = X_pos[i][j] + V_speed[i][j];
				if (X_pos[i][j] !=0 || X_pos[i][j] != 1)X_pos[i][j] = (double)(rand() % 2); 

			}	
		}
		
		//更新个体最优值
		for (int i = 0; i < person_number; i++) {	
			pbest[i] = Fitness(i,dimension);
		}
		
		max_pbest = 0;//临时个体最优值
		for (int i = 0; i < person_number; i++) {
			if (pbest[i] > max_pbest) {
				max_pbest = pbest[i];
				gbest_index= i;
			}
			else {
				max_pbest = max_pbest;
				gbest_index = gbest_index;
			}
		}

		//约束条件判断
		gbest_temp = Constraint(dimension, gbest_index);

		//更新历史最优值
		if (gbest_temp > gbest) {
			gbest = gbest_temp;
			for (int j = 0; j < dimension; j++) {
				gbest_X[j] = X_pos[gbest_index][j];
			}
		}
		else {
			gbest = gbest;
			for (int j = 0; j < dimension; j++) {
				gbest_X[j] = gbest_X[j];
			}
		}
		iter_arr[iter] = iter;
		gbest_arr[iter] = gbest;
		iter++;
	}
}

int main() {
	initial();
	pso();
	pso_out();
	cout << "gbest=" << gbest << endl;
	cout << "X" << endl;
	for (int j = 0; j < dimension; j++) {
		cout << gbest_X[j] << " "; 
		}
	system("pause");
	return 0;
}

自适应权重粒子群算法求解代码：

#include
#include   
#include
#include
#include 
#include
#include 
#include 

using namespace std;

//测试1：整数规划0-1
//max z=6x1+2x2+3x3+5x4
//	4x1+2x2+x3+3x4<=10
//	3x1-5x2+x3+6x4>=4
//	2x1+x2+x3-x4<=3
//	x1+2x2+4x3+5x4<=10
//	x[j]=0 or 1
//最优解z=14,x=(1,0,1,1)

//测试2：整数规划0 - 1
//max z=20x1+40x2+20x3+30X4
//	5x1+4x2+3x3+8x4<=18
//	x1+7x2+9x3+6x4<=22
//	8x1+10x2+2x3+10x4<=24
//	x[j]=0 or 1
//最优解z=90,x=(0,1,1,1)

//PSO参数
const int person_number = 20;//种群个体数目
const int dimension = 4;//搜索空间维度->变量数
double weight;//惯性权重
double LDW_ini = 0.9;//线性递减权值策略（LDW）
double LDW_end = 0.4;
double c1=2, c2=2;//学习因子
const int maxgen = 50;//迭代次数

double X_pos[person_number][dimension];//粒子位置变量
double V_speed[person_number][dimension];//粒子速度变量
double pbest[person_number];//粒子适应值
double max_pbest;//临时个体最优值
double gbest;//粒子最优值
double gbest_temp;//临时全局最优值--->更新历史值时使用
double gbest_temp_2;//临时全局最优值--->约束判断中使用
int gbest_index=0;//迭代过程中全局最优时的粒子位置
int gbest_X[dimension] = { 0 };//记录相应的X取值

//数据记录
double iter_arr[maxgen];//记录迭代次数
double gbest_arr[maxgen];//记录迭代过程中的最优值

//目标约束
const int const_num = 4;//约束数量
double C[dimension] = { 6,2,3,5 };
double A[const_num][dimension] = { {4,2,1,3},{3,-5,1,6},{2,1,1,-1},{1,2,4,5} };
double B[const_num] = { 10,4,3,10 };
//const int const_num = 3;//约束数量
//double C[dimension] = { 20,40,20,30 };
//double A[const_num][dimension] = { {5,4,3,8},{1,7,9,6},{8,10,2,10} };
//double B[const_num] = { 18,22,24 };

//目标函数
double Fitness(int pers, int dim) {//输入参数->粒子数，维数
	double fit = 0;
	for (int j = 0; j < dim; j++) {
		fit = fit + C[j] * X_pos[pers][j];
	}
	return fit;
}

//约束条件
double Constraint(int dim,int index ) {//维数，max_pbest所在粒子位置
	float constraint[const_num] = { 0 };
	gbest_temp_2 = 0;
	for (int i = 0; i < const_num; i++) {
		for (int j = 0; j < dim; j++) {
			constraint[i] = constraint[i] + A[i][j] * X_pos[index][j];
		}
	}
	if (constraint[0] <= B[0] && constraint[1] >= B[1] && constraint[2] <= B[2] && constraint[3] <= B[3]) {
	//if (constraint[0] <= B[0] && constraint[1] <= B[1] && constraint[2] <= B[2]) {
		if (max_pbest > gbest_temp_2) {//更新历史最优值
			gbest_temp_2 = max_pbest;
		}
		else {
			gbest_temp_2 = gbest_temp_2;
		}
	}
	return gbest_temp_2;
}

//权重设置
double Weight(int ITER) {
	double pso_weight = 0;
	//权重计算
	pso_weight = ((LDW_ini - LDW_end)*(maxgen - ITER) / maxgen) + LDW_end;
	return pso_weight;
}

//初始化
void initial() {	
	for (int i = 0; i < person_number;i++) {
		for (int j = 0; j < dimension; j++) {
			X_pos[i][j] = (double)(rand() % 2);//0or1
			//V_speed[i][j] = rand() % 2;//0or1
			V_speed[i][j] = rand() % (9 + 1) / (float)(9 + 1);//0-1
		}
	}
	//初始化个体极值
	for (int i = 0; i < person_number; i++) {
		pbest[i] = Fitness(i,dimension);
	}
	//初始化全局极值---->判断是否满足约束，否则gbest=0;
	max_pbest = 0;
	for (int i = 0; i < person_number; i++) {
		if (pbest[i] > max_pbest) {
			max_pbest = pbest[i];
			gbest_index = i;
		}
		else {
			max_pbest = max_pbest;
			gbest_index = gbest_index;
		}
	}
	gbest = Constraint(dimension, gbest_index);
}

void pso() {
	int iter = 0;
	srand(time(NULL));
	while (iter<maxgen) {
		//权重计算
		weight=Weight(iter);

		//更新速度和位置
		for (int i = 0; i < person_number;i++) {
			for (int j = 0; j < dimension;j++) {
				float r_rand[2];
				for (int k = 0; k < 2;k++) {
					r_rand[k]= rand() % (9 + 1) / (float)(9 + 1);
				}
				V_speed[i][j] = weight * V_speed[i][j] + c1 * r_rand[0]*(pbest[i]-X_pos[i][j]) + c2 * r_rand[0] * (gbest - X_pos[i][j]);	
				if (V_speed[i][j] < 0 || V_speed[i][j] > 1)V_speed[i][j] = rand() % (9 + 1) / (float)(9 + 1);

				X_pos[i][j] = X_pos[i][j] + V_speed[i][j];
				if (X_pos[i][j] !=0 || X_pos[i][j] != 1)X_pos[i][j] = (double)(rand() % 2); 

			}	
		}
		
		//更新个体最优值
		for (int i = 0; i < person_number; i++) {	
			pbest[i] = Fitness(i,dimension);
		}
		
		max_pbest = 0;//临时个体最优值
		for (int i = 0; i < person_number; i++) {
			if (pbest[i] > max_pbest) {
				max_pbest = pbest[i];
				gbest_index= i;
			}
			else {
				max_pbest = max_pbest;
				gbest_index = gbest_index;
			}
		}

		//约束条件判断
		gbest_temp = Constraint(dimension, gbest_index);

		//更新历史最优值
		if (gbest_temp > gbest) {
			gbest = gbest_temp;
			for (int j = 0; j < dimension; j++) {
				gbest_X[j] = X_pos[gbest_index][j];
			}
		}
		else {
			gbest = gbest;
			for (int j = 0; j < dimension; j++) {
				gbest_X[j] = gbest_X[j];
			}
		}
		iter_arr[iter] = iter;
		gbest_arr[iter] = gbest;
		iter++;
	}
}

int main() {
	initial();
	pso();
	pso_out();
	cout << "gbest=" << gbest << endl;
	cout << "X" << endl;
	for (int j = 0; j < dimension; j++) {
		cout << gbest_X[j] << " "; 
		}
	system("pause");
	return 0;
}