基于圆内接三角形的快速高精圆检测
一. 背景
从图像中检测识别或者定位圆形几何基元在计算机视觉和机器人领域有着非常广泛的应用。传统的圆检测算法多数是基于Hough Transform (HT), 如OpenCV内嵌的圆检测。但是,现实测试发现OpenCV提供的算法较难满足实际需求, 精度也不够高。 本文介绍的圆检测算法不同于HT采用投票的机制 (依赖离散的像素),而是基于连续圆弧段。相较于HT, 此算法精度更高,检测速度也更快。这篇工作发表在 Pattern Recognition (PR) 上的:An occlusion-resistant circle detector using inscribed triangles . 如果大家需要进行图像中的圆检测,可以试一试。GitHub地址:代码链接
二. 算法流程
算法包括三个主要模块:弧段提取->圆检测->圆验证,如下图1所示
1. 弧段提取
和HT以及RANSAC不同在于,他俩是基于对离散的像素采样投票,而本文方法是提取连续的弧段。为提取弧段,首先提取边缘,这里采用EDPF[^1]算法而不是Canny算子提取边缘。因为EDPF算法不需要手动调节参数,而Canny还要设置高低阈值。如图2所示, (a)是输入的待检测图像,(b)是经过EDPF提取的边缘。
 图2. 弧段提取流程
图2. 弧段提取流程
然后利用以直代曲的思想,用直线段来逼近提取的边缘,目的是为提取弧段。采用 Ramer-Douglas-Peucker (RDP) 算法[^2],结果如图2 ( c ) 所示。根据直线段,我们利用向量内积和外积来判断大角和拐点。这里基于的假设是:属于同一个圆的弧段应该光滑地变化,不应该存在尖锐角和极端的曲率变化。数学表达为:
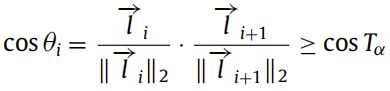
注意这里应该是小于等于符号(论文中自己写反了)
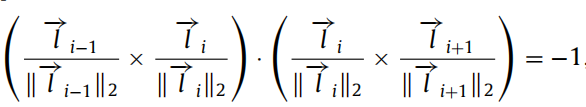
其中 l → \overrightarrow {l} l是所逼近直线段的向量形式。将边缘在大角和拐点处断开就可以得到连续的弧段了,如图2(d)所示。
2. 圆检测
前面的操作都可以视为预处理步,下面要进入圆检测的正题了。在图像圆(基元)检测这个小领域,真正显功夫或能创新的地方就是下面要描述的内容。
2.1 圆弧段组合
为了将属于同一个圆的弧段组合在一起,我在论文中尝试考虑了全局和局部的几何特征。全局特征是凸性,即属于同一个圆的弧段需要形成凸包,怎么用数学式子来表达呢?可以利用弦方程。如图3所示,
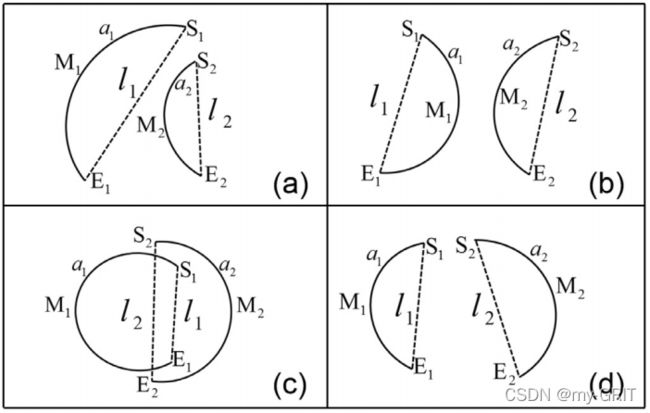 图3. 两弧段相对位置判断
图3. 两弧段相对位置判断
2.1.1 相对位置约束
假设要匹配的两弧段为 a i a_i ai 和 a j a_j aj。首先利用弧段两端点 S i S_i Si 和 E i E_i Ei 定义弦 l i l_i li 所在直线方程
![]()
那么当弧段中点 M i M_i Mi 和另外弧段 a j a_j aj 的两端点 S j S_j Sj 和 E j E_j Ej 同时位于弦 l i l_i li 两侧,且,弧段中点 M j M_j Mj 和另 S i S_i Si 和 E i E_i Ei 同时位于弦 l j l_j lj 两侧时,我们定义两弧段满足相对位置或凸性约束,式子如下:
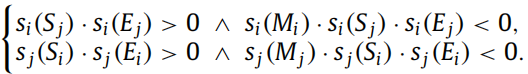
2.1.2 圆内接三角形约束
当两弧段满足全局的相对位置约束之后,我们尝试进一步确定他俩是否真正来自同一圆。为此,利用正弦定理来估算一下这两弧段得到的圆参数,即中心位置和半径。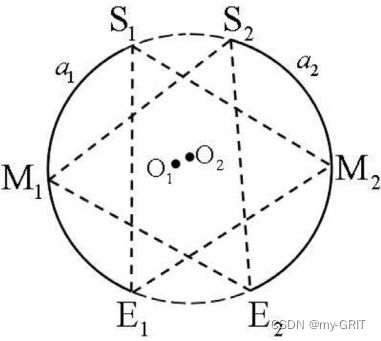
如图4所示,构造两三角形 △ S 1 M 2 E 1 \triangle S_1M_2E_1 △S1M2E1和 △ S 2 M 1 E 2 \triangle S_2M_1E_2 △S2M1E2,根据正弦定理有
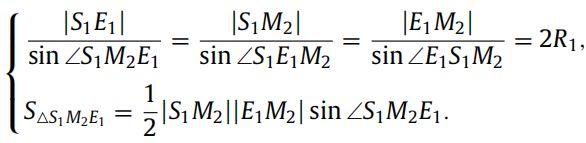
则半径 R R R 和圆心 O O O 可以求出为

值得注意的是,由于我们选择的三角形的三个顶点不共线,因此上式的分母始终不为零。我们可以通过比较估算的两圆参数( R 1 R_1 R1, R 2 R_2 R2)和( O 1 O_1 O1, O 2 O_2 O2),
来确定他们是否真正来自同一圆:
![]()
如果参数确实十分相近,则这两弧段极有可能来自同一圆。为此,我们进一步验证两弧段相对于估计圆的内点率 I R i j IR_{ij} IRij:
![]()
若上式成立,则我们认为这两弧段来自同一圆。
2.1.3 圆参数估计
既然组合的弧段都找到了,通常做法就是利用线性最小二乘进行拟合了。我一开始也想这样做来着,但是后来觉得这样太平凡了,没啥特色,哈哈哈,就琢磨能不能不通过拟合直接估算圆参数,然后就尝试着利用更多的圆内接三角形进行圆参数的估计。
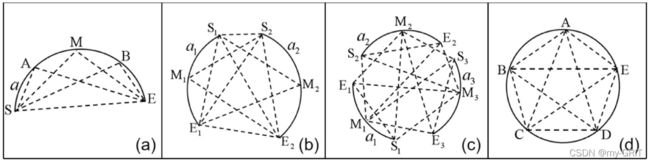
图5. 利用圆内接三角形进行圆参数估计
如图5所示,根据组合的弧段个数将参数估计分成4种情形:
(1) 只有单独一个弧段,构造三个圆内接三角形;
(2) 两个弧段,除了组合时已经构造的俩圆内接三角形,再构造四个圆内接三角形,一共六个;
(3) 对于三个及以上弧段的情形,直接利用组合时构造的所有圆内接三角形;
(4) 对于完整的圆,我们在其上均匀采五个点构造五个圆内接三角形。
然后根据Theil-Sen[^2]估计子,采用所有估计值的中位数作为最终估计的圆参数。图6(b)展示了利用圆内接三角形估计的圆:
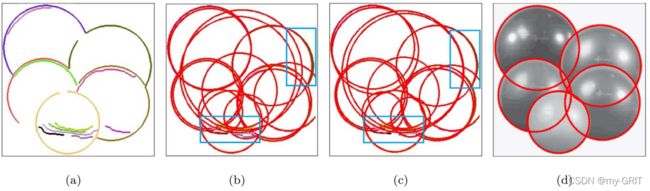
图6. 利用圆内接三角形进行圆参数估计示例
我一开始十分担心估计的参数精度,但当看到效果的时候,也被惊艳到了,还是蛮精确的。为了进一步消除内心的顾虑,再来一步线性误差修正,目的是求出参数估计的偏差。
假定真实的圆参数为 ( R ˉ c , x ˉ c , y ˉ c ) (\bar{R}_c, \bar{x}_c, \bar{y}_c) (Rˉc,xˉc,yˉc)
![]()
估计的参数 ( R ~ , x ~ c , y ~ c ) (\tilde{R}, \tilde{x}_c, \tilde{y}_c) (R~,x~c,y~c) 由于受到噪声的影响,会发生偏差 ( Δ R , Δ x c , Δ y c ) (\Delta{R}, \Delta{x}_c, \Delta{y}_c) (ΔR,Δxc,Δyc), 表示为
![]()
也就是
![]()
如果圆上有 N N N个点,那么
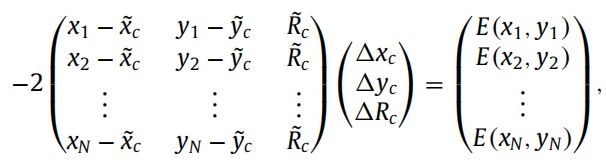
其中
![]() 通过求解如下的线性方程组来得到偏差 ( Δ R , Δ x c , Δ y c ) (\Delta{R}, \Delta{x}_c, \Delta{y}_c) (ΔR,Δxc,Δyc)
通过求解如下的线性方程组来得到偏差 ( Δ R , Δ x c , Δ y c ) (\Delta{R}, \Delta{x}_c, \Delta{y}_c) (ΔR,Δxc,Δyc)
![]()
显示解可以表示为
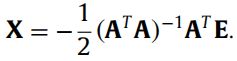
其中 A \bf{A} A是列满秩的系数矩阵。
2.2 圆验证
最后一步我们对检测得到的所有圆进行验证,进一步提升检测精度。这里是同时衡量距离和方向来求内点率:
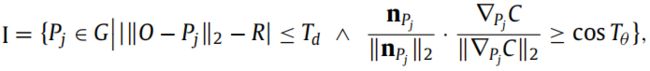
三. 实验验证
论文中是对比了最新的或者经典的五种方法。
3.1 弧段组合验证
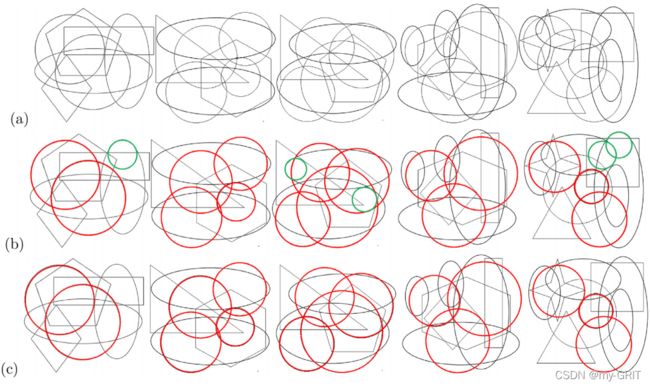
图7. 弧段组合验证示例图。(b)是最新对比方法,©是本文方法,其中红色和绿色分别代表正确检测和错误检测。
3.2 离心率测试
图8. 测试算法随着离心率增大的内点率变化
3.3 噪声边缘的参数估计精度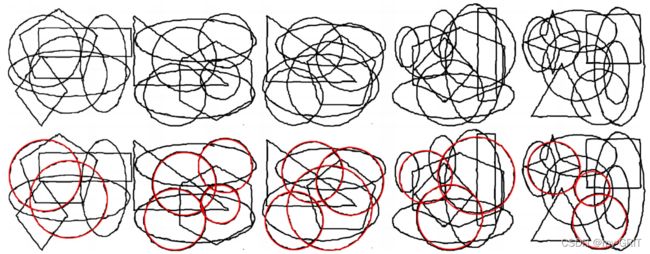
图9. 当边缘受到噪声干扰时,参数估计精度的测试示例。
3.4 超参数敏感度分析
3.5 真实图像数据测试
图 11.真实图像测试示例
3.6 噪声图像测试
四. 总结
论文的主要内容就为大家介绍到这里了,如果大家想了解更多细节,可以阅读论文或留言交流。如果大家有需要,可以试试代码,顺手在Github点个star哈~~
五. 参考文献
[1] C. Akinlar, C. Topal, EDPF: a real-time parameter-free edge segment detector with a false detection control, Int. J. Pattern Recognit. Artif. Intell. 26 (01)(2012) 1255002.
[2] H. Theil, A rank-invariant method of linear and polynomial regression analysis, in: Henri Theil’s Contributions to Economics and Econometrics, 1992, pp. 345–381


