【论文笔记】特征点匹配网络 SuperGlue: Learning Feature Matching with Graph Neural Networks 2019 论文笔记
Magic Leap, ETH Zurich
提出了特征点匹配网络SuperGlue,寻找两幅图像局部特征点之间的对应关系的神经网络,该网络使用图神经网络预测损失。
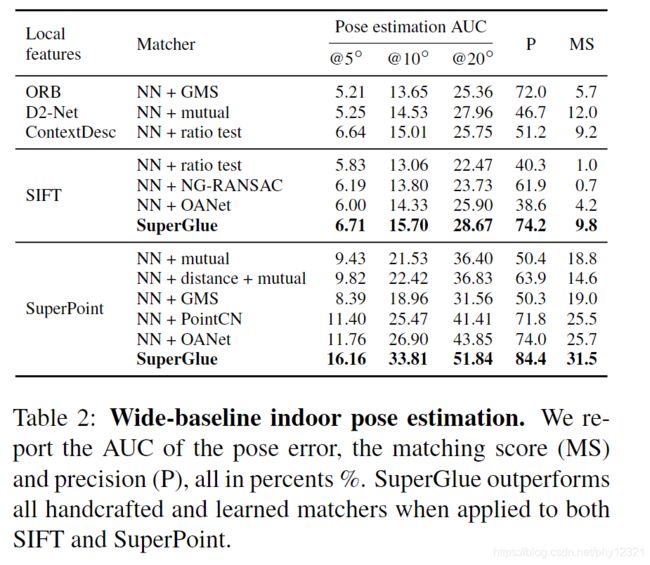
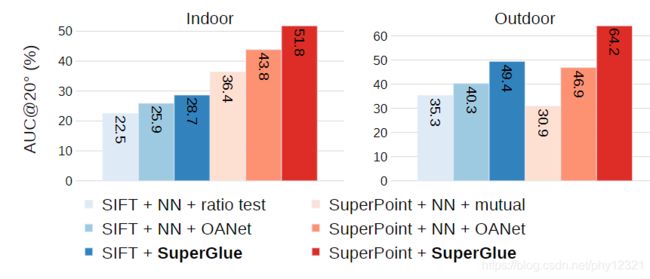
搭配super point在室内外重定位任务中达到SOTA的精度。
论文方法:
首先输入图像对记为A,B,各包含了关键点和局部描述子,因此是集合形式{(p,d)}
p=(x,y,c)是关键点,其中c是置信度;d是描述子,本文中是superpoint。
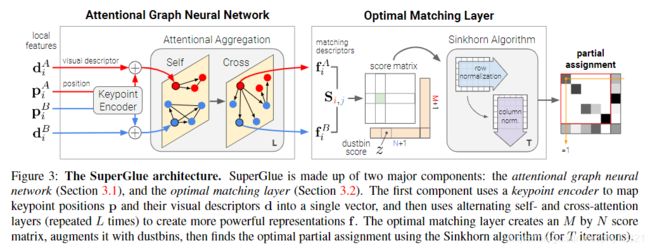
网络结构介绍:
1.图神经网络
借鉴人眼反复匹配的过程:注意力+反复迭代+上下文信息,因此使用注意力图神经网络作为第一个模块,允许图像间、图像间的长距离信息融合。
-
关键点编码:这一步是图神经网络节点 i 的初始化步骤:
( 0 ) x i = d i + M L P e n c ( p i ) ^{(0)}x_i=d_i+MLP_{enc}(p_i) (0)xi=di+MLPenc(pi)
同时编码了位置信息 p和视觉信息d -
该网络为多路复用图神经网络,其节点由两幅图的特征点共同组成。
连接同一图像上两个节点的边为内边,其集合记为 ϵ s e l f \epsilon_{self} ϵself,
连接了来自两个不同图像的特征点的边的集合称为 ϵ c r o s s \epsilon_{cross} ϵcross
迭代更新A中的节点:
( ℓ + 1 ) x i A = ( ℓ ) x i A + M L P ( [ ( ℓ ) x i A ∣ ∣ m ϵ → i ] ) ^{(ℓ+1)}x^A_i=^{(ℓ)}x^A_i+MLP([^{(ℓ)}x^A_i||m_{\epsilon →i}]) (ℓ+1)xiA=(ℓ)xiA+MLP([(ℓ)xiA∣∣mϵ→i])
[…||…]表示将节点i自己的状态和 ϵ \epsilon ϵ集合中的所有指向节点i的边信息级联,然后使用多层感知机B中节点相同。
从 l l l = 1开始,如果是奇数那么$ \epsilon=\epsilon_{self} , 否 则 ,否则 ,否则\epsilon = \epsilon_{cross}$,也就是说在图像内和图像间交叉传播
2.注意力融合
即 状态更新中的 m ϵ → i m_{\epsilon →i} mϵ→i的求解方法:
m ϵ → i = ∑ ( i , j ) ∈ ϵ α i j V j 这 里 使 用 注 意 力 即 加 权 方 法 权 值 α i , j = s o f t m a x ( q i T K j ) , 代 表 q 与 k 之 间 的 相 似 性 度 。 m_{\epsilon →i} = \sum_{(i,j)\in \epsilon}\alpha_{ij}V_j \\这里使用注意力 \ 即加权方法\\权值 \alpha_{i,j} = softmax(q_i^TK_j),代表q与k之间的相似性度。\\ mϵ→i=(i,j)∈ϵ∑αijVj这里使用注意力 即加权方法权值αi,j=softmax(qiTKj),代表q与k之间的相似性度。
其中的q,v,k都是根据每一层迭代结果以及网络层的参数计算出来的:
已知 l l l层迭代的参数为 w 1 , w 2 , w 3 , b 1 , b 2 , b 3 w1,w2,w3,b1,b2,b3 w1,w2,w3,b1,b2,b3,
q i = W 1 ( ℓ ) x i Q + b 1 [ k j v j ] T = [ W 2 W 3 ] T ( ℓ ) x j S + [ b 2 b 3 ] T q_i=W_1^{(ℓ)}x^Q_i+b_1 \\ [k_j\ v_j]^T=[W_2\ W_3]^T \ ^{(ℓ)}x^S_j+[b_2\ b_3]^T qi=W1(ℓ)xiQ+b1[kj vj]T=[W2 W3]T (ℓ)xjS+[b2 b3]T
经过L层的迭代最终的A 中的匹配描述符:
f i A = W ⋅ ( L ) x i A + b , ∀ i ∈ A f^A_i=W·^{(L)}x^A_i+b,\ ∀i∈ A fiA=W⋅(L)xiA+b, ∀i∈A
B中类似。
3.最优匹配层
使用内积定义描述匹配符之间的相似度:
S i , j = < f i A , f j B > , ∀ ( i , j ) ∈ A × B S_{i,j}=
由于肯定会有不匹配的点对,因此新建一个dustbin,专门存放此类特征点
- Sinkhorn Algorithm:使用Sinkhorn 算法对两幅图的特征点进行匹配,该算法是匈牙利算法的可导版本。
4.损失函数
同时最大化精度和召回率:
L o s s = − ∑ ( i , j ) ∈ M l o g P ^ i , j − ∑ i ∈ I l o g P ^ i , N + 1 − ∑ j ∈ J l o g P ^ M + 1 , j Loss=−\sum_{(i,j)\in M}log\hat P_{i,j}−\sum_{i\in I}log\hat P_{i,N+1}−\sum_{j\in J}log\hat P_{M+1,j} Loss=−(i,j)∈M∑logP^i,j−i∈I∑logP^i,N+1−j∈J∑logP^M+1,j
这里的P是局部软匹配矩阵,行列和均为1
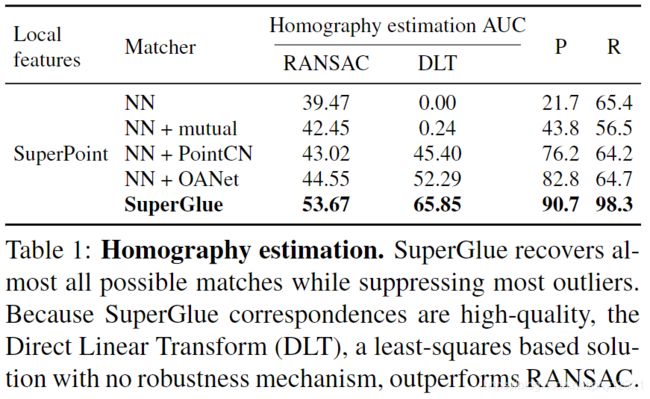
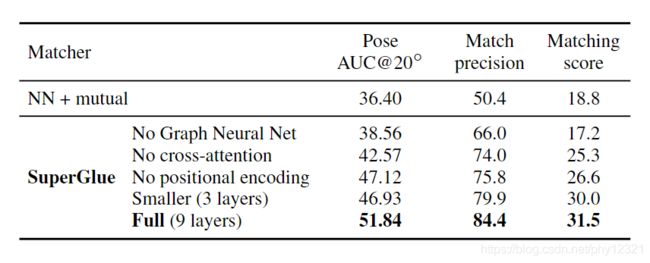
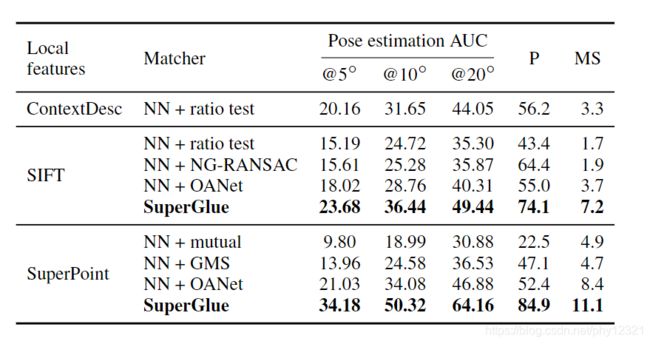
实验评估
速度:GTX1080上15fps