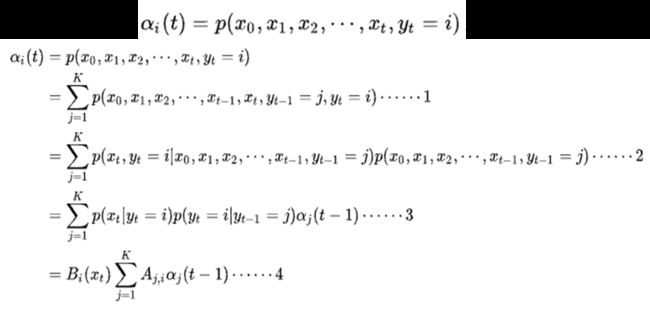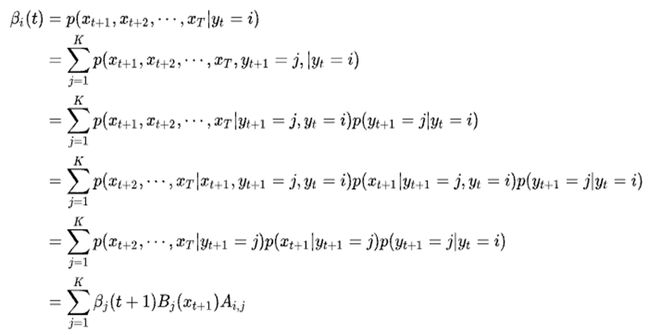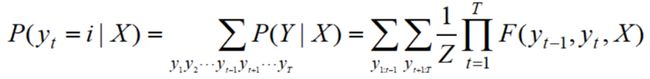HMM、MEMM、CRF
HMM、MEMM、CRF
有问题还请指出,里面参杂了一些个人瞎猜的内容(不猜根本学不下去啊!!),这玩意儿太难了,学这些玩意儿,真的是任重而道远。
很多例子都是引用的b站up主自然卷小蛮和手写AI的内容,非常感谢我查阅到的所有大佬的无私的知识分享!!
朴素贝叶斯
P ( X , y ) = p ( y ) ∑ x ∈ X p ( x ∣ y ) \LARGE P(X, y) = p(y)\sum_{x \in X}p(x|y) P(X,y)=p(y)x∈X∑p(x∣y)
朴素贝叶斯模型解决的是标签为单个值的情况,当标签是一个序列时,就需要HMM。
HMM(隐马尔可夫模型)
建模方式:
两个假设:
-
齐次马尔可夫性假设:当前隐状态仅依赖于前一个隐状态
-
观测独立性假设:观测值之间相互独立,只受当前时间步的隐状态影响
P ( X , Y ) = P ( X ∣ Y ) P ( Y ) = p ( x 1 ∣ y 1 ) p ( y 1 ) ∏ t = 2 T p ( x t ∣ y t ) p ( y t ∣ y t − 1 ) \LARGE P(X, Y) = P(X|\ Y)P(Y)\\ \LARGE= p(x_1|y_1)p(y_1)\prod_{t=2}^{T}p(x_t|\ y_t)p(y_t|\ y_{t-1}) P(X,Y)=P(X∣ Y)P(Y)=p(x1∣y1)p(y1)t=2∏Tp(xt∣ yt)p(yt∣ yt−1)
其中, p ( y t ∣ y t − 1 ) p(y_t|\ y_{t-1}) p(yt∣ yt−1)是转移概率, p ( x t ∣ y t ) p(x_t|\ y_t) p(xt∣ yt)是发射概率, p ( y 1 ) p(y_1) p(y1)是初始概率。
监督学习
例子:中文分词
下面这个例子,来自B站视频。
任务形式:序列标注做中文分词。
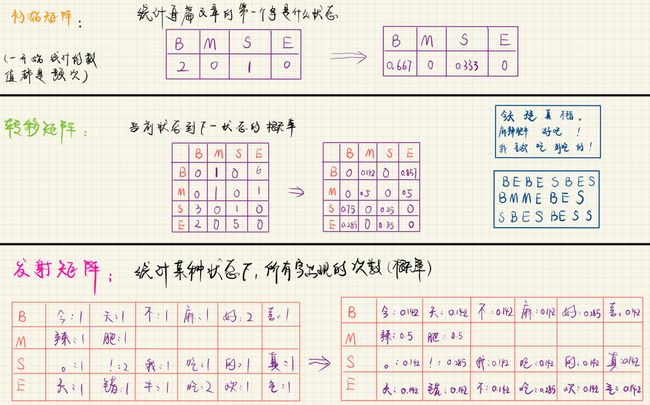
状态空间:Begin、Middle、End、Single。
观测空间:所有出现的文字。
例如:今天/天气/真/不错/。
标签: B E B E S B E S
**训练过程:**统计语料库的内容,得到转移矩阵、发射矩阵、初始矩阵。
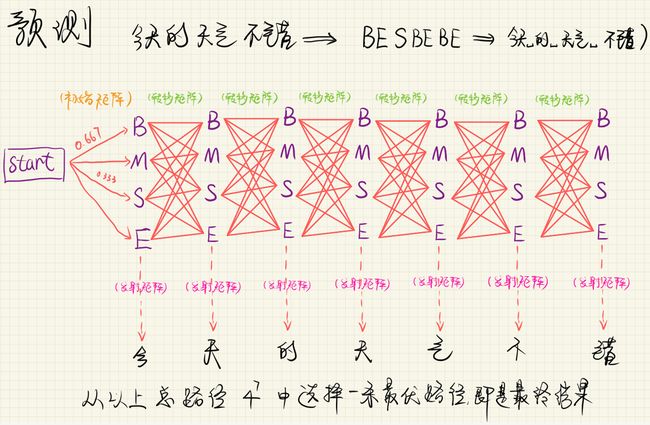
**预测过程:**求出最优路径
问题: 上图共有 4 7 4^7 47条路径,计算量太大
**解决方案:**维特比算法【动态规划】
暂时不考虑发射概率,只考虑转移概率。
初始位置( y 1 y_1 y1)有四种可能,初始概率分别为0.667、0、0.333、0。
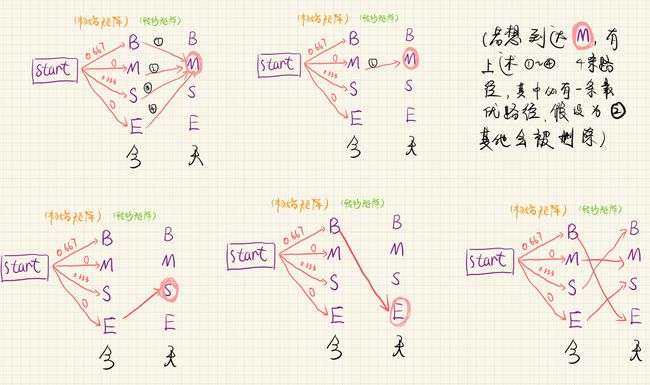
y 2 y_2 y2位置也有四种可能,此时计算(start->B, B->B)、(start->M, M->B)、(start->S, S->B)、(start->E, E->B)的概率,假设(start->B, B->B)的概率值最大(即 y 2 y_2 y2取值为B时,最大概率情况为 y 1 y_1 y1取值为B),则当 y 2 y_2 y2取值为B时,考虑 y i ( i > 2 ) y_i(i>2) yi(i>2)的概率时,不再考虑(start->M, M->B)、(start->S, S->B)、(start->E, E->B)三种情况。
例如这样一句话:今天的天气不错。
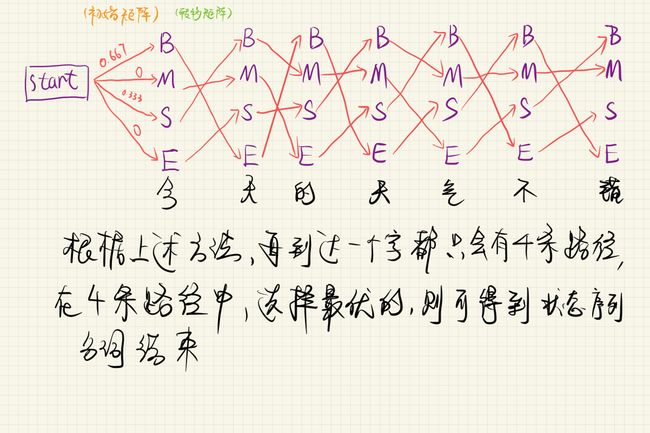
如图,当“天”取状态值“M”时,有①②③④四条路径,假设其中②为最大值,则在推断“气”时,不再将①③④这三条路径考虑为前置路径,即当“天”对应“M”时,“今”只能对应“M”。同理,假设“天”对应“S”时,“今”只能对应“E”。
在神经网络的运用中,发射概率其实就是模型最后得到logits,转移矩阵、初始矩阵是可学习的参数矩阵。
无监督学习
EM算法
例子:词性标注
参考B站视频,以词性标注为例,任务形式为序列标注。
状态值:NN、VB、DT
观测值:所有语料库中出现的单词。
下面是随机初始化的两个矩阵。
P ( X , Y ) = P ( X ∣ Y ) P ( Y ) P ( Y ∣ X ) = P ( X , Y ) / P ( X ) \LARGE P(X, Y) = P(X|\ Y)P(Y)\\ \LARGE P(Y| X) = P(X,Y)/P(X) P(X,Y)=P(X∣ Y)P(Y)P(Y∣X)=P(X,Y)/P(X)
得到两个矩阵后,就能求出 P ( X , Y ) P(X, Y) P(X,Y),但我们所需要的是 P ( Y ∣ X ) P(Y|X) P(Y∣X),通过贝叶斯公式,我们可以通过求 P ( X ) P(X) P(X)推导出 P ( Y ∣ X ) P(Y|X) P(Y∣X)。怎么求 P ( X ) P(X) P(X)呢?
在 P ( X , Y ) P(X,Y) P(X,Y)上对Y进行积分,就能求得 P ( X ) P(X) P(X)
P ( X ) = ∑ Y ′ P ( X , Y ′ ) \LARGE P(X) = \sum_{Y'}P(X,Y') P(X)=Y′∑P(X,Y′)

这里假设只有三种词性,这个长度为3的序列有 3 3 3^3 33种可能,所以要求27项。其中一项的具体计算方式如下:
这27项有很多重复的计算,可以通过前向算法或后向算法简化计算。
前向算法
定义 α i ( t ) α_i(t) αi(t)为到t时刻的部分观测序列为 x 1 , x 2 , … , x t x_1,x_2,…,x_t x1,x2,…,xt,且隐状态为i的概率:
从图中可以看出,只要我知道前一时刻的 α \alpha α值,只需乘上两个矩阵就能得到当前时刻的 α \alpha α值,这与上面公式推导相符。
后向算法
定义 β i ( t ) β_i(t) βi(t)为在t时刻状态为i的条件下,从t+1到T的部分观测序列为 x t + 1 , x t + 2 , … , x T x_{t+1},x_{t+2},…,x_T xt+1,xt+2,…,xT的概率:
通过后向算法,也可以直接求解 P ( X ) P(X) P(X)。
边缘概率
Y ^ = a r g m a x P ( Y ∣ X ) = a r g m a x P ( X , Y ) P ( X ) = a r g m a x P ( X , Y ) \LARGE \hat{Y} = argmax\ {P(Y|X)} \\ \LARGE = argmax\ \frac{P(X, Y)}{P(X)} \\ \LARGE = argmax\ P(X, Y) Y^=argmax P(Y∣X)=argmax P(X)P(X,Y)=argmax P(X,Y)
左上角的紫色箭头: X [ k + 1 : M ] \large X_{[k+1: M]} X[k+1:M]不受 X [ 1 : k ] \large X_{[1:k]} X[1:k]的影响。
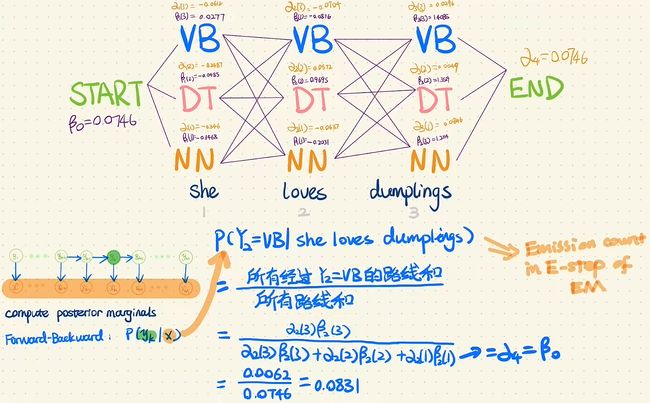
通过前向、后向算法,得到了所有的α与β值,可以直接计算边缘概率:
这就是EM算法中,E步的过程,下面通过例子讲解整个EM的过程:
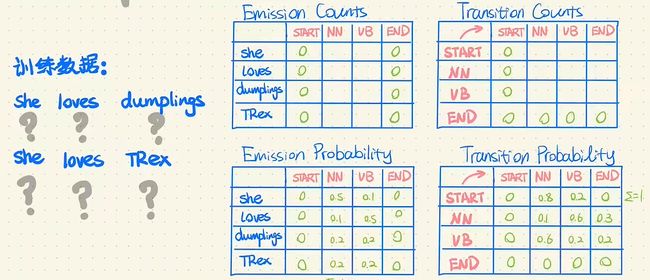
为了简单,这里假设只有NN、VB两种状态值,词表只有She、loves、dumplings、TRex。
首先通过随机初始化得到两个概率矩阵。
通过上述方法求得 P ( X , Y ) P(X,Y) P(X,Y)与 P ( Y ∣ X ) P(Y|X) P(Y∣X)
根据 P ( X , Y ) P(X,Y) P(X,Y)与 P ( Y ∣ X ) P(Y|X) P(Y∣X)求得两个Count表格并做归一化得到新的两个概率矩阵(M步)
例如:Emission Counts表格中,(NN, she)的值是 P ( Y ∣ X ) P(Y|X) P(Y∣X)中第一格里前四行和第二个里前四行加起来的(即给定词性NN,是she这个词的所有情况)。Transition Counts表格中,(start, NN)的值也是那8行加起来的(即初始状态为NN的所有情况)。依次得到整个表格后,通过归一化,得到概率矩阵。这么计算,效率非常低。通过前向、后向算法可以直接求得Counts表格中的值,例如下图的顶部所示。
其实HMM、MEMM、CRF的参数都是初始矩阵、状态转移矩阵、发射矩阵构成,区别只在于建模的方式。
HMM
生成模型
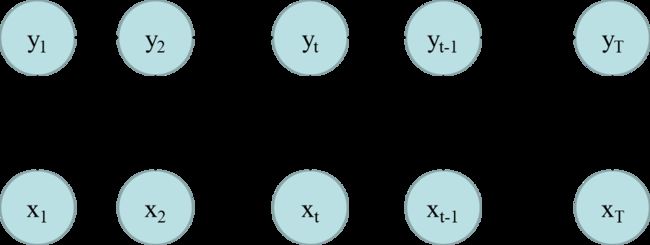
P ( X , Y ) = P ( X ∣ Y ) P ( Y ) = p ( x 1 ∣ y 1 ) p ( y 1 ) ∏ t = 2 T p ( x t ∣ y t ) p ( y t ∣ y t − 1 ) \LARGE P(X, Y) = P(X|\ Y)P(Y)\\ \LARGE= p(x_1|y_1)p(y_1)\prod_{t=2}^{T}p(x_t|\ y_t)p(y_t|\ y_{t-1}) P(X,Y)=P(X∣ Y)P(Y)=p(x1∣y1)p(y1)t=2∏Tp(xt∣ yt)p(yt∣ yt−1)
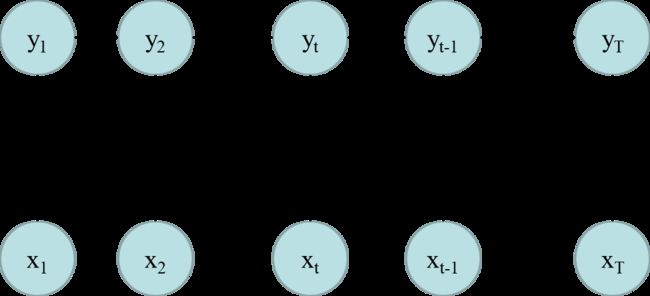
MEMM(最大熵马尔可夫模型)
判别模型
MEMM参考视频
最大熵模型推导
看上图公式,其实逻辑斯谛回归和MEMM长得很像,它们都是最大熵模型 (这里存疑),区别在于MEMM通过加入转移矩阵(或者转移特征函数)将所有的y作为一个有联系的序列。而逻辑斯谛回归中,这些y是没有联系的,只和它对应的x有联系。
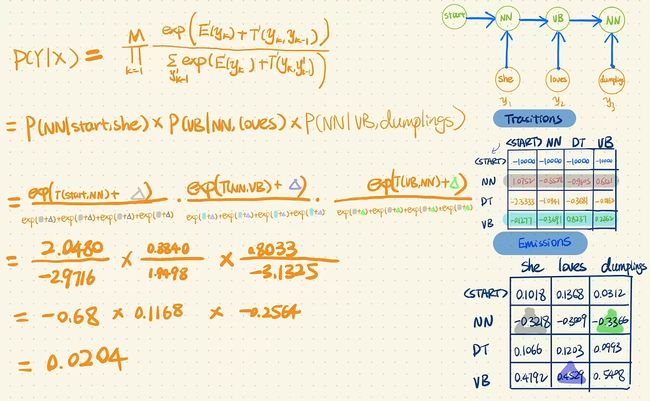
P ( Y ∣ X ) = ∏ i = 1 T p ( y i ∣ y i − 1 , x i ) = ∏ i = 1 T e x p ( E ( y i ) + T ( y i ∣ y i − 1 ) ) ∑ y ′ ∈ Y e x p ( E ( y i ) + T ( y i ∣ y i − 1 ′ ) ) \LARGE P(Y|X) = \prod_{i=1}^{T}p(y_i|y_{i-1}, x_i) \\ \LARGE = \prod_{i=1}^{T}\frac{exp(E(y_i) + T(y_i| y_{i-1}))}{\sum_{y'\in Y}exp(E(y_i)+T(y_i| y'_{i-1}))} P(Y∣X)=i=1∏Tp(yi∣yi−1,xi)=i=1∏T∑y′∈Yexp(E(yi)+T(yi∣yi−1′))exp(E(yi)+T(yi∣yi−1))
分子为特征函数,分母为归一化因子。
下面这个计算中,X=”she loves dumplings",Y=“NN VB NN”。
标注偏置问题
理论上,状态1倾向于转换为状态2,状态2倾向于转换成状态2或状态5。
但状态1的下一个状态只能是1和2,而状态2可能转换成1、2、3、4、5,一个概率由2个平分,一个概率由5个平分。所以当选择状态2时,下一个状态的概率都差不了太多,而且都不大。所以最终模型倾向于选择状态1这种转移对象很少的状态,因为它们的转移概率值通常都很大。
P(1->1->1->1) = 0.4 x 0.45 x 0.5 = 0.09
P(2->2->2->2) = 0.2 X 0.3 X 0.3 = 0.018
P(1->2->1->2) = 0.6 X 0.2 X 0.5 = 0.06
P(1->1->2->2) = 0.4 X 0.55 X 0.3 = 0.066
根据计算,发现上图这个例子得到的最优解是(1,1,1,1),但显然状态全为1是不合理的预测结果。
从转移概率角度考虑,标注偏置问题就是指:模型倾向于选择转移对象很少的状态。
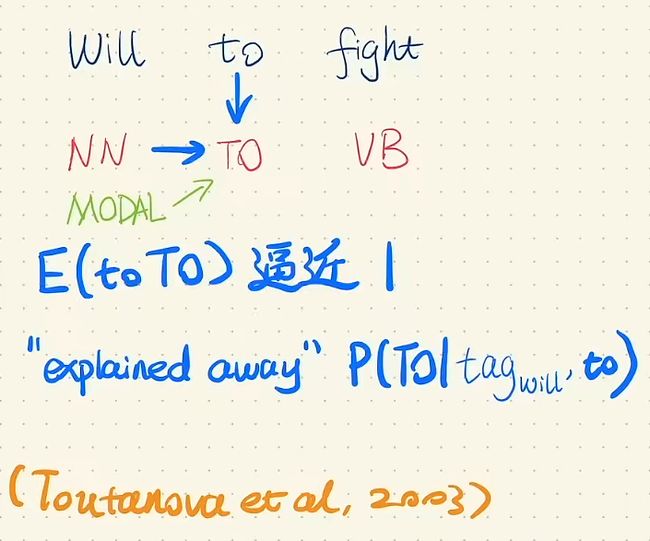
b站的二手知识,从发射概率的角度考虑:
在词性标注任务中,to只会被标注为To,它的概率值接近于1,从而上一个状态是NN还是MODAL已经不再重要。而MODAL的初始概率比较高,所以模型倾向于预测Will的标签为MODAL,但这里真实标签是NN。
个人体会(不保对):MEMM的计算是每项的概率分别做归一化,但由于数据集分布不平衡,每项得到的概率其实并不都处于同样的大小范围内,导致在某个时刻的概率值极大影响了整个序列的概率值,从而出现不合理的结果。
CRF(条件随机场)
个人体会(不保对):CRF从全局的角度进行归一化,使得其对数据集分布不那么的敏感。
CRF解决了MEMM中的标注偏置问题。
CRF参考视频
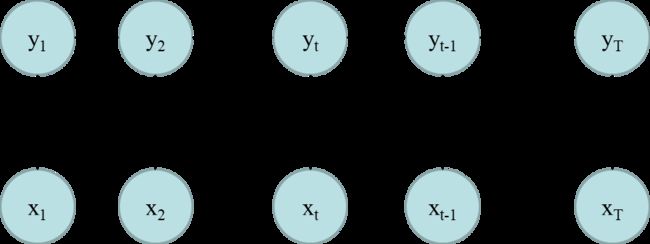
其实依旧服从一阶马尔可夫假设:当前状态受上一状态影响。去掉方向只是因为做的是全局归一化,即预测当前位置时,是考虑了整个序列的信息的。
P ( Y ∣ X ) = e x p ( ∑ t = 1 T E ( y t ) + ∑ t = 1 T T ( y t ∣ y t − 1 ) ) ∑ y 1 ′ ∈ Y ∑ y 2 ′ ∈ Y . . . ∑ y T ′ ∈ Y e x p ( ∑ t = 1 T E ( y t ′ ) + ∑ t = 1 T T ( y t ′ ∣ y t − 1 ′ ) ) \large P(Y|X) = \frac{exp(\sum_{t=1}^{T}E(y_t) + \sum_{t=1}^{T}T(y_t| y_{t-1}))}{\sum_{y_1'\in Y}\sum_{y_2'\in Y}...\sum_{y_T'\in Y}exp(\sum_{t=1}^{T}E(y'_t)+\sum_{t=1}^{T}T(y'_t| y'_{t-1}))} P(Y∣X)=∑y1′∈Y∑y2′∈Y...∑yT′∈Yexp(∑t=1TE(yt′)+∑t=1TT(yt′∣yt−1′))exp(∑t=1TE(yt)+∑t=1TT(yt∣yt−1))
P ( Y ∣ X ) = ∏ i = 1 T e x p ( E ( y i ) + T ( y i ∣ y i − 1 ) ) ∑ y ′ ∈ Y e x p ( E ( y i ) + T ( y i ∣ y i − 1 ′ ) ) \large P(Y|X) = \prod_{i=1}^{T}\frac{exp(E(y_i) + T(y_i| y_{i-1}))}{\sum_{y'\in Y}exp(E(y_i)+T(y_i| y'_{i-1}))} P(Y∣X)=i=1∏T∑y′∈Yexp(E(yi)+T(yi∣yi−1′))exp(E(yi)+T(yi∣yi−1))
前向算法与后向算法:
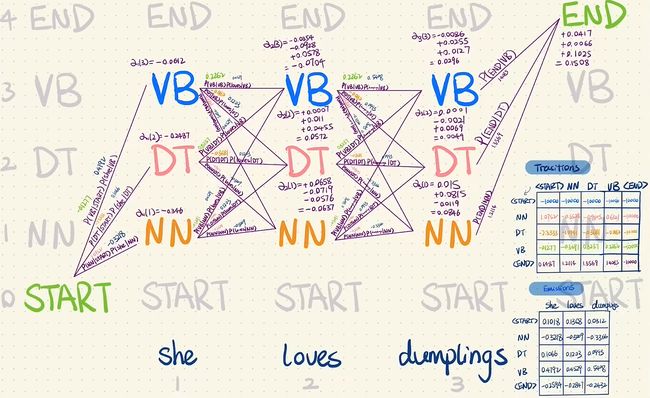
前向算法示例: