人工智能 一种现代方法 第14章 概论推理

本文旨在讲明：
1）贝叶斯网络(何谓贝叶斯网络;从网络计算概率;如何构建贝叶斯网络;网络中的条件独立性)
2）条件概率的有效表示(确定性结点;非确定性结点;连续变量)
3）贝叶斯网络的精确推理(枚举;消去重复计算)
4）贝叶斯网络的近似推理(直接采样;拒绝采样;加权;马尔科夫链采样)

贝叶斯网络

贝叶斯网络用于什么？
贝叶斯网络用于表示变量之间的依赖关系。可以本质上表示任何完全联合概率分布，在许多情况下这种表示是简明扼要的。

贝叶斯网络是什么

每个结点对应一个随机变量，这个变量可以是离散的或者连续的
一组有向边或箭头连接结点对。如果有从结点X指向结点Y的箭头，则称X是Y的一个父结点。图中没有有向回路（因此被称为有向无环图，或简写为DAG）。
每个结点Xi有一个条件概率分布P(Xi | Parents(Xi))，量化其父结点对该结点的影响。
由此可确定所有变量的完全联合概率分布

例子：防盗报警器问题的贝叶斯网络
问题：我在上班，邻居John打电话说我的闹钟响了，但邻居Mary没有打电话。有时它是由小地震引起的。有窃贼吗？
字母B、E、A、J、M分别表示Burglary(盗贼)、Earthquake、Alarm、JohnCalls以及MaryCalls

看下面两种方法对一个联合概率的计算
计算方法一：

计算方法二：

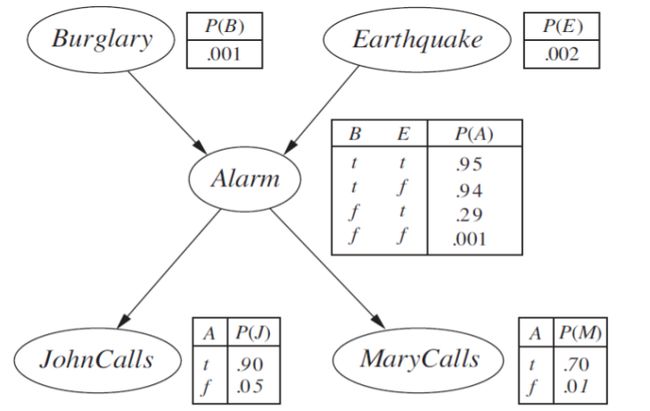
可看出结点的排序对于贝叶斯网络概率的计算具有影响。父节点排在前面时可以计算，子节点排在后面可能不利于计算。

用$P(x_1,..,x_n)$简化表示联合概率$P(X_1=x_1,...,X_n=x_n)$，则有：

$$P(x_1,..,x_n)=\prod _{i=1}^n\theta (x_i|parents(X_i))$$
其中，参数就代表$\theta (x_i|parents(X_i))$就是联合概率分别蕴含的条件概率$P(X_i|parents(X_i))$

一种构造贝叶斯网络的方法

1. 结点:首先确定变量集合。对变量进行排序得到$X_1,...,X_n$,原因排列在结果之前。虽然任何排序都是可以的，但是原因排在结果之前，可使得网络更紧致。
2. 边: i从1到n,执行:

• 从$X_1,...,X_{i-1}$中选择$X_i$的父结点的最小集合,使得$Parents(X_i)\subseteq X_{i-1},...,X_1$满足。
• 在每个父结点与$X_i$之间插入一条边。
• 条件概率表(CPTs):写出条件概率表$P(X_i|Parents(X_i))$。

构造贝叶斯网络的方法,将我们带到结论:

• 给定父结点,一个结点条件独立于它的其他祖先结点。
  P(X|U1,…Um,Parents(U1),…Parents(Um))=P(X|U1,…Um)
• 给定父结点,每个变量条件独立于它的非后代结点
  P(X|U1,…Um,Parents(Y1),…Parents(Yn))=P(X|U1,…Um)

拓扑语义蕴含了另一个重要的独立性特性：
给定一个结点的父结点、子结点、以及子结点的父结点，即给定它的马尔可夫覆盖(Markov blanket)，这个结点条件独立于网络中的所有其他结点。

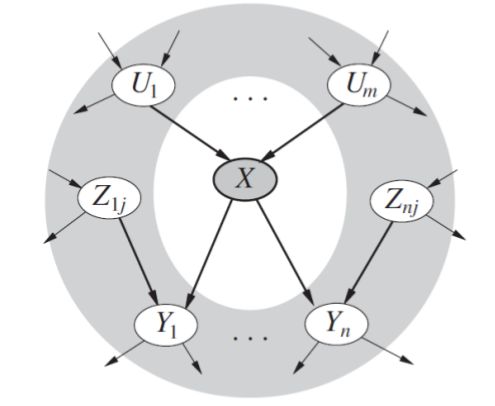
结点X条件独立于网络中除了它的马尔可夫盖的所有其他结点。

条件分布的有效表示

贝叶斯网络的精确推理

推理任务

给定一组证据变量的赋值后,计算一组查询变量的后验概率分布。

通过枚举进行推理

任何条件概率都可以通过将完全联合概率分布中的某些项相加而计算得到
$$P(X|e)=\alpha P(X,e)=\alpha \sum _{y}P(X,e,y)$$
P(x, e, y)可以写成网络中的条件概率的乘积形式

考虑查询
$$P(Burglary|JohnCalls=true,MaryCalls=true)$$

$$P(B|j,m)=\alpha P(B,j,m)=\alpha \sum _e\sum _{a}P(B,j,m,e,a)$$

Burglary = true（即b）,的情况

$$\begin{gathered} P(b|j,m)=\alpha \sum _e\sum _{a}P(b)P(e)P(a|b,e)P(j|a)P(m|a) \\ P(b|j,m)=\alpha P(b)\sum _{e}P(e)\sum _{a}P(a|b,e)P(j|a)P(m|a) \\ P(b|j,m)=\alpha \times 0.00059224 \end{gathered}$$
¬b的相应计算结果为α× 0.0014919
因此，P(B|j,m)=α<0.00059224,0.0014919>≈<0.284,0.716>
也就是说，在两个邻居都打了电话的情况下，出现盗贼的概率大约是28%。

公式：
$$P(b|j,m)=\alpha P(b)\sum _{e}P(e)\sum _{a}P(a|b,e)P(j|a)P(m|a)$$
的计算过程显示为下图中的一棵表达式树。

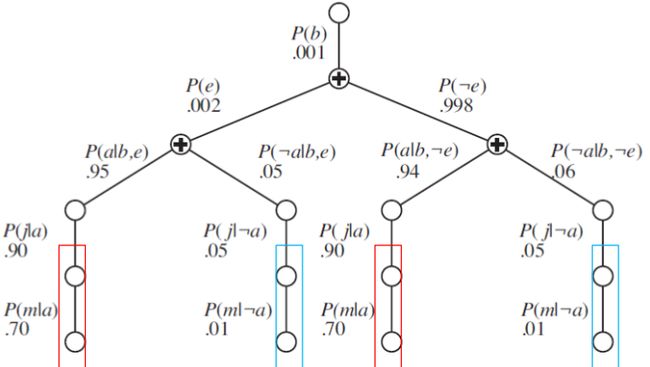
求值运算过程自顶向下，将每条路径上的值相乘，并在+号结点求和。注意到j和m有重复路径。P(j|a)P(m|a)和P(j|¬a)P(m|¬a)都分别计算了两次。

变量消元算法(避免重复计算)

变量消元算法的工作方式是按照从右到左的次序计算公式，中间结果被保存下来，而对每个变量的求和只需要对依赖于这些变量的表达式部分进行就可以了。

消元顺序

不同顺序决定了不同的时间和空间要求

贝叶斯网络的近似推理

####　蒙特卡洛算法(随机采样算法)

直接采样

####　拒绝采样

似然加权

马尔可夫链采样

Gibbs采样算法

资源分享

实验代码下载：
https://github.com/yyl424525/AI_Homework
人工智能-一种现代方法中文第三版pdf、课件、作业及解答、课后习题答案、实验代码和报告、历年考博题下载：https://download.csdn.net/download/yyl424525/11310392