机器学习-白板推导系列(三十)-生成模型(Generative Model)
机器学习-白板推导系列(三十)-生成模型(Generative Model)
30.1 生成模型的定义
前面所详细描述的模型以浅层的机器学习为主。本章将承上启下引出后面深度机器学习的部分。本小节,主要讲述的是什么是生成模型,它是不是只是生成样本,生成数据?它的任务是什么?精准的定义是什么?
这个问题实际上在之前的章节中有过详细的介绍。这里更进一步总结。之前讲过的简单的生成模型,包括:
- 高斯混合分布(GMM),GMM的主要任务是聚类,属于非监督学习;
- 而监督学习中的生成模型,最简单的有朴素贝叶斯模型,主要任务是分类。
- Logistics regression(LR)模型主要是对 P ( Y = 1 ∣ X ) P(Y=1|X) P(Y=1∣X)或 P ( Y = 0 ∣ X ) P(Y=0|X) P(Y=0∣X)条件概率进行建模,并不关心样本 X X X是什么样。
生 成 模 型 关 注 点 是 样 本 分 布 本 身 , 解 决 的 问 题 与 任 务 无 关 , 对 样 本 分 布 建 模 。 {\color{red}生成模型关注点是样本分布本身,解决的问题与任务无关,对样本分布建模}。 生成模型关注点是样本分布本身,解决的问题与任务无关,对样本分布建模。
比如:
- 简单学习中,先对 P ( X , Y ) P(X,Y) P(X,Y)建模,然后求 ∑ X P ( Y ∣ X ) \sum_X P(Y|X) ∑XP(Y∣X)来计算条件概率。
- 在无监督学习中,直接对 P ( X ) P(X) P(X)建模。有时 P ( X ) P(X) P(X)非常的复杂,直接对 P ( X ) P(X) P(X)建模非常的困难。引入隐变量(Latent) Z Z Z,对 P ( X , Z ) P(X,Z) P(X,Z)建模,然后 P ( X ) = ∑ Z P ( X ∣ Z ) P(X) = \sum_Z P(X|Z) P(X)=∑ZP(X∣Z)。
生 成 模 型 关 注 的 是 样 本 分 布 本 身 , 是 对 样 本 数 据 本 身 建 模 {\color{red}生成模型关注的是样本分布本身,是对样本数据本身建模} 生成模型关注的是样本分布本身,是对样本数据本身建模, 所 以 一 定 和 概 率 分 布 有 关 , 往 往 被 称 之 为 “ 概 率 生 成 模 型 ” 。 {\color{red}所以一定和概率分布有关,往往被称之为“概率生成模型”。} 所以一定和概率分布有关,往往被称之为“概率生成模型”。
30.2 任务角度:监督 vs 非监督
按照任务分可以将生成模型实现的功能分成: 分 类 , 回 归 , 标 记 , 降 维 , 聚 类 , 特 征 学 习 , 密 度 估 计 , 生 产 数 据 。 {\color{red} 分类,回归,标记,降维,聚类,特征学习,密度估计,生产数据。} 分类,回归,标记,降维,聚类,特征学习,密度估计,生产数据。
监 督 { 概 率 模 型 { 判 别 模 型 ( P ( Y ∣ X ) ) : L R , M E M M , C R F ; 生 成 模 型 : N B , M M , T M , N P M , F M ; 非 概 率 模 型 : P L A , S V M , K N N , T r e e M o d e l , N N . (30.1.1) \color{blue}\begin{matrix} 监督\left\{\begin{matrix} 概率模型\left\{\begin{matrix} 判别模型(P(Y|X)):LR, MEMM, CRF;\\ 生成模型:NB, MM, TM, NPM, FM;\end{matrix}\right.\\ 非概率模型 : PLA, SVM, KNN, Tree\, Model,NN.\end{matrix}\right.\end{matrix}\tag{30.1.1} 监督⎩⎨⎧概率模型{判别模型(P(Y∣X)):LR,MEMM,CRF;生成模型:NB,MM,TM,NPM,FM;非概率模型:PLA,SVM,KNN,TreeModel,NN.(30.1.1)
监 督 { 概 率 模 型 : 生 成 模 型 ; 非 概 率 模 型 : P C A , L S A , K m e a n ; (30.1.2) \color{blue}\begin{matrix} 监督\left\{\begin{matrix} 概率模型: 生成模型;\\ 非概率模型 : PCA, LSA,Kmean;\end{matrix}\right.\end{matrix}\tag{30.1.2} 监督{概率模型:生成模型;非概率模型:PCA,LSA,Kmean;(30.1.2)
-
判别模型
判别模型是对条件概率分布建模 P ( Y ∣ X ) P(Y|X) P(Y∣X),典型的有Logistics Regression,最大熵马尔可夫模型(MEMM),条件随机场(CRF)。 -
非概率模型
包括PLA,Support Vector Machines(支持向量机),KNN(K近邻网络),Tree Model,神经网络(Neural Network)。注意神经网络非概率模型,但是和判别模型并不是非黑即白的关系,也可以起到判别模型的作用。其大部分情况是发挥着非概率模型的作用。
-
非监督任务
- 非监督任务中,概率模型都是生成模型,和前文描述的监督学习中的概率模型是一样的。
- 非概率模型包括:PCA(SVD分解),LSA(潜语义分析),K-means,Auto-encoder。
-
生成模型
4.1 浅 层 的 生 成 模 型 \color{red}浅层的生成模型 浅层的生成模型
1. Naive Bayes \textbf{1. Naive Bayes} 1. Naive Bayes,此模型非常简单,主要是服从朴素贝叶斯假设。朴素贝叶斯假设描述的是: 样 本 空 间 各 维 度 之 间 相 互 独 立 \color{red}样本空间各维度之间相互独立 样本空间各维度之间相互独立, P ( X ∣ Y ) = ∏ i = 1 p P ( x i ∣ Y ) ( x ∈ R p ) P(X|Y)=\prod_{i=1}^p P(x_i|Y)(x\in R^p) P(X∣Y)=∏i=1pP(xi∣Y)(x∈Rp)。2. Mixture Model \textbf{2. Mixture Model} 2. Mixture Model,其中的典型代表是混合高斯模型(GMM),此模型主要是用于 聚 类 \color{red} 聚类 聚类。模型可以简要的表示为 P ( X ∣ Z ) ∼ P(X|Z)\sim P(X∣Z)∼ Gaussian Distribution.
3. Time-series Model \textbf{3. Time-series Model} 3. Time-series Model,最基础的有隐马尔可夫模型(HMM),卡曼滤波(Kalman Filter),粒子滤波(Particle Filter)。
4. Non-Parameteric Model \textbf{4. Non-Parameteric Model} 4. Non-Parameteric Model,此模型最重要的特点是参数空间无限化,参数不是一个确定的值,而是一个服从分布,比如Gaussian Process(GP)模型,此模型也是Bayesian Model的一种。
5. Mixed Memership Model \textbf{5. Mixed Memership Model} 5. Mixed Memership Model,其代表是LDA模型。
6. Factorial Model \textbf{6. Factorial Model} 6. Factorial Model,包括Factor Analysis(FA),概率PCA模型(P-PCA),ICA,和**稀疏编码(Sparse Coding)**等等。
上述的六种模型都是 浅 层 的 生 成 模 型 \color{red}浅层的生成模型 浅层的生成模型,简单的说就是模型的结构相对固定,变换不大,模型的层数也很较少。
4.2 D e e p 生 成 模 型 \color{red}{Deep生成模型} Deep生成模型
7. Energy based model \textbf{7. Energy based model} 7. Energy based model,包括前面讲到的,Boltzmann Machines,Sigmoid Belief Network,Deep Belief Network,Deep Boltzmann Machines。其主要是基于玻尔兹曼分布的,而实际上玻尔兹曼分布为 exp { E ( θ ) } \exp\{\mathrm{E}(\theta)\} exp{E(θ)},可以看成是熵的形式。8. Variational Automation Encoder \textbf{8. Variational Automation Encoder} 8. Variational Automation Encoder,变分自编码器。
9. GAN \textbf{9. GAN} 9. GAN,生成对抗神经网络。
10. Auto-regressive Model \textbf{10. Auto-regressive Model} 10. Auto-regressive Model。
11. Flow-base model \textbf{11. Flow-base model} 11. Flow-base model,基于流的模型。
D e e p 生 成 模 型 \color{red}{Deep生成模型} Deep生成模型模型结构变化较大,而且层数较多。深度生成模型中,经常将神经网络和传统概率相结合。Deep之前的模型,比较固化,基本是用来解决特定的问题。
- P C A → P → F A PCA \rightarrow P \rightarrow FA PCA→P→FA;
- K − m e a n s → G M M K-means \rightarrow GMM K−means→GMM
- A u t o − e n c o d e r → V A E Auto-encoder \rightarrow VAE Auto−encoder→VAE
- L S A → p L S A → L D A LSA \rightarrow pLSA \rightarrow LDA LSA→pLSA→LDA
30.3 模型表示,推断和学习
上一小节从监督学习或者非监督学习的角度介绍了生成模型,这小节将从模型,推断和学习表示的角度分别介绍生成模型。
30.3.1 模型表示(形神兼备)
首先从模型表示角度介绍,我们可以用 “ 形 神 兼 备 ” \color{red}“形神兼备” “形神兼备”四个字来描述。
-
形 \color{red}形 形
“形”包括以下几个方面,可以理解为生成模型的 概 率 图 \color{red}概率图 概率图表示形式:1. 点:Discrete vs Continuous \textbf{1. 点:Discrete vs Continuous} 1. 点:Discrete vs Continuous,从点的角度出发,也就是说节点的变量是离散随机变量还是连续随机变量。
2. 边:Directed Model vs Undirected Model \textbf{2. 边:Directed Model vs Undirected Model} 2. 边:Directed Model vs Undirected Model,从有向图和无向图的角度进行分类,有向图是贝叶斯模型,无向图是马尔可夫模型,这是从边的角度进行分析。
3. 隐变量:Latent Variational Model vs Fully Observed Model \textbf{3. 隐变量:Latent Variational Model vs Fully Observed Model} 3. 隐变量:Latent Variational Model vs Fully Observed Model,区分为所有变量可完全观测或者含有部分隐变量。
4. 层次:Shadow vs Deep \textbf{4. 层次:Shadow vs Deep} 4. 层次:Shadow vs Deep,这个是根据网络的层数来确定的。
5.节点: Sparse vs Dense \textbf{5.节点: Sparse vs Dense} 5.节点: Sparse vs Dense,此分类标准根据节点之间连接的权重稠密或者稀疏而定的。比如,Boltzmann Machines之间权重的连接就比HMM之间要稠密的多,最稠密的当然是完全图了。
-
神 \color{red}神 神
这个从“神”的角度来分,有一点抽象,哈哈哈!主要从以下两个方面来理解。6. 参数:Parameteric Model vs Non-Parameteric Model \textbf{6. 参数:Parameteric Model vs Non-Parameteric Model} 6. 参数:Parameteric Model vs Non-Parameteric Model,此分类描述的是参数是确定的,还是一个分布,参数不确定,比如,高斯过程就是Non-Parameteric Model,每个时刻的参数都服从不同的高斯分布。
7.建模对象: Implicit Density Model vs Explicit Density Model \textbf{7.建模对象: Implicit Density Model vs Explicit Density Model} 7.建模对象: Implicit Density Model vs Explicit Density Model,Implicit Density Model(隐性密度模型)中最典型的就是GAN。Explicit Model的特征是对 P ( X ) P(X) P(X)建模,而Implicit Model不直接考虑对 P ( X ) P(X) P(X)的建模,只需要可从目标分布中采样即可。比如,GAN通过从目标分布中采样,来建立一个虚拟的分布。
30.3.2 模型推断
推断就很简单了,基本就是从计算可行性分析, 8.追踪: Tractable vs Intractable \textbf{8.追踪: Tractable vs Intractable} 8.追踪: Tractable vs Intractable。
30.3.3 学习
学习的主要可以分为: 9.似然: Likelihood-based Model vs Likelihood-free Model \textbf{9.似然: Likelihood-based Model vs Likelihood-free Model} 9.似然: Likelihood-based Model vs Likelihood-free Model,极大似然估计求解,是使log似然达到最大之后,用求得的参数来进行采样。而Likelihood-free方法中,学习采用的方法和Likelihood无关,比如:GAN。
30.3.4 小结
我们从模型表示,推断和学习表示的角度分别介绍生成模型,可以得到以下9种分类。以后分析一个模型,可以从讲的9个角度出发:
- Discrete vs Continuous
- Directed Model vs Undirected Model
- Latent Variational Model vs Fully Observed Model
- Shadow vs Deep
- Sparse vs Dense
- Parameteric Model vs Non-Parameteric Model
- Implicit Model vs Explicit Model
- Tractable vs Intractable
- Likelihood-based Model vs Likelihood-free Model
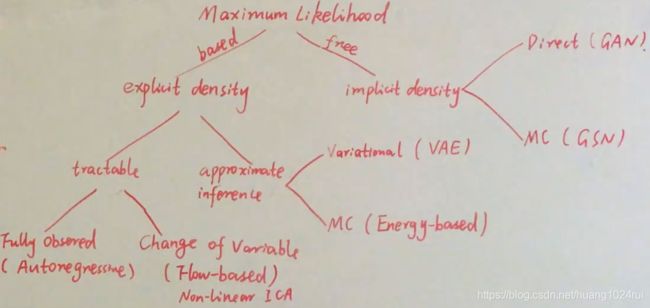
30.4 Maximum Likelihood
从Likelihood-based Model和Likelihood-free Model两个方面分,是目前比较流行的一种分法。
30.4.1 Likelihood-based Model(Explicit Density Model)
这是显式的估计概率密度函数,也就是Explicit Density Model。根据其是否可计算大致可以分成两类,tractable 和 intractable(Approximate Inference)。
- Tractable可以分为:Fully observed 和change of variable(Flow-based model)。
- Fully observed模型结构相对很简单,典型算法Autoregression Model。
- Change of variable典型算法Flow-based model。
Change of variable(Flow-based model)简要的说明:假如 P ( X ) P(X) P(X)非常复杂,那么我们可以对一个简单的分布 P ( Z ) P(Z) P(Z)建模,然后寻找一个 X ↦ Z X \mapsto Z X↦Z的映射 X = g ( Z ) X=g(Z) X=g(Z)。那么,可得 Z = g − 1 ( X ) Z = g^{-1}(X) Z=g−1(X)。此模型的主要目的就是学习这个映射 g ( Z ) g(Z) g(Z),可以得到
P X ( X ) = P Z ( g − 1 ( X ) ) P_X(X) = P_Z(g^{-1}(X)) PX(X)=PZ(g−1(X))
参数计算为 ∂ g − 1 ( X ) ∂ X \frac{\partial g^{-1}(X)}{\partial X} ∂X∂g−1(X)。
- Approximate Inference,包括两种,1. 于随机采样:MCMC,这是一种Energy Based Model。2. 确定性的变分推断,典型的算法有VAE。
30.4.2 Likelihood-free Model(Implicite Density Model)
Implicite表示直接从样本采样,不显示的概率密度函数,也就是不直接对概率密度函数建模。可分为:Direct和MC。
- Direct常见算法:直接从样本分布中采样的GAN;
- MC(通过模拟一个分布来直接进行采样,不需要通过MCMC采样。样本直接生成分布。)常见算法:Mento Calro算法,GSN等。
30.4.3 小结
我觉得主要是从函数学习方法的角度,来进行分类,也就是是否计算似然函数。个人觉得Likelihood-free Model是目前很重要的研究,以我做的科研为例,我觉得从未知分布中采样来逼近目标分布非常重要,如果给目标分布确定的形式会造成算法的局限性,所有舍弃分布的具体,使用采样来逼近非常重要,现在比较流行的有分布式强化学习中的分位点回归法。
30.5 概率图 vs 神经网络
概率图模型和神经网络之间并不是一个非黑即白的区别,它们之间有区别也有联系,但是很多部分同学都搞不清他们之间的区别。
- 概 率 图 模 型 是 P ( X ) 的 表 示 \color{red}概率图模型是P(X)的表示 概率图模型是P(X)的表示;
- 神 经 网 络 即 时 一 个 函 数 逼 近 器 \color{red}神经网络即时一个函数逼近器 神经网络即时一个函数逼近器,对于一个输入的 X X X,得到输出的 Y Y Y,中间的部分都是权重。
所以,他们两压根不是一个东西,概率图模式是对 P ( X ) P(X) P(X)来建模,典型的概率生成模型。
概率图模型中主要讨论的是Bayesian Network,Boltzmann Machines(无向图模型);神经网络是广义连接主义,确定NN有CNN,RNN。在本节中,仅比较Beyesian Network(有向图模型)和Neural Network(NN)。
30.5.1 Bayesian vs NN
本小节将从表示,推断,学习和适合问题四个角度出发进行比较。
-
模型表示
-
Bayesian Network(概率图)是从结构化,权值之间相对稀疏,而且通常层数比较浅(浅层),符合 条 件 独 立 假 设 \color{red}条件独立假设 条件独立假设。其中最重要的是Bayesian Network具有可解释性,建模的时候具有真实的物理意义。
-
而NN(计算图)的层数,往往会比较深,而且权值连接很稠密,没有具体的物理意义。
有的小伙伴会说,NN也具有可解释性,比如神经网络类似为一个滤波器,其可以抽象出更多的高层信息。这个东西,其实只是我们一厢情愿的,这个意义并不是在建模的时候赋予的。而是我们发现了其好的效果之后,在这里强行解释,有点“马后炮”的味道。 N N 的 可 解 释 性 一 般 未 知 \color{red}NN的可解释性一般未知 NN的可解释性一般未知。
-
-
模型推断
- Bayesian Network中包括精确推断和近似推断,有MCMC和变分等方法。还有极大似然估计等等。
- 神经网络的推断方法就非常的简单了,输入输出即可,没有太多的研究意义。
-
模型学习
- Bayesian Network中常见的解决方法有Log似然梯度,EM算法等。
- NN中常用的方法是梯度下降,由于这个层数很多,节点很多的时候求导很不好求,于是引入了BP算法。其实BP算法是一种高效的求导方法,其实 B P 算 法 = 链 式 求 导 法 则 + 动 态 规 划 \color{red}{BP算法 = 链式求导法则+动态规划} BP算法=链式求导法则+动态规划。动态规划什么意思,就是递归+缓存。
实际上,可以感觉到Bayesian Network和神经网络都不是一个level的东西。
- 概 率 图 是 一 个 模 型 层 次 的 , 是 对 数 据 样 本 的 建 模 。 \color{red}{概率图是一个模型层次的,是对数据样本的建模。} 概率图是一个模型层次的,是对数据样本的建模。
- 而 神 经 网 络 中 被 称 之 为 计 算 图 , 完 全 就 是 来 计 算 用 的 。 \color{red}{而神经网络中被称之为计算图,完全就是来计算用的。} 而神经网络中被称之为计算图,完全就是来计算用的。
- 适合的问题
- Bayesian Network更适合解决High Level Reasoning的问题,适合于做原因推断。
- 而NN更适合解决Low Level Reasoning的问题, 不 适 合 做 原 因 推 断 \color{red}{不适合做原因推断} 不适合做原因推断,只能由于解决弱推理问题。其更适合表示学习。
30.5.1 小结
本章的内容比较简单,基本就是从表示,推断,学习和适合问题四个角度出发进行比较概率图模型和神经网络模型。其实这两个东西都不是一个level的,主要区别是概率图模型是对样本数据的建模,而神经网络只是一个函数逼近器而已。
30.6 Stochastic Back Propagation (Reparametrization Trick)
本章主要介绍的是:神经网络和概率图模型结合到一起。神经网络用 Y = f ( X ; θ ) Y=f(X;\theta) Y=f(X;θ)函数逼近(用NN去逼近一个概率分布 P ( X ) P(X) P(X))。
把他们两结合到一起就是随机后向传播(Stochastic Back Propagation),或者称之为重参数技巧(Reparametrization Trick)。
30.6.1 正常情况下简单举例
-
假设 P ( Y ) P(Y) P(Y)是目标分布,其中 P ( Y ) ∼ N ( μ , σ 2 ) \color{red}P(Y)\sim \mathcal{N}(\mu,\sigma^2) P(Y)∼N(μ,σ2)。我们之前是怎么采样的呢?是先从一个简单的高斯分布中进行采样 Z ∼ N ( 0 , 1 ) Z\sim \mathcal{N}(0,1) Z∼N(0,1),然后令 Y = μ + σ Z Y = \mu + \sigma Z Y=μ+σZ,相当于一个二元一次变换。得到采样方法:
{ z ( i ) ∼ N ( 0 , 1 ) y ( i ) = μ + σ z ( i ) (30.6.1) \left\{\begin{array}{ll} z^{(i)} \sim \mathcal{N}(0,1) & \\ y^{(i)} = \mu + \sigma z^{(i)} & \\ \end{array}\right.\tag{30.6.1} {z(i)∼N(0,1)y(i)=μ+σz(i)(30.6.1)
很自然的可以将此函数看成: y = f ( μ , σ , z ) \color{red}y=f(\mu, \sigma, z) y=f(μ,σ,z)。这是一个关于 z z z的函数, μ , σ \mu, \sigma μ,σ假设是确定性变量,也就是:当 z z z确定时,函数的值是确定的。那么,算法的目标:找到一个函数映射 z ↦ y \color{red}z\mapsto y z↦y,函数的参数为 { μ , σ } \color{red}\{ \mu,\sigma \} {μ,σ}。 -
假设, J ( y ) \color{red}J(y) J(y)是目标函数, θ = { μ , σ } \theta = \{ \mu,\sigma \} θ={μ,σ}。那么梯度求导方法为:
∇ J ( y ) ∇ θ = ∇ J ( y ) ∇ y ∇ y ∇ θ (30.6.2) \frac{\nabla J(y)}{\nabla \theta} = \frac{\nabla J(y)}{\nabla y} \frac{\nabla y}{\nabla \theta}\tag{30.6.2} ∇θ∇J(y)=∇y∇J(y)∇θ∇y(30.6.2)
30.6.2 条件概率密度函数
- 假设目标分布为 P ( Y ∣ X ) = N ( X ; μ , σ 2 ) \color{red}P(Y|X)=\mathcal{N}(X;\mu,\sigma^2) P(Y∣X)=N(X;μ,σ2), Z ∼ N ( 0 , 1 ) Z \sim \mathcal{N}(0,1) Z∼N(0,1)进行采样,可得:
Y = μ ( X ) + σ ( X ) Z (30.6.3) Y=\mu(X) + \sigma(X)Z\tag{30.6.3} Y=μ(X)+σ(X)Z(30.6.3)
实际上将 X X X看成输入, Z Z Z看成是噪声, Y Y Y则是输出。神经网络参数为 θ \theta θ。逻辑关系为:
Y = μ θ ( X ) + σ θ ( X ) Z (30.6.4) \color{red}Y = \mu_\theta(X) + \sigma_\theta(X)Z\tag{30.6.4} Y=μθ(X)+σθ(X)Z(30.6.4)
网络的模型如下:
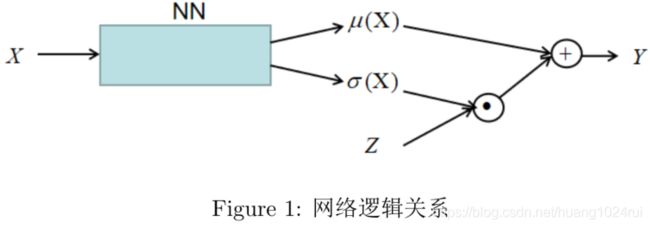
其中, μ ( X ) = f ( X ; θ ) , σ ( X ) = f ( X ; θ ) \color{red}\mu(X)=f(X;\theta),\sigma(X)=f(X;\theta) μ(X)=f(X;θ),σ(X)=f(X;θ)。损失函数为:
L θ ( Y ) = ∑ i = 1 N ∥ y − y ( i ) ∥ 2 (30.6.5) \color{red}L_\theta(Y) = \sum_{i=1}^N \|y-y^{(i)}\|^2\tag{30.6.5} Lθ(Y)=i=1∑N∥y−y(i)∥2(30.6.5)
链式求导法则为:
∇ J θ ( Y ) ∇ θ = ∇ J θ ( Y ) ∇ Y ∇ Y ∇ μ ∇ μ ∇ θ + ∇ J θ ( Y ) ∇ Y ∇ Y ∇ σ ∇ σ ∇ θ (30.6.6) \color{red}\frac{\nabla J_\theta(Y)}{\nabla \theta} = \frac{\nabla J_\theta(Y)}{\nabla Y}\frac{\nabla Y}{\nabla \mu}\frac{\nabla \mu}{\nabla \theta} + \frac{\nabla J_\theta(Y)}{\nabla Y}\frac{\nabla Y}{\nabla \sigma}\frac{\nabla \sigma}{\nabla \theta}\tag{30.6.6} ∇θ∇Jθ(Y)=∇Y∇Jθ(Y)∇μ∇Y∇θ∇μ+∇Y∇Jθ(Y)∇σ∇Y∇θ∇σ(30.6.6)
这样就可以做到用NN来近似概率密度函数,观测这个式子发现 Y Y Y必须要是连续可微的,不然怎么求 ∇ Y ∇ σ \frac{\nabla Y}{\nabla \sigma} ∇σ∇Y。实际上这个模型可以被写为:- P ( Y ∣ X ; θ ) P(Y|X;\theta) P(Y∣X;θ),将 X , θ X,\theta X,θ合并到一起就是 w w w;
- 也可以被写为 P ( Y ∣ w ) P(Y|w) P(Y∣w)。
30.6.3 小结
这小结从用神经网络来近似概率分布的角度分析两种概率分布模型,简单的高斯分布和条件高斯模型。并简要的介绍了其链式求导法则。
30.7 总结
本章节主要是对于概率生成模型进行了一个全面的介绍,起到一个承上启下的作用。
1. 回顾了之前写到的浅层概率生成模型,并引出了接下来要介绍的深度概率生成模型。
2. 并从任务(监督 vs 非监督),模型表示,模型推断,模型学习四个方面对概率生成模型做了分类。
3. 并从极大似然的角度重新对模型做了分类。
4. 介绍了概率图模型和神经网络的区别,我觉得其中最重要的是,概率图模式是对样本数据建模,其图模型有具体的意义;而神经网络只是函数逼近器,只能被称为计算图。
5. 最后,介绍了重参数技巧,用神经网络逼近概率分布。