假设检验及例题讲解
本博客结合浙大假设检验的课程PPT，以举例子的方式通俗易懂地展示了如何使用常见的几种假设检验以及使用技巧。
目录
-
-
- 先举一个例子
-
- 1 假设检验定义
-
- 1.2 假设检验的假设
-
- 1.2.1 第一类错误（弃真错误）、第二类错误（取伪错误）
- 1.2.2 显著性水平
- 1.2.3 P值
- 1.3 基本思想（一定要看！！！）
- 2 检验方式
-
- 2.1 检验统计量
- 2.2 拒绝域
- 2.3 接受域
- 概括
- 3 假设检验步骤
-
- 3.1 两种假设检验
-
- 3.1.1 一个总体参数的假设检验
- 4 正态总体均值的假设检验
-
- 4.1 单个正态总体的均值检验
-
- 4.1.1 u检验 （方差已知）
- 4.1.2 t检验 （方差未知）
- 4.2 两个正太总体的均值检验
-
- 4.2.1 U检验（方差已知）
- 4.2.2 t检验（方差未知）
- 5 正太总体方差的假设检验
-
- 5.1 单个正态总体均值未知的的方差检验
- 5.2 两个正态总体的方差检验
-
- 5.2.1 均值未知的方差双边检验
- 5.2.2 均值未知的方差==单边检验==
先举一个例子
我们在生活中经常会遇到对一个总体数据进行评估的问题，但我们又不能直接统计全部数据，这时就需要从总体中抽出一部分样本，用样本来估计总体情况。
举一个简单的例子：
然后我们来分析一下：
如何操作：
原假设： H 0 : E X = 75 ; H 1 : E X ≠ 75 H_0:EX=75; H_1:EX≠75 H0:EX=75;H1:EX=75
假定原假设正确，则 X ∼ N ( 75 , σ 2 ) \mathbf{X}\sim \mathbf{N}(75, \sigma^{2}) X∼N(75,σ2)，于是 T 统计量 拒绝域：
T = X ˉ − 75 S / n ∼ t ( n − 1 ) T=\frac{\bar{X}-75}{S/\sqrt{n}} \sim t(n-1) T=S/nXˉ−75∼t(n−1)
可得：
P { X ˉ − 75 S / n ≥ t α / 2 } = α P\{\frac{\bar{X}-75}{S/\sqrt{n}} \ge t_{\alpha/2}\}=\alpha P{S/nXˉ−75≥tα/2}=α
如果某一样本的观测值 ∣ X ˉ − 75 S / n ∣ ≥ t α / 2 \lvert \frac{\bar{X}-75}{S/\sqrt{n}} \rvert \ge t_{\alpha/2} ∣S/nXˉ−75∣≥tα/2，则拒绝 H 0 H_0 H0。
注意蓝色字体，是如何定义哪些名词的：
1 假设检验定义
假设检验是先对总体参数提出一个假设值，然后利用样本信息判断这一假设是否成立？
1.2 假设检验的假设
由定义可知，我们需要对结果进行假设，然后拿样本数据去验证这个假设。
所以做假设检验时会设置两个假设：
一种叫原假设，也叫零假设，用H0表示。原假设一般是统计者想要拒绝的假设（但也不绝对），这样通过证伪原假设就可以反证统计者真正想要接受的假设。原假设的设置一般为：等于（更多情况）=、大于等于>=、小于等于<=。
另外一种叫备择假设，用H1表示。备则假设是统计者想要接受的假设。备择假设的设置一般为：不等于、大于>、小于< （没有等于哦）。
为什么统计者想要拒绝的假设放在原假设呢？因为原假设备被拒绝如果出错的话，只能犯第I类错误，而犯第I类错误的概率已经被规定的显著性水平所控制。
1.2.1 第一类错误（弃真错误）、第二类错误（取伪错误）
我们通过样本数据来判断总体参数的假设是否成立，但样本时随机的，因而有可能出现小概率的错误。这种错误分两种，一种是弃真错误，另一种是取伪错误。
弃真错误 也叫第I类错误或α错误：它是指 原假设实际上是真的，但通过样本估计总体后，拒绝了原假设。明显这是错误的，我们拒绝了真实的原假设，所以叫弃真错误，这个错误的概率我们记为α。这个值也是显著性水平，在假设检验之前我们会规定这个概率的大小。（类似于假阴性）
原假设H0为真，而检验结果为拒绝H0，记其概率为 α \alpha α，即： P { 拒绝 H 0 ∣ H 0 为真 } = α P\{拒绝H0|H0为真\}=\alpha P{拒绝H0∣H0为真}=α，这里的 α \alpha α 这就是我们说的显著性水平。
取伪错误 也叫第II类错误或β错误：它是指 原假设实际上假的，但通过样本估计总体后，接受了原假设。明显者是错误的，我们接受的原假设实际上是假的，所以叫取伪错误，这个错误的概率我们记为β。（类似于假阳性）
原假设H0不符合实际，而检验结果为接受H0，极其概率为 β \beta β，即： P { 接受 H 0 ∣ H 0 为假 } = β P\{接受H0|H0为假\}=\beta P{接受H0∣H0为假}=β
希望：犯两类错误的概率越小越好，但样本容量一定的前提下，不可能同时降低 α 和 β \alpha 和 \beta α和β。
原则：保护原假设，即限制 α \alpha α 的前提下，使 β \beta β 尽可能地小。
现在清楚原假设一般都是想要拒绝的假设了么？因为原假设备被拒绝，如果出错的话，只能犯弃真错误，而犯弃真错误的概率已经被规定的显著性水平所控制了。这样对统计者来说更容易控制，将错误影响降到最小。
可以这么概括两类错误：
1.2.2 显著性水平
显著性水平 α \alpha α 为犯第一类错误的概率。
显著性水平是指当原假设实际上正确时，检验统计量落在拒绝域的概率，简单理解就是犯弃真错误的概率。这个值是我们做假设检验之前统计者根据业务情况定好的。
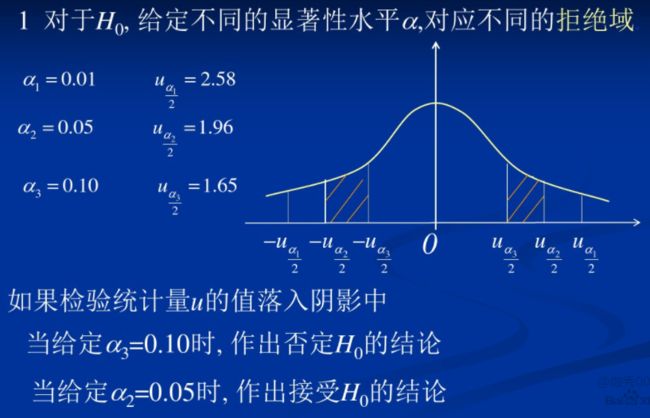
显著性水平α越小，犯第I类错误的概率自然越小，一般取值：0.01、0.05、0.1等
当给定了检验的显著水平a=0.05时，进行双侧检验的Z值为1.96，t值为 。
当给定了检验的显著水平a=0.01时，进行双侧检验的Z值为2.58 。
当给定了检验的显著水平a=0.05时，进行单侧检验的Z值为1.645 。
当给定了检验的显著水平a=0.01时，进行单侧检验的Z值为2.33
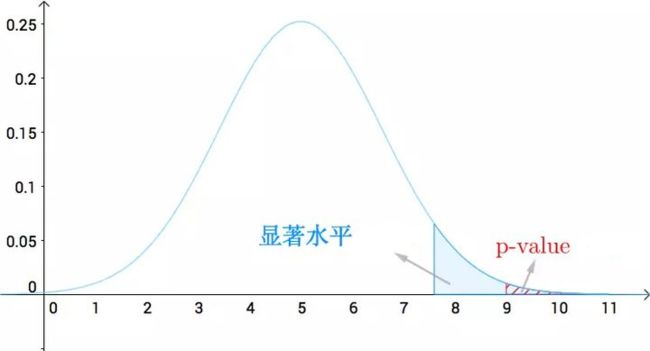
1.2.3 P值
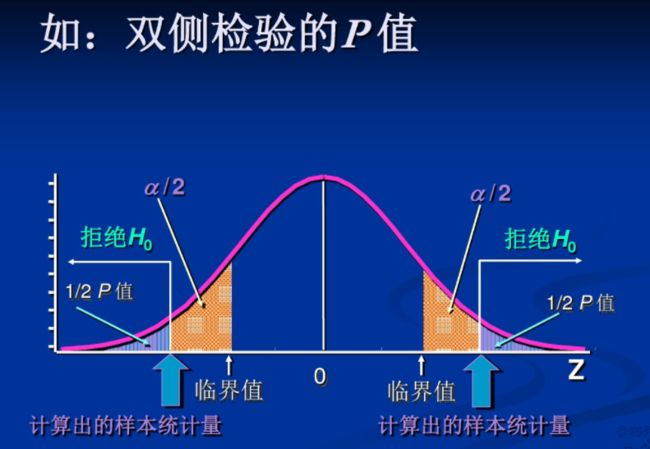
一个重要概念：p值 ：用于确定我们是否拒绝H0，是一个概率值，如图当P值小于显著水平时，说明检验的统计量落入拒绝域中，拒绝零假设。
1.3 基本思想（一定要看！！！）
参数的假设检验：已知总体的分布类型，对分布函数或密度函数中的某些参数提出假设，并检验。
基本原则——小概率事件在一次实验中是不可能发生的。
思想：如果原假设成立，那么某个分布已知的统计量在某个 区域（拒绝域，参考2.2节） 内取值的 概率 α \alpha α（显著性水平，又称检验水平） 应该较小，如果样本的观测数值落在这个小概率区域内，则原假设不正确，所以拒绝原假设；否则，接受原假设。
2 检验方式
检验方式分为两种：双侧检验和单侧检验。单侧检验又分为两种：左侧检验和右侧检验。
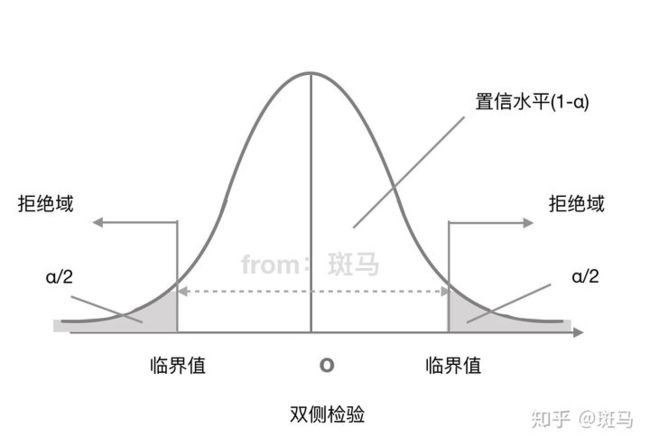
双侧检验：备择假设没有特定的方向性，形式为“≠”这种检验假设称为双侧检验
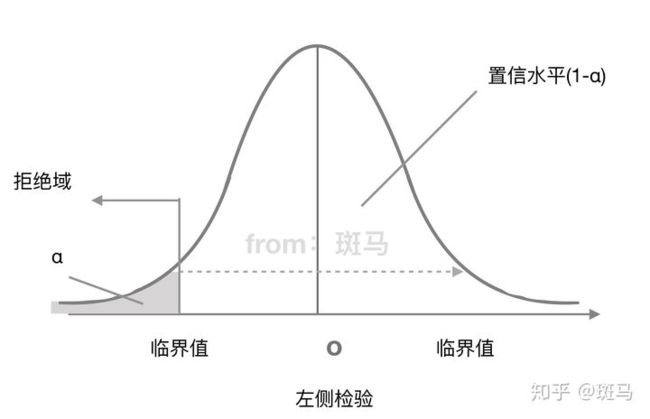
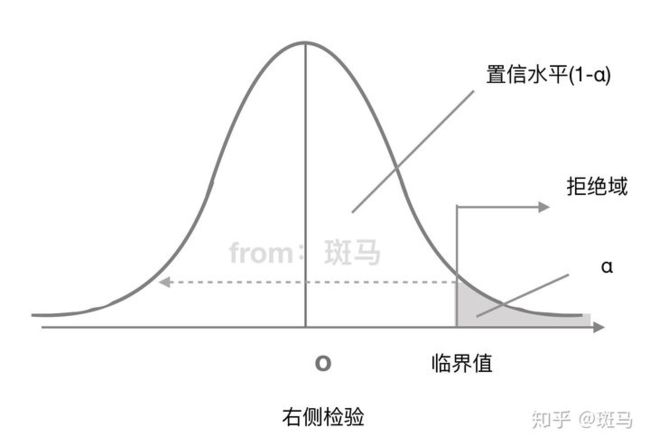
单侧检验：备择假设带有特定的方向性 形式为">“”<"的假设检验，称为单侧检验 "<"称为左侧检验 ">"称为右侧检验
2.1 检验统计量
定义：据以对原假设和备择假设作出决策的某个样本统计量，称为检验统计量。
2.2 拒绝域
定义：拒绝域是由显著性水平围成的区域
拒绝域的功能主要用来判断假设检验是否拒绝原假设的。如果样本观测计算出来的检验统计量的具体数值落在拒绝域内，就拒绝原假设，否则不拒绝原假设。给定显著性水平α后，查表就可以得到具体临界值，将检验统计量与临界值进行比较，判断是否拒绝原假设。
双侧检验拒绝域：
左侧检验拒绝域：
右侧检验拒绝域：
2.3 接受域
定义：保留原假设的样本观察值所组成的区域。
概括
3 假设检验步骤
-
提出原假设H0与备择假设H1；
-
确定拒绝域；
-
给定显著性水平 α \alpha α；
-
计算在此 α \alpha α下H0成立条件下的临界值（上侧 α \alpha α分位数，或双侧 α \alpha α分位数）；
-
计算统计量的样本观测值，与4计算的临界值进行比较，如果落在拒绝域内，则拒绝原假设，否则接受原假设。
说明：
3.1 两种假设检验
假设检验根据业务数据分为两种：一个总体参数的假设检验和两个总体参数的假设检验
一个总体参数的假设检验：只有一个总体的假设检验
举个例子：学而思App原版本1转化率为 19%，学而思App版本2开发完成后，直接全量发布整体上线，过一段时间后统计转化率为27%，我们想判断版本2是否比版本1好，这时我们做的假设检验总体只有1个，全部用户。对于总体只有一个的称为一个总体参数的假设检验。
两个总体参数的假设检验：有两个总体的假设检验
同样的例子：学而思App版本1和学而思App版本2同时上线，流量各50%，这时我们做的假设检验总体有2个，分别为命中版本1的全部用户与命中版本2的全部用户。
两种假设检验的检验统计量计算方式有所不同，所以做区分描述。
3.1.1 一个总体参数的假设检验
大小样本：样本量大于等于30的样本称为大样本，样本量小于30的样本称为小样本。
一个总体参数的大样本（ n > = 30 n>=30 n>=30）假设检验方法：
假设形式：
双侧检验：H0 ： μ = μ 0 \mu=\mu_0 μ=μ0 ， H1 ： μ ≠ μ 0 \mu \neq \mu_0 μ=μ0 ；
左侧检验：H0 ： μ ≥ μ 0 \mu\ge\mu_0 μ≥μ0 ， H1 ： μ < μ 0 \mu<\mu_0 μ<μ0 ;
右侧检验：H0 ： μ ≤ μ 0 \mu\le\mu_0 μ≤μ0 ， H1 : μ > μ 0 \mu>\mu_0 μ>μ0 ;
检验统计量：
α 与拒绝域 \alpha 与拒绝域 α与拒绝域
双侧检验：![[公式]](http://img.e-com-net.com/image/info8/927cbd694bbc48daba36a40a979a17fa.jpg){kind=small}
左侧检验： ![[公式]](http://img.e-com-net.com/image/info8/cb8efe1421d0442d84ac3a13f72b4a9b.jpg){kind=small}
右侧检验： ![[公式]](http://img.e-com-net.com/image/info8/faa2d3f317af4ad187ec018f140838a7.jpg){kind=small}
P值决策：
P< [公式] ，拒绝H0
4 正态总体均值的假设检验
可以分为：
1.单个正态总体的均值检验
2.两个正态总体的均值检验
4.1 单个正态总体的均值检验
4.1.1 u检验 （方差已知）
以双边检验为例：
在方差已知的情况下，我们需要用到 u检验。
来看看例题：
上题是双边检验的场景，下面我们来看一下单边检验：
4.1.2 t检验 （方差未知）
前面讨论的是方差已知的情况，接下来讨论方差未知的情况，此时我们要用到 t检验。
还是先来看看双边检验的情况：
来看个例子：
同样的，我们要看一下单边检验的场景：
4.2 两个正太总体的均值检验
同样，也要分成方差已知和方差未知的情况。
4.2.1 U检验（方差已知）
1.96来自u检验中双侧检验查表可得：
4.2.2 t检验（方差未知）
来看一看例子：
在来看个例子：
5 正太总体方差的假设检验
第4章讲的是 对于均值的假设检验，现在来看一下对于方差的假设检验。
同样，也分为：
1.单个正态总体的方差检验
2.两个正态总体的方差检验
5.1 单个正态总体均值未知的的方差检验
先来看一看双边检验：
来看看例子：
这道题对均值和方差都做了检验
我们来看看他是怎么做的？
5.2 两个正态总体的方差检验
5.2.1 均值未知的方差双边检验
来看个例题：
5.2.2 均值未知的方差单边检验
看完了这些例题，大家一定熟悉掌握了假设检验的精髓了吧？欢迎在评论区交流哦~
参考：
https://zhuanlan.zhihu.com/p/35032285
https://zhuanlan.zhihu.com/p/86178674
https://max.book118.com/html/2020/0704/6023221123002214.shtm