2019 Domain-Specific Batch Normalization for Unsupervised Domain Adaptation

论文地址：https://arxiv.org/pdf/1906.03950v1.pdf
代码地址：https://github.com/wgchang/DSBN

1 研究动机与研究思路

研究动机： 因为源域和目标域领域具有不同的特征，通过分离领域特定信息和领域不变信息可以获得更好的泛化性能。为了分离领域特定信息进行无监督的领域自适应，本文提出了一种新的基于特定域批归一化的无监督域适应框架DSBN,通过在卷积神经网络中专门设置批量归一化层来适应两个领域，同时允许它们共享所有其他模型参数。
研究思路： DSBN利用BN参数捕获领域特殊性信息，并利用该参数将领域特殊性数据转换为域不变表示。DSBN层由批归一化( Batch Normalization，BN )的两个分支组成，每个分支单独负责一个域（两个域在两个阶段都有单独的批归一化层）。
算法普遍适用于各种具有BN层的无监督域适应深度神经网络。

2 主要工作

本文的主要工作：

• 提出了一种新的基于DSBN的无监督领域自适应框架，它是一种适用于各种深度神经网络模型的域适应通用方法。
• 引入了一种包含伪标签估计和多任务分类的DSBN两阶段学习方法，该方法自然地集成到现有的无监督领域自适应方法中。
• 通过其直接的扩展提供了一种多源的无监督领域自适应的通用算法。

3 方法

3.1 主要框架

本文提出一个基于DSBN的无监督域适应的两阶段框架，首先在目标域中生成未标记数据的伪标注，然后使用伪标注学习一个完全监督的模型。具体来说，第一阶段使用无监督的域适应算法(例如MSTN [ 27 ]或CPUA [ 14 ] )来估计目标域中的示例的伪标签。第二阶段，利用源域和目标域的数据，在完全监督的情况下训练一个包含DSBN层的多任务分类网络，其中第一阶段生成的伪标注被分配给目标域数据。为了进一步提高准确率，迭代第二阶段训练并细化目标域中示例的标签。

3.2 准备工作

3.2.1 参数说明

${\mathcal{X}}_S$表示有标记的源域，${\mathcal{X}}_T$表示无标记的目标域，其中$n_S$ 和 $n_T$分别表示${\mathcal{X}}_S$和${\mathcal{X}}_T$的势。本文的目标是在完全监督的基础上，通过迁移从源域学习到的分类知识，对目标域中的实例进行分类。本节将详细讨论两种最新的方法来集成特定领域批归一化技术。

3.2.2 移动语义迁移网络(Moving Semantic Transfer Network)

MSTN [ 27 ]基于未标记目标域样本的伪标注，提出了语义匹配损失函数来跨域对齐相同类的质心。总损失函数$\mathcal{L}$的形式定义为
$$\mathcal{L}={\mathcal{L}}_{\mathrm{cls}}\left({\mathcal{X}}_S\right)+\lambda {\mathcal{L}}_{\mathrm{da}}\left({\mathcal{X}}_S,{\mathcal{X}}_T\right)+\lambda {\mathcal{L}}_{\mathrm{sm}}\left({\mathcal{X}}_S,{\mathcal{X}}_T\right)$$
分类损失${\mathcal{L}}_{\mathrm{cls}}$为源域数据集的交叉熵损失，领域对抗损失${\mathcal{L}}_{\mathrm{da}}$使得网络混淆了域成员。语义匹配损失${\mathcal{L}}_{\mathrm{sm}}\left({\mathcal{X}}_S,{\mathcal{X}}_T\right)$将相同类别的质心跨域对齐。需要注意的是，用伪标签来计算语义匹配损失。
直观地看，损失函数鼓励两个域具有相同的分布，特别是通过添加对抗和语义匹配损失项。因此，基于损失函数的学习网络可以应用于目标领域的实例。

3.2.3 类预测不确定性对齐(Class Prediction Uncertainty Alignment)

CPUA [ 14 ]是一种非常简单的方法，它只对齐域之间的类概率。CPUA解决了两个域中的类不平衡问题，并引入了一个类加权损失函数来利用类先验知识。
设$p_S(c)=n_S^c/n_S$ 是具有类标号$c$的源域样本的分数，$p_T(c)=n_T^c/n_T$为目标样本中伪标记为$c$的比例。$n_T^c$ 表示$\left\{x\in {\mathcal{X}}_T\mid y(x)=c\right\}$,的势，其中$y(x)={\mathrm{argmax}}_{i\in C}F(x)[i]$ .则每个域的类权重分别为：
$$w_S(x,y)=\frac{{\max }_{y^{\prime }}{p}_S\left(y^{\prime }\right)}{p_S(y)}$$
和
$$w_T(x)=\frac{{\max }_{y^{\prime }}{p}_T\left(y^{\prime }\right)}{p_T(y(x))}$$
它们的总损失函数可以写为：
$$\mathcal{L}={\mathcal{L}}_{\text{cls }}\left({\mathcal{X}}_S\right)+\lambda {\mathcal{L}}_{\mathrm{da}}\left({\mathcal{X}}_S,{\mathcal{X}}_T\right)$$
where
$$\begin{array}{rl}{\mathcal{L}}_{\mathrm{cls}}\left({\mathcal{X}}_S\right)& =\frac{1}{n_S}\sum _{(x,y)\in {\mathcal{X}}_S}{w}_S(x,y)\ell (F(x),y),\\ {\mathcal{L}}_{\mathrm{da}}\left({\mathcal{X}}_S,{\mathcal{X}}_T\right)& =\frac{1}{n_S}\sum _{(x,y)\in {\mathcal{X}}_S}{w}_S(x,y)\ell (D(F(x)),1),\\ & +\frac{1}{n_T}\sum _{x\in {\mathcal{X}}_T}{w}_T(x)\ell (D(F(x)),0).\end{array}$$
注意到$F(\cdot )$一个分类网络， $\ell (\cdot ,\cdot )$表示交叉熵损失，$D(\cdot )$是一个域判别器。

3.3 领域特定的批归一化

本部分对批归一化( Batch Normalization，BN )与DSBN进行比较，然后介绍了DSBN及其对多源域适应的扩展。

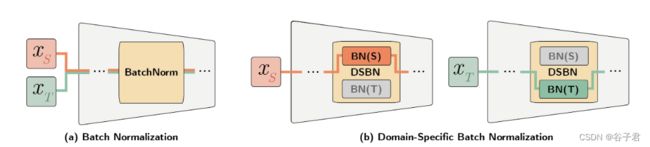
图1 BN与DSBN的区别。DSBN层由批归一化层中的两个分支组成，一个分支用于源域( S )，另一个分支用于目标域( T )。每个输入实例根据其领域选择其中一个分支。在具有DSBN层的域自适应网络中，除DSBN层外的所有参数在两个域中共享，有效地学习了两个域中共有的信息，同时通过DSBN层的域特定BN参数有效地捕获了域特定的属性。

3.3.1 批量归一化BN

BN是深度网络中广泛使用的训练技术。一个BN层在每一个通道维度的N个示例中白化激活（whitens activations），并使用仿射参数$\gamma$和$\beta$变换白化激活。
用 $\mathrm{x}\in {\mathbb{R}}^{H\times W\times N}$ 表示每个通道的激活，BN表示为
$$\mathrm{BN}(\mathrm{x}[i,j,n];\gamma ,\beta )=\gamma \cdot \hat{\mathrm{x}}[i,j,n]+\beta ,$$
其中
$$\hat{\mathbf{x}}[i,j,n]=\frac{\mathrm{x}[i,j,n]-\mu }{\sqrt{{\sigma }^2+ϵ}}.$$
一个小批量内激活的均值和方差，$\mu$ 和$\sigma$，计算得到
$$\begin{array}{rl}\mu & =\frac{{\sum }_n{\sum }_{i,j}\mathrm{x}[i,j,n]}{N\cdot H\cdot W},\\ {\sigma }^2& =\frac{{\sum }_n{\sum }_{i,j}(\mathrm{x}[i,j,n]-\mu {)}^2}{N\cdot H\cdot W}.\end{array}$$
$ϵ$ 是一个小的常数以避免被零除。
在训练过程中，BN通过更新因子为$\alpha$的指数移动平均来估计整个激活的均值和方差，记为$\bar{\mu }$和$\bar{\sigma }$。形式上，给定第$t^{\text{th }}$个小批量，其均值和方差为
$$\begin{array}{rl}{\bar{\mu }}^{t+1}& =(1-\alpha ){\bar{\mu }}^t+\alpha {\mu }^t,\\ {\left({\bar{\sigma }}^{t+1}\right)}^2& =(1-\alpha ){\left({\bar{\sigma }}^t\right)}^2+\alpha {\left({\sigma }^t\right)}^2.\end{array}$$
在测试阶段，BN使用估计的均值和方差进行归一化输入激活。需要注意的是，如果域偏移显著，同时共享源域和目标域的均值和方差是不合适的。

3.3.2 特定领域批标准化DSBN

DSBN是利用为每个领域预留的多组BN [ 5 ]实现的。形式上，DSBN为每个域标签$d\in \{S,T\}$分配特定于域的仿射参数${\gamma }_d$和${\beta }_d$。令${\mathbf{x}}_d\in {\mathbb{R}}^{H\times W\times N}$ 表示每个通道的激活属于一个域标签d，则DSBN层可以写为

$${\mathrm{DSBN}}_d\left({\mathbf{x}}_d[i,j,n];{\gamma }_d,{\beta }_d\right)={\gamma }_d\cdot {\hat{\mathbf{x}}}_d[i,j,n]+{\beta }_d$$
其中
$${\hat{\mathbf{x}}}_d[i,j,n]=\frac{{\mathbf{x}}_d[i,j,n]-{\mu }_d}{\sqrt{{\sigma }_d^2+ϵ}}$$
$$\begin{array}{rl}{\mu }_d& =\frac{{\sum }_n{\sum }_{i,j}{\mathbf{x}}_d[i,j,n]}{N\cdot H\cdot W}\\ {\sigma }_d^2& =\frac{{\sum }_n{\sum }_{i,j}{\left({\mathbf{x}}_d[i,j,n]-{\mu }_d\right)}^2}{N\cdot H\cdot W}\end{array}$$
在训练过程中，DSBN通过更新因子为$\alpha$的指数移动平均法分别估计每个域的激活均值和方差
$$\begin{array}{rl}{\bar{\mu }}_d^{t+1}& =(1-\alpha ){\bar{\mu }}_d^t+\alpha {\mu }_d^t\\ {\left({\bar{\sigma }}_d^{t+1}\right)}^2& =(1-\alpha ){\left({\bar{\sigma }}_d^t\right)}^2+\alpha {\left({\sigma }_d^t\right)}^2\end{array}$$
每个域的估计均值和方差用于DSBN测试阶段对应域的算例。
本文期望DSBN通过分别估计每个域的批统计量和学习仿射参数来捕获特定域的信息。本认为，DSBN可以让网络更好地学习领域不变的特征，因为通过从给定领域捕获的统计信息和学习的参数，可以有效地去除网络中的特定领域信息。
DSBN容易嵌入现有的深度神经网络进行无监督域适应。现有的分类网络$F(\cdot )$ 可以通过将所有BN层替换为DSBN层并使用带有领域标签的数据训练整个网络来转换为领域特定的网络。域特定网络用$F_d(\cdot )$表示，它依赖于域变量 $d\in \{S,T\}$，专门化于源域或目标域。

3.3.3 多源域适应扩展

DSBN通过在其中添加更多的域分支，很容易扩展为多源无监督域适应。适用于多源域适应的损失函数可以简单地由所有源域的损失之和定义，如下：
$$\mathcal{L}=\frac{1}{\left|{\mathcal{D}}_S\right|}\sum _i^{|{\mathcal{D}}_S|}\left({\mathcal{L}}_{\text{cls }}\left({\mathcal{X}}_{S_i}\right)+{\mathcal{L}}_{\text{align }}\left({\mathcal{X}}_{S_i},{\mathcal{X}}_T\right)\right)$$
其中， ${\mathcal{D}}_S=\left\{{\mathcal{X}}_{S_1},{\mathcal{X}}_{S_2},\dots \right\}$ 是源域集合，${\mathcal{L}}_{\text{align }}$ 可以是源域和目标域对齐的任意一种损失。其余训练过程与单源域适应情况相同。

3.4 基于DSBN的领域自适应

DSBN是一种通用的无监督域自适应技术，通过批量归一化可以集成到基于深度神经网络的各种算法中。本文的框架分两个阶段训练用于无监督域适应的深度网络。在第一阶段，本文训练一个现有的无监督域适应网络来生成目标域数据的初始伪标注。第二阶段以源域中的背景真值和目标域中的伪标注作为监督学习两个域的最终模型，其中目标域中的伪标注在训练过程中被逐级细化。
两个阶段的网络都加入了DSBN层，更有效地学习领域不变表示，从而更好地适应目标域。为了进一步提高准确率，本文可以进行第二阶段训练的额外迭代，其中伪标注使用前一次迭代中的结果进行更新。

3.4.1 阶段1:训练初始伪标签

本文选择了两种最先进的模型作为初始伪标签生成器：MSTN [ 27 ]和CPUA [ 14 ]。用DSBNs替换它们的BN层，使它们能更有效地学习域不变表示。然后通过网络的原始损失和学习策略进行训练。一个训练好的初始伪标签生成器记为$F_T^1$。

3.4.2 第二阶段：带伪标签的自训练

图2 第二阶段训练概述。为了对目标域样本使用中间伪标签，使用第一阶段训练的网络$F_T^1(x)$作为第二阶段的伪标签。在此阶段，网络仅在两个域中使用分类损失进行训练。
在第二阶段，本文利用来自两个域的数据和它们的标签，利用丰富的域不变表示，在完全监督的情况下训练两个域的最终模型。网络使用两个分类损失进行训练，一个用于具有真实标签的源域，另一个用于具有伪标注的目标域，得到的网络用$F_d^2$表示，其中$d\in \{S,T\}$。总损失函数由来自两个域的两个损失项的简单求和给出如下：
$$\mathcal{L}={\mathcal{L}}_{\text{cls }}\left({\mathcal{X}}_S\right)+{\mathcal{L}}_{\text{cls }}^{\text{pseudo }}\left({\mathcal{X}}_T\right)$$
其中
$$\begin{array}{rl}{\mathcal{L}}_{\text{cls }}\left({\mathcal{X}}_S\right)& =\sum _{(x,y)\in {\mathcal{X}}_S}\ell \left(F_S^2(x),y\right),\\ {\mathcal{L}}_{\text{cls }}^{\text{pseudo }}\left({\mathcal{X}}_T\right)& =\sum _{x\in {\mathcal{X}}_T}\ell \left(F_T^2(x),y^{\prime }\right)\end{array}$$
式中：$\ell (\cdot ,\cdot )$ 为交叉熵损失，$y^{\prime }$ 表示分配给目标域样本$x\in {\mathcal{X}}_T$的伪标签。伪标签$y^{\prime }$由F1T初始化，并由$F_T^2$逐步精化：
$$y^{\prime }=\underset{c\in C}{\mathrm{argmax}}\left\{(1-\lambda )F_T^1(x)[c]+\lambda F_T^2(x)[c]\right\},$$
其中$F_T^i(x)[c]$表示由$F_T^i$给出的类别$c$的预测分数，$\lambda$是一个在训练过程中从0到1逐渐变化的权重因子。由于 $F_T^2$在训练的同时参与伪标签的生成，因此该方法可以看作是一种self-supervised训练。在训练的早期阶段，由于$F_T^2$的预测可能是不可靠的，所以本文对$F_T^1$给出的初始伪标注赋予了更多的权重。然后权重λ逐渐增大，在训练的最后阶段，伪标签完全依赖于$F_T^2$。本文遵循[ 3 ]来抑制潜在的噪声伪标注；适应因子$\lambda$按$\lambda =\frac{2}{1+\exp (-\gamma \cdot p)}-1$递增， $\gamma =10$.。
由于 $F_T^2$利用$F_T^1$给出的合理初始伪标注进行训练，而$F_T^1$仅依靠弱信息进行域对齐，因此 $F_T^2$比$F_T^1$总体上能更准确地识别目标域图像。为了进一步提高初始伪标注的精度，利用$F_T^2$估计更精确的初始伪标注。因此，本文迭代地执行第二阶段过程，其中初始伪标注使用前一次迭代中模型的预测结果进行更新。本文实证地观察到这种迭代方法对于提高目标域的分类精度是有效的。

4 实验

4.1 实验设置

4.1.1 数据集

使用三个数据集进行实验：VisDA-C [ 16 ]，Office-31 [ 17 ]和Office - Home [ 26 ]。

• VisDA - C是面向2017年视觉域适应挑战赛的大规模基准数据集。它由合成和真实两个域组成，从MS - COCO [ 8 ]数据集中获取了12个常见对象类的152 409张合成图像和55 400张真实图像。
• Office - 31是域适应的标准基准，它由31个类别的3个不同域组成：2817张图像的Amazon ( A )、795张图像的Webcam ( W )和498张图像的DSLR ( D )。
• Office-Home [ 26 ]有4个域：Art ( Ar )，2 427张图像；剪纸艺术( Cl )，4 365张图像；Product ( Pr )，4 439张图像；Real-World ( Rw )，4 357张图像。每个领域包含65类常见日常用品。

4.1.2 实现细节

使用ResNet - 101作为VisDA - C数据集的主干网络，使用ResNet - 50作为Office - 31和Office - Home数据集的主干网络。所有网络都有BN层，并在ImageNet上进行预训练。为了比较BN层和DSBN层的截然不同，所有实验都为每个域构建了小批量并分别forward。批次大小设置为40。
采用Adam优化器，${\beta }_1=0.9,{\beta }_2=0.999$。设定阶段1和阶段2的初始学习率${\eta }_0=1.0\times 10^{-4}$ 和 $5.0\times 10^{-5}$。如文献[ 3 ]所述，学习率由公式 ${\eta }_p=\frac{{\eta }_0}{(1+\alpha p{)}^{\beta }}$调整，其中$\alpha =10$, $\beta =0.75$，$p$表示从0到1线性变化的训练进度。优化器的最大迭代次数设置为50000次。

4.2 结果

在标准的基准数据集上展示了基于单源域和多源域适应的实验结果。
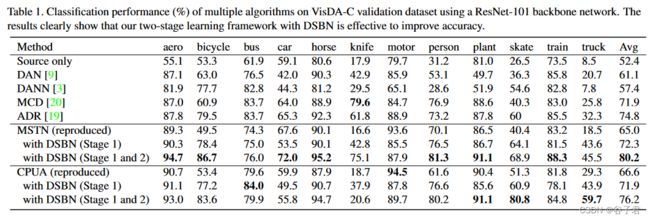
VisDA - C表1量化了MSTN和CPUA作为初始伪标签生成器的方法的性能，并与VisDA - C数据集上的最新记录进行了比较。表中’ DSBN ( Stage 1 ) ‘表示我们用DSBNs替换BN层并进行第一阶段训练，’ DSBN (第一阶段和第二阶段) '表示我们同时进行第一阶段和第二阶段训练。我们提出的方法通过将DSBNs应用到基线模型中，显著且持续地提高了准确率，并在与MSTN结合时达到了最先进的性能[ 27 ]。模型可靠地识别了刀、人、滑冰和卡车等hard classes。

Office - 31表2给出了在Office - 31数据集上使用MSTN和CPUA的总体评分。在两个阶段训练的DSBN模型都取得了最好的性能，并且始终优于两个基线模型。表2还表明，框架可以成功应用于当前的域适应算法，并极大地提升了性能。

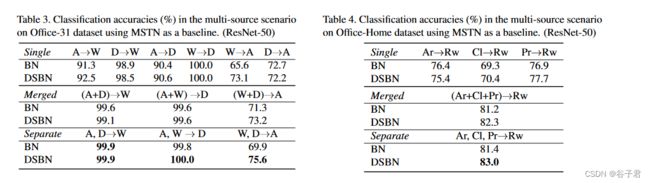
多源域表3和表4分别给出了Office - 31和Office - Home数据集上的多源域适配结果。为了比较多源与单源域适应，我们将单源结果报告在表的顶部作为" Single “，并附加两个不同的多源场景：” Merged “和” Separation “。” Merged “是指来自多个源域的数据被合并并构建一个新的更大的源域数据集，而” Separation "则表示每个源域被单独考虑。在单独的情况下，网络中总共有|DS| +1个域和相同数量的DSBN分支。虽然当目标任务容易时，BN和DSBN之间存在边际性能增益，但模型在所有设置下都一致优于BN模型。特别地，对于表3中任务’A’的hard域适应，源域分离的DSBN明显优于合并的情况。这一结果意味着DSBN在多源域适应任务中也具有优势。不存在DSBN的情况下，单独情形并不总是优于合并情形。

4.3 分析

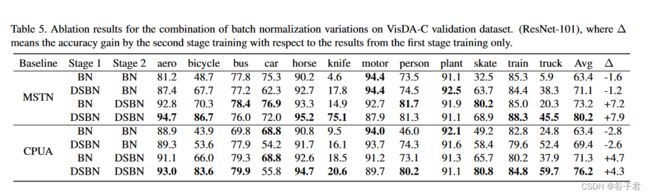
消融研究进行消融实验，以分析DSBN相对BN的效果。表5汇总了以MSTN和CPUA为基线架构在VisDA - C数据集上的消融结果，其中表中最后一列给出了第二阶段训练相对于第一阶段训练结果的精度增益。我们测试了几种不同训练程序的组合进行两阶段训练。这一结果直接表明，DSBN在两个训练过程中都起到了至关重要的作用。另一个重要的方面是，DSBN的第二阶段训练额外提高了成绩，但第二阶段的普通BN没有帮助。这意味着在训练阶段分离领域特定信息有助于得到可靠的伪标注。值得注意的是，特别是对于hard classes，这样的倾向更加明显。

特征可视化图4是在VisDA - C数据集上，以MSTN为基线，可视化BN (左)和DSBN (右)的实例嵌入。我们观察到，通过集成DSBN，同一类别中两个域的示例更好地对齐，这意味着DSBN是学习域不变表示的有效方法。

迭代学习采用第一阶段得到的网络作为第二阶段的伪标签，第二阶段学习到的网络比伪标签更强。因此，通过迭代地应用第二阶段学习过程来获得进一步的性能提升，其中当前迭代中的伪标注由上一阶段的结果给出。为了验证这个想法，我们使用MSTN作为基线算法在VisDA - C数据集上评估每次迭代中的分类精度。如表6所示，第二阶段的迭代学习随着迭代的进行精度逐渐提高。

5 结论

我们提出了用于无监督域适应的域特定批标准化。所提出的方法具有独立的批标准化层分支，每个域一个，同时跨域共享所有其他参数。这种思想普遍适用于具有批量归一化层的深度神经网络。将该方法与两阶段训练策略应用于最近的两种无监督域适应算法MSTN和CPUA，并在标准的基准数据集上展示了出色的性能。