时间序列预测方法之 DeepState

本文链接：个人站 | 简书 | CSDN
版权声明：除特别声明外，本博客文章均采用 BY-NC-SA 许可协议。转载请注明出处。

最近打算分享一些基于深度学习的时间序列预测方法。这是第二篇。

今次介绍的是 Amazon 在 NIPS 2018 上发表的文章 Deep State Space Models for Time Series Forecasting。

状态空间模型（State Space Models）起源于控制工程领域，典型的应用包括卡尔曼滤波等。时间序列分析中的一些经典方法，如 ARIMA、Holt-Winters’ 等，都可以改写成状态空间模型。状态空间模型对每个时间序列单独建模，无法利用序列之间相似的模式，因而对历史数据较少的序列往往无能为力。

DeepState 将状态空间模型与深度学习结合起来。先用循环神经网络将特征映射为状态空间模型的参数，再使用状态空间模型预测序列在每个时间步上取值的概率分布。所有的时间序列共享网络本身的参数，而每个时间序列都有独立的状态空间参数。这样一来，既能从大量的序列和特征中学习到相似的模式，又能使模型具有一定的可解释性。

Model

通常来说，状态空间模型包含一个状态转移方程和一个观测模型，前者描述了隐藏状态随时间变化的规律 $p(l_t|l_{t-1})$，后者概括了给定隐藏状态下观测值的条件概率分布 $p(z_t|l_t)$，其中隐藏状态 $l_t\in {\mathbb{R}}^L$。

DeepState 使用的是线性高斯状态空间模型，其状态转移方程形如¹

$$l_t=F_t{l}_{t-1}+w_t{\epsilon }_t,{\epsilon }_t\sim N(0,1)$$
观测模型形如
$$z_t=H_t{l}_t+b_t+v_t{ϵ}_t,{ϵ}_t\sim N(0,1)$$
其中 $F_t\in {\mathbb{R}}^{L\times L}$ 为状态转移矩阵，$w_t\in {\mathbb{R}}_{+}^L$ 是状态转移噪声的强度，$H_t\in {\mathbb{R}}^{1\times L}$ 和 $b_t\in \mathbb{R}$ 是观测模型的权重和偏置，$v_t\in {\mathbb{R}}_{+}$ 是观测噪声的强度。初始状态 $l_0\sim N({\mu }_0,diag({\sigma }_0^2))$。

综上，线性高斯状态空间模型的参数为 ${\Theta }_t=(F_t,H_t,w_t,b_t,v_t,{\mu }_0,{\sigma }_0),\forall t>0$。

DeepState 模型的结构如下图所示。先用循环神经网络计算 $h_t=\mathrm{R}\mathrm{N}\mathrm{N}(h_{t-1},x_t)$，再用 $h_t$ 计算状态空间模型的参数 ${\Theta }_t=\Psi (h_t)$，最后计算似然 $p_{SS}(z_{1:T}|{\Theta }_{1:T})$，通过最大化对数似然来学习网络的参数。

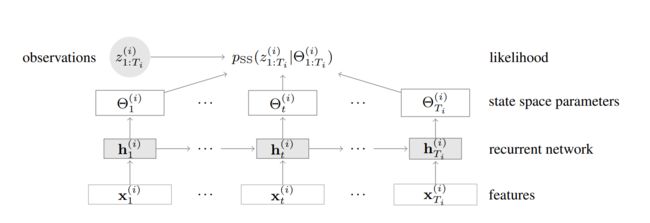
似然函数可以分解为
$$p_{SS}(z_{1:T}|{\Theta }_{1:T})=\prod _{t}p(z_t|z_{1:t-1},\Theta )$$
参考我们在《卡尔曼滤波简介》中给出的推导，可以很容易得到
$$p(z_t|z_{1:t-1})=N(H_t{\hat{l}}_{t|t-1}+b_t,S_t)$$
式中的参数可以通过以下递推关系
$$\begin{array}{rl}{\hat{l}}_{t|t-1}& =F_t{\hat{l}}_{t-1|t-1}\\ P_{t|t-1}& =F_t{P}_{t-1|t-1}{F}_t^{\top }+w_t{w}_t^{\top }\\ {\tilde{y}}_t& =z_t-H_t{\hat{l}}_{t|t-1}-b_t\\ S_t& =H_t{P}_{t|t-1}{H}_t^{\top }+v_t{v}_t^{\top }\\ K_t& =P_{t|t-1}{H}_t^{\top }{S}_t^{-1}\\ {\hat{l}}_{t|t}& ={\hat{l}}_{t|t-1}+K_t{\tilde{y}}_t\\ P_{t|t}& =P_{t|t-1}-K_t{H}_t{P}_{t|t-1}\end{array}$$
计算得到。其中 ${\hat{l}}_{0|0}={\mu }_0$，$P_{0|0}=diag({\sigma }_0^2)$。

预测阶段与之前介绍的 DeepAR 类似，都是使用祖先采样方法获取一批预测区间内每个时间步上的样本点，然后利用样本计算感兴趣的统计量。

Code

这里给出一个基于 TensorFlow 构建的简单 demo。

import numpy as np

import tensorflow as tf
import tensorflow_probability as tfp

class DeepState(tf.keras.models.Model):
    """
    DeepState 模型
    """
    def __init__(self, lstm_units, latent_dim):
        super().__init__()
        
        self.latent_dim = latent_dim
        self.output_dim = 1
        
        # 注意，文章中使用了多层的 LSTM 网络，为了简单起见，本 demo 只使用一层
        self.lstm = tf.keras.layers.LSTM(lstm_units, return_sequences=True, return_state=True)
        self.dense_l_prior = tf.keras.layers.Dense(latent_dim)
        self.dense_P_prior = tf.keras.layers.Dense(latent_dim, activation='softplus')
        self.dense_F = tf.keras.layers.Dense(latent_dim * latent_dim)
        self.dense_H = tf.keras.layers.Dense(output_dim * latent_dim)
        self.dense_b = tf.keras.layers.Dense(output_dim)
        self.dense_w = tf.keras.layers.Dense(latent_dim, activation='softplus')
        self.dense_v = tf.keras.layers.Dense(output_dim, activation='softplus')
    
    def call(self, inputs, initial_state=None, prior=True):
        batch_size, time_steps, _ = inputs.shape
        
        outputs, state_h, state_c = self.lstm(inputs, initial_state=initial_state)
        state = [state_h, state_c]
            
        F = tf.reshape(self.dense_F(outputs), [batch_size, time_steps, self.latent_dim, self.latent_dim])
        H = tf.reshape(self.dense_H(outputs), [batch_size, time_steps, self.output_dim, self.latent_dim])
        
        b = tf.expand_dims(self.dense_b(outputs), -1)
        w = tf.expand_dims(self.dense_w(outputs), -1)
        v = tf.expand_dims(self.dense_v(outputs), -1)
        
        Q = tf.matmul(w, tf.transpose(w, [0, 1, 3, 2]))
        R = tf.matmul(v, tf.transpose(v, [0, 1, 3, 2]))
        
        params = [F, H, b, Q, R]
        
        if prior:
            l = tf.expand_dims(self.dense_l_prior(outputs[:, :1, :]), -1)
            P = tf.linalg.diag(self.dense_P_prior(outputs[:, :1, :]))
            params += [l, P]
        
        return [params, state]

def kalman_step(F, H, b, Q, R, l, P, z=None):
    """
    卡尔曼滤波的单步操作
    """
    sampling = z is None

    l = tf.matmul(F, l)
    P = tf.matmul(tf.matmul(F, P), tf.transpose(F, [0, 1, 3, 2])) + Q
    z_pred = tf.matmul(H, l) + b
    S = tf.matmul(tf.matmul(H, P), tf.transpose(H, [0, 1, 3, 2])) + R
    if sampling:
        z = tfp.distributions.Normal(z_pred, S).sample()
    else:
        log_prob = tfp.distributions.Normal(z_pred, S).log_prob(z)
    K = tf.matmul(tf.matmul(P, tf.transpose(H, [0, 1, 3, 2])), tf.linalg.inv(S))
    y = z - z_pred
    l = l + tf.matmul(K, y)
    P = P - tf.matmul(tf.matmul(K, H), P)
    
    if sampling:
        return [l, P, z]
    return [l, P, log_prob]

def kalman_filtering(F, H, b, Q, R, l, P, z=None):
    """
    卡尔曼滤波
    """
    time_steps = F.shape[1]
    if z is None:
        samples = []
        for t in range(time_steps):
            Ft = F[:, t:t+1, :, :]
            Ht = H[:, t:t+1, :, :]
            bt = b[:, t:t+1, :, :]
            Qt = Q[:, t:t+1, :, :]
            Rt = R[:, t:t+1, :, :]
            l, P, zt = kalman_step(Ft, Ht, bt, Qt, Rt, l, P)
            samples.append(zt)
        return samples
    else:
        log_probs = []
        for t in range(time_steps):
            Ft = F[:, t:t+1, :, :]
            Ht = H[:, t:t+1, :, :]
            bt = b[:, t:t+1, :, :]
            Qt = Q[:, t:t+1, :, :]
            Rt = R[:, t:t+1, :, :]
            zt = z[:, t:t+1, :, :]
            l, P, log_prob = kalman_step(Ft, Ht, bt, Qt, Rt, l, P, zt)
            log_probs.append(log_prob)
        loss = -tf.reduce_sum(log_probs)
        return l, P, loss

实例化模型，指定优化器，就可以训练了：

LSTM_UNITS = 16
LATENT_DIM = 10
EPOCHS = 10

# 实例化模型
model = DeepState(LSTM_UNITS, LATENT_DIM)

# 指定优化器
optimizer = tf.keras.optimizers.Adam()

# 定义训练步
def train_step(x, z):
    with tf.GradientTape() as tape:
        params, _ = model(x)
        _, _, loss_value = kalman_filtering(*params, z)
    gradients = tape.gradient(loss_value, model.trainable_variables)
    optimizer.apply_gradients(zip(gradients, model.trainable_variables))
    return loss_value.numpy()

# 数据处理（略）
# train_data = do_something()

# 训练
for epoch in range(EPOCHS):
    loss = []
    for x, z in train_data:
        loss.append(train_step(x, z))
    print('Epoch %d, Loss %.4f' % (epoch + 1, np.mean(loss))

为了验证代码是否有效，我们使用一个人工生成的时间序列进行训练，下图展示了这个序列的一部分数据点。

经过训练后用于预测，效果如下图所示，其中阴影部分表示 0.05 分位数 ~ 0.95 分位数的区间。

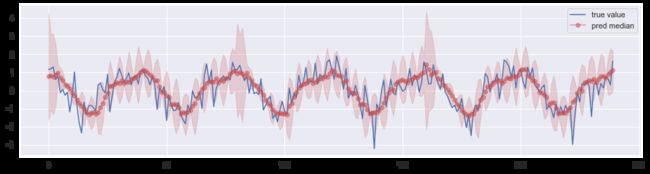
与 DeepAR 对比

• DeepAR 学习的是概率分布的参数，DeepState 学习的是状态空间模型的参数，因而 DeepState 具有更强的先验，在这个先验正确的前提下，理论上需要的训练数据应该更少一些。
• DeepAR 将当前时间步的目标值作为下一个时间步的输入，因而更容易受异常值的干扰，鲁棒性不如 DeepState。这种网络设计也导致了在预测阶段，每进行一轮采样，DeepAR 都要重新展开循环神经网络计算后验分布的参数。相比之下，DeepState 只需要使用网络计算一次状态空间模型的参数即可进行多轮采样²。
• DeepSate 基于线性高斯状态空间模型，很难推广到其它分布。DeepAR 则不存在这个问题，你可以根据数据特点选择合适的分布。

---

1. 这里使用的记号与原文略有不同。 ↩︎

2. 文章里是这样写的。但是得到状态空间模型的参数之后，每一轮采样也需要使用卡尔曼滤波算法递推计算，效率也并没有高到哪里去啊。 ↩︎