【论文阅读】HeCo:Self-supervised Heterogeneous Graph Neural Network with Co-contrastive Learning
具有协同对比学习的自监督异质图神经网络
- 摘要
- 1 准备工作
- 2 HeGo模型
-
- 2.1 节点特征转换
- 2.2 网络架构视角引导的编码器
- 2.3 元路径视角引导的编码器
- 2.4 视角掩蔽机制
- 2.5 协同对比优化( Collaboratively Contrastive Optimization)
- 2.6 模型扩展
-
- 2.6.1 HeCo_GAN
- 2.6.2 HeCo_MU
- 3 实验
-
- 3.1 实验设置
- 3.2 节点分类
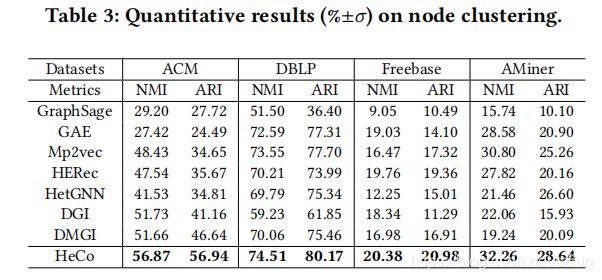
- 3.3 节点聚类
论文链接:https://arxiv.org/abs/2105.09111
代码链接:https://github.com/liun-online/HeCo
摘要
异质图神经网络(HGNNs)作为一种新兴技术,在处理异质信息网络(HIN)方面显示出了优越的能力。然而,大多数HGNNs采用半监督学习方式,这明显限制了其在实际应用中的广泛应用,因为在实际应用中标签通常很少。近年来,对比学习作为一种自监督学习方法,在没有标签的情况下显示出巨大的潜力。本文研究了HGNNs的自监督学习问题,提出了一种新的HGNNs协同对比学习机制HeCo。 与传统的只注重正负样本对比的对比学习不同,HeCo采用了跨视角(cross-view)对比机制。具体地说,本文提出了HIN的两个视角(网络架构和元路径视角)来学习节点嵌入,从而同时捕获局部和高阶结构。在此基础上,提出了跨视角对比学习的概念,并提出了一种视角掩蔽机制(view mask mechanism),从两种视角中提取正嵌入和负嵌入。这使得两个视角能够协作地相互监督,并最终学习到高阶节点嵌入。此外,本文还设计了两个HeCo扩展来产生高质量的harder negative samples,进一步提高了HeCo的性能。在各种真实网络上进行的大量实验表明,所提方法的性能优于现有技术。
1 准备工作
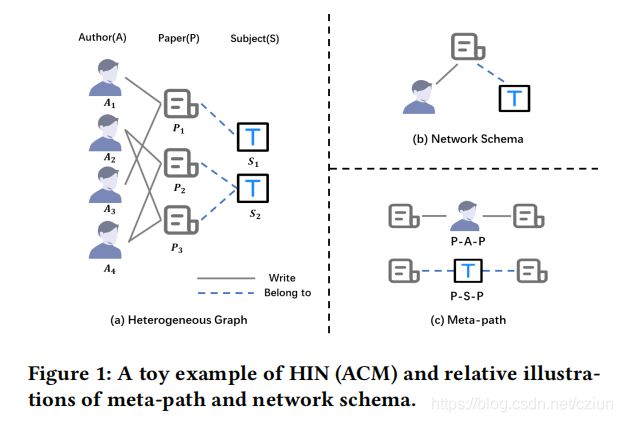
(1)异质信息网络(Heterogeneous Information Network)
HIN被定义为 G = { V , E , A , R , ϕ , ψ } \mathcal{G}=\{\mathcal{V},\mathcal{E},\mathcal{A},\mathcal{R},ϕ,ψ\} G={V,E,A,R,ϕ,ψ},其中, V \mathcal{V} V和 E \mathcal{E} E分别是节点集和边集,它们分别与节点映射函数 ϕ : V → A ϕ:\mathcal{V}→\mathcal{A} ϕ:V→A和边映射函数 ψ : E → R ψ:\mathcal{E}→\mathcal{R} ψ:E→R相关联, A \mathcal{A} A和 R \mathcal{R} R分别是节点类型集和边类型集, ∣ A + R ∣ > 2 |\mathcal{A}+\mathcal{R}|>2 ∣A+R∣>2。
(2)网络架构(Network Schema)
T G = ( A , R ) T_G=(\mathcal{A},\mathcal{R}) TG=(A,R),是HIN G \mathcal{G} G的一个元模板,是在 A \mathcal{A} A上定义的有向图,其边来自 R \mathcal{R} R。
网络架构用于描述不同节点之间的直接连接,它表示局部结构。
(3)元路径(Meta-path)
元路径 P \mathcal{P} P被定义为如下形式的路径, A 1 → R 1 A 2 → R 2 . . . → R l A l + 1 A_1\stackrel{R_1}{\rightarrow}A_2\stackrel{R_2}{\rightarrow}...\stackrel{R_l}{\rightarrow}A_{l+1} A1→R1A2→R2...→RlAl+1(缩写为 A 1 A 2 . . . A l + 1 A_1A_2...A_{l+1} A1A2...Al+1),它描述了节点类型 A 1 A_{1} A1和 A l + 1 A_{l+1} Al+1之间的复合关系 R = R 1 ◦ R 2 ◦ . . . ◦ R l R=R_1◦R_2◦...◦R_l R=R1◦R2◦...◦Rl, ◦ ◦ ◦表示复合运算符。
由于元路径是多重关系的组合,因此它包含了复杂的语义,这被认为是高阶结构。
2 HeGo模型
本节提出了HeCo,一种新的具有协同对比学习的异质图神经网络,整体架构如图2所示。该模型从网络架构视角和元路径视角编码节点,这完全捕获了HIN的结构。在编码过程中,还创造性地引入了视角掩蔽机制,它使这两个视角相互补充和监督。对于这两个特定视角的嵌入,我们对这两种视角使用了对比学习。考虑到节点间的高相关性,我们重新定义了HIN中一个节点的正样本,并特别设计了一种优化策略。

2.1 节点特征转换
首先,需要将所有类型节点的特征投影到一个公共的潜在向量空间中,如图2(a)所示。
具体来说,对于 ϕ ( i ) ϕ(i) ϕ(i)类型的节点 i i i,我们设计了一个特定类型的映射矩阵 W ϕ ( i ) W_{ϕ(i)} Wϕ(i)来将其特征 x i x_i xi转换到公共空间:
h i = σ ( W ϕ ( i ) ⋅ x i + b ϕ ( i ) ) (1) h_i=\sigma\big(W_{ϕ(i)}·x_i+b_{ϕ(i)}\big)\tag{1} hi=σ(Wϕ(i)⋅xi+bϕ(i))(1)
其中, h i ∈ R d × 1 h_i∈\mathbb{R}^{d×1} hi∈Rd×1是节点 i i i的投影特征, σ ( i ) \sigma(i) σ(i)是激活函数, b ϕ ( i ) b_{ϕ(i)} bϕ(i)表示向量偏差。
2.2 网络架构视角引导的编码器
现在我们的目标是学习在网络架构视角下节点 i i i的嵌入,如图2(b)所示。
根据网络架构,我们假设目标节点 i i i与 S S S种其他类型的节点 { Φ 1 , Φ 2 , . . . , Φ S } \{Φ_1,Φ_2,...,Φ_S\} {Φ1,Φ2,...,ΦS}相连接, 所以节点 i i i的 Φ m Φ_m Φm类型的邻居可被定义为 N i Φ m N_i^{Φ_m} NiΦm。对于节点 i i i,不同类型的邻居对其嵌入的贡献是不同的,相同类型的不同节点也是不同的。因此,我们在节点级和类型级使用注意机制,将来自其他类型邻居的消息分层聚合到目标节点 i i i。
具体地说,首先将节点级注意力应用于融合 Φ m Φ_m Φm类型的邻居【 h i Φ m ∈ R d × 1 h_i^{Φ_m}∈\mathbb{R}^{d×1} hiΦm∈Rd×1】:
h i Φ m = σ ( ∑ j ∈ N i Φ m α i , j Φ m ⋅ h j ) (2) h_i^{Φ_m}=\sigma\Bigg(\sum_{j∈N_i^{Φ_m}}\alpha_{i,j}^{Φ_m}·h_j\Bigg)\tag{2} hiΦm=σ(j∈NiΦm∑αi,jΦm⋅hj)(2)
其中, σ \sigma σ是激活函数, h j h_j hj是节点 j j j的投影特征, α i , j Φ m \alpha_{i,j}^{Φ_m} αi,jΦm表示从节点 j j j(类型为 Φ m Φ_m Φm)到节点 i i i的注意力值,计算如下:
α i , j Φ m = e x p ( L e a k y R e L U ( a Φ m T ⋅ [ h i ∣ ∣ h j ] ) ) ∑ l ∈ N i Φ m e x p ( L e a k y R e L U ( a Φ m T ⋅ [ h i ∣ ∣ h l ] ) ) (3) \alpha_{i,j}^{Φ_m}=\frac{exp\Big(LeakyReLU\Big(\pmb{a}_{Φ_m}^T·[h_i||h_j]\Big)\Big)}{\sum_{l∈N_i^{Φ_m}}exp\Big(LeakyReLU\Big(\pmb{a}_{Φ_m}^T·[h_i||h_l]\Big)\Big)}\tag{3} αi,jΦm=∑l∈NiΦmexp(LeakyReLU(aaaΦmT⋅[hi∣∣hl]))exp(LeakyReLU(aaaΦmT⋅[hi∣∣hj]))(3)
其中, a Φ m ∈ R 2 d × 1 \pmb{a}_{Φ_m}∈\mathbb{R}^{2d×1} aaaΦm∈R2d×1是 Φ m Φ_m Φm的节点级注意力向量, ∣ ∣ || ∣∣表示连接操作。
在实践中,我们并没有聚合 N i Φ m N_i^{Φ_m} NiΦm中所有邻居的信息,而是在每个epoch随机采样邻居的一部分。具体地说,如果 Φ m Φ_m Φm类型的邻居的数量超过了预定义的阈值 T Φ m T_{Φ_m} TΦm,我们将不可重复地选择 T Φ m T_{Φ_m} TΦm邻居作为 N i Φ m N_i^{Φ_m} NiΦm,否则就可以重复地选择 T Φ m T_{Φ_m} TΦm邻居。 这样,我们可以保证每个节点从邻居那里聚合到的信息的数量是相同的,并且在这个视角下可以促进每个epoch嵌入的多样性,这将使后续的对比任务更具挑战性。
一旦我们得到了所有类型的嵌入 { h i Φ 1 , . . . , h i Φ S } \{h_i^{Φ_1},...,h_i^{Φ_S}\} {hiΦ1,...,hiΦS}【 i i i为某一目标节点】,我们就利用类型级注意力将它们融合在一起,以得到网络架构视角下节点 i i i的最终嵌入 z i s c z_i^{sc} zisc。
首先,我们测量每种节点类型的权重:
w Φ m = 1 ∣ V ∣ ∑ i ∈ V a s c T ⋅ t a n h ( W s c h i Φ m + b s c ) , β Φ m = e x p ( w Φ m ) ∑ i = 1 S e x p ( w Φ i ) (4) w_{Φ_m}=\frac{1}{|V|}\sum_{i∈V}\pmb{a}_{sc}^T·tanh\big(\pmb{W}_{sc}h_i^{Φ_m}+\pmb{b}_{sc}\big),\\ \beta_{Φ_m}=\frac{exp(w_{Φ_m})}{\sum_{i=1}^Sexp(w_{Φ_i})}\tag{4} wΦm=∣V∣1i∈V∑aaascT⋅tanh(WWWschiΦm+bbbsc),βΦm=∑i=1Sexp(wΦi)exp(wΦm)(4)
其中, V V V是目标节点的集合, W s c ∈ R d × d \pmb{W}_{sc}∈\mathbb{R}^{d×d} WWWsc∈Rd×d和 b s c ∈ R d × 1 \pmb{b}_{sc}∈\mathbb{R}^{d×1} bbbsc∈Rd×1是可学习的参数, a s c \pmb{a}_{sc} aaasc表示类型级注意力向量。 β Φ m \beta_{Φ_m} βΦm被解释为 Φ m Φ_m Φm类型对目标节点 i i i的重要性。
对类型嵌入进行了加权和,以得到 z i s c z_i^{sc} zisc【 z i s c ∈ R d × 1 z_i^{sc}∈\mathbb{R}^{d×1} zisc∈Rd×1】:
z i s c = ∑ m = 1 S β Φ m ⋅ h i Φ m (5) z_i^{sc}=\sum_{m=1}^S\beta_{Φ_m}·h_i^{Φ_m}\tag{5} zisc=m=1∑SβΦm⋅hiΦm(5)
2.3 元路径视角引导的编码器
现在我们的目标是学习在高阶元路径结构视角下的节点嵌入,如图2(c)所示。
具体地说,给定一条来自 { P 1 , P 2 , . . . , P M } \{\mathcal{P}_1,\mathcal{P}_2,...,\mathcal{P}_M\} {P1,P2,...,PM}(都以节点 i i i开头)的元路径 P n \mathcal{P}_n Pn, 我们可以得到基于元路径的邻居 N i P n N_i^{\mathcal{P}_n} NiPn。例如,如图1(a)所示【 M = 2 M=2 M=2】, P 2 P2 P2是基于元路径 P A P PAP PAP的 P 3 P3 P3的邻居。
每条元路径表示一个语义相似性,我们应用元路径特定的GCN来编码此特征:
h i P n = 1 d i + 1 h i + ∑ j ∈ N i P n 1 ( d i + 1 ) ( d j + 1 ) h j (6) h_i^{\mathcal{P}_n}=\frac{1}{d_i+1}h_i+\sum_{j∈N_i^{\mathcal{P}_n}}\frac{1}{\sqrt{(d_i+1)(d_j+1)}}h_j\tag{6} hiPn=di+11hi+j∈NiPn∑(di+1)(dj+1)1hj(6)
其中, d i d_i di和 d j d_j dj是节点 i i i和 j j j的度, h i h_i hi和 h j h_j hj是它们的投影特征。
有 M M M条元路径,我们可以得到节点 i i i的 M M M个嵌入 { h i P 1 , . . . , h i P M } \{h_i^{\mathcal{P}_1},...,h_i^{\mathcal{P}_M}\} {hiP1,...,hiPM}。然后,我们利用语义级注意力,将它们融合起来,得到元路径视角下的最终嵌入:
z i m p = ∑ n = 1 M β P n ⋅ h i P n (7) z_i^{mp}=\sum_{n=1}^M\beta_{\mathcal{P}_n}·h_i^{\mathcal{P}_n}\tag{7} zimp=n=1∑MβPn⋅hiPn(7)
其中, β P n \beta_{\mathcal{P}_n} βPn权衡了元路径 P n \mathcal{P}_n Pn的重要性,其计算方法如下:
w P n = 1 ∣ V ∣ ∑ i ∈ V a m p T ⋅ t a n h ( W m p h i P n + b m p ) , β P n = e x p ( w P n ) ∑ i = 1 M e x p ( w P i ) (8) w_{\mathcal{P}_n}=\frac{1}{|V|}\sum_{i∈V}\pmb{a}_{mp}^T·tanh\big(\pmb{W}_{mp}h_i^{\mathcal{P}_n}+\pmb{b}_{mp}\big),\\ \beta_{\mathcal{P}_n}=\frac{exp(w_{\mathcal{P}_n})}{\sum_{i=1}^Mexp(w_{\mathcal{P}_i})}\tag{8} wPn=∣V∣1i∈V∑aaampT⋅tanh(WWWmphiPn+bbbmp),βPn=∑i=1Mexp(wPi)exp(wPn)(8)
其中, W m p ∈ R d × d \pmb{W}_{mp}∈\mathbb{R}^{d×d} WWWmp∈Rd×d和 b m p ∈ R d × 1 \pmb{b}_{mp}∈\mathbb{R}^{d×1} bbbmp∈Rd×1是可学习的参数, a m p \pmb{a}_{mp} aaamp表示语义级注意力向量。
2.4 视角掩蔽机制
在生成 z i s c z_i^{sc} zisc和 z i m p z_i^{mp} zimp的过程中,我们设计了一个视角掩蔽机制,它分别隐藏了网络架构和元路径视角的不同部分。图3为示意图,其中目标节点为 P 1 P_1 P1。
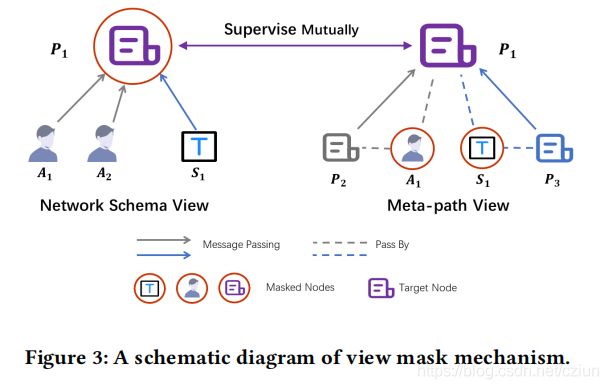
在网络架构编码的过程中, P 1 P_1 P1只将其邻居(包括作者 A 1 A_1 A1、 A 2 A_2 A2和主题 S 1 S_1 S1)聚合到 z 1 s c z_1^{sc} z1sc中,但来自它本身的消息被屏蔽了。
在元路径编码的过程中,消息只沿着元路径(例如 P A P PAP PAP, P S P PSP PSP)从 P 2 P_2 P2、 P 3 P_3 P3到目标节点 P 1 P_1 P1传递以生成 z 1 m p z_1^{mp} z1mp,而中间节点 A 1 A_1 A1和 S 1 S_1 S1的信息被丢弃。
因此,从这两个部分学习到的节点 P 1 P_1 P1的嵌入是相关的,但也是互补的。他们可以监督彼此的训练,这呈现出一种协作的趋势。
2.5 协同对比优化( Collaboratively Contrastive Optimization)
在从以上两个视角获得节点 i i i的 z i s c z_i^{sc} zisc和 z i m p z_i^{mp} zimp之后,我们将它们输入一个带有一个隐藏层的MLP,以将它们映射到计算对比损失的空间中:
z i s c _ p r o g = W ( 2 ) σ ( W ( 1 ) z i s c + b ( 1 ) ) + b ( 2 ) z i m p _ p r o g = W ( 2 ) σ ( W ( 1 ) z i m p + b ( 1 ) ) + b ( 2 ) (9) z_i^{sc}\_prog=W^{(2)}\sigma\Big(W^{(1)}z_i^{sc}+b^{(1)}\Big)+b^{(2)}\\ z_i^{mp}\_prog=W^{(2)}\sigma\Big(W^{(1)}z_i^{mp}+b^{(1)}\Big)+b^{(2)}\tag{9} zisc_prog=W(2)σ(W(1)zisc+b(1))+b(2)zimp_prog=W(2)σ(W(1)zimp+b(1))+b(2)(9)
其中, σ \sigma σ是ELU非线性激活函数。应该指出的是, { W ( 2 ) , W ( 1 ) , b ( 2 ) , b ( 1 ) } \{W^{(2)},W^{(1)},b^{(2)},b^{(1)}\} {W(2),W(1),b(2),b(1)}是由两个视角的嵌入共享的。
接下来,当计算对比损失时,我们需要定义HIN中的正样本和负样本。给定网络架构视角下的节点,我们可以简单地将其通过元路径视角学习的嵌入定义为正样本。然而,考虑到由于边的原因,这些节点通常是高度相关的,我们提出了一种新的正样本选择策略,即,如果两个节点由许多元路径连接,那么它们都是正样本,如图2(d)所示,其中论文之间的连接表示它们是彼此的正样本。这种策略的一个优点是,所选的正样本可以很好地反映目标节点的局部结构【?】。
对于节点 i i i和 j j j,我们首先定义一个函数 C i ( j ) \mathbb{C}_i(j) Ci(j)来计算连接这两个节点的元路径数:
C i ( j ) = ∑ n = 1 M 1 ( j ∈ N i P n ) (10) \mathbb{C}_i(j)=\sum_{n=1}^M\mathbb{1}\Big(j∈N_i^{\mathcal{P}_n}\Big)\tag{10} Ci(j)=n=1∑M1(j∈NiPn)(10)
然后,构造一个集合 S i = { j ∣ ( j ∈ V a n d C i ( j ) ≠ 0 } S_i=\{j|(j∈Vand\mathbb{C}_i(j)≠0\} Si={j∣(j∈VandCi(j)=0},并根据 C i ( j ) \mathbb{C}_i(j) Ci(j)的值降序排序。
接下来,设置一个阈值 T p o s T_{pos} Tpos,如果 ∣ S i ∣ > T p o s |S_i|>T_{pos} ∣Si∣>Tpos,我们从 S i S_i Si中选中前 T p o s T_{pos} Tpos个节点作为节点 i i i的正样本,记作 P i \mathbb{P}_i Pi,否则, S i S_i Si中的所有节点都被保留。我们自然地将所有剩余的节点【即 C i ( j ) = 0 \mathbb{C}_i(j)=0 Ci(j)=0】视为 i i i的的负样本,表示 N i \mathbb{N}_i Ni。
有了正样本集 P i \mathbb{P}_i Pi和负样本集 N i \mathbb{N}_i Ni,我们得到在网络架构视角下的对比损失:
L i s c = − l o g ∑ j ∈ P i e x p ( s i m ( z i s c _ p r o g , z j m p _ p r o g ) / τ ) ∑ k ∈ { P i ∪ N i } e x p ( s i m ( z i s c _ p r o g , z k m p _ p r o g ) / τ ) (11) \mathcal{L}_i^{sc}=-log\frac{\sum_{j∈\mathbb{P}_i}exp\Big(sim\Big(z_i^{sc}\_prog,z_j^{mp}\_prog\Big)/\tau\Big)}{\sum_{k∈\{\mathbb{P}_i∪\mathbb{N}_i\}}exp\Big(sim\Big(z_i^{sc}\_prog,z_k^{mp}\_prog\Big)/\tau\Big)}\tag{11} Lisc=−log∑k∈{Pi∪Ni}exp(sim(zisc_prog,zkmp_prog)/τ)∑j∈Piexp(sim(zisc_prog,zjmp_prog)/τ)(11)
其中, s i m ( u , v ) sim(u,v) sim(u,v)表示两个向量 u u u和 v v v之间的余弦相似度, τ \tau τ表示一个温度参数。
我们可以看到,与传统的对比损失(通常只关注公式(11)分子中的一个正对)不同,这里我们考虑多个正对。另外,请注意,对于一对中的两个节点,目标嵌入来自网络架构视角( z i s c _ p r o g z_i^{sc}\_prog zisc_prog),正样本和负样本的嵌入来自元路径视角( z k m p _ p r o g z_k^{mp}\_prog zkmp_prog)。这样,我们实现了跨视角自监督(the cross-view self-supervision)。
在元路径视角下的对比损失 L i m p \mathcal{L}_i^{mp} Limp 与 L i s c \mathcal{L}_i^{sc} Lisc相似,但不同的是,目标嵌入来自元路径视角,而正、负样本的嵌入来自网络架构视角。
总体目标如下:
J = 1 ∣ V ∣ ∑ i ∈ V [ λ ⋅ L i s c + ( 1 − λ ) ⋅ L i m p ] (12) \mathcal{J}=\frac{1}{|V|}\sum_{i∈V}\Big[\lambda·\mathcal{L}_i^{sc}+(1-\lambda)·\mathcal{L}_i^{mp}\Big]\tag{12} J=∣V∣1i∈V∑[λ⋅Lisc+(1−λ)⋅Limp](12)
其中, λ \lambda λ是一个用来平衡两个视角效果的系数。我们可以通过反向传播来优化该模型,并学习节点的嵌入。最后,我们使用 z m p z^{mp} zmp来执行下游任务,因为目标类型的节点显式地参与了 z m p z^{mp} zmp的生成。
2.6 模型扩展
众所周知,一个更难的负样本对于对比学习是非常重要的。因此,为了进一步提高HeCo的性能,我们提出了两种具有新的负样本生成策略的扩展模型。
2.6.1 HeCo_GAN
在HeCo中,负样本是原始HIN中的节点。在这里,我们从一个连续的高斯分布中采样额外的负样本。具体来说,HeCo_GAN由三个组件组成:HeCo、discriminator D D D 和 generator G G G。我们可以执行以下两个步骤,附录B中提供了更多细节:
(1)利用两个特定视角的嵌入来训练 D D D和 G G G。首先,我们训练 D D D识别两个视角的嵌入为正,从 G G G生成的嵌入为负。然后,我们训练 G G G生成高质量的样本以欺骗 D D D。上述两个步骤交替进行一些交互,使 D D D和 G G G进行训练。
(2)利用一个训练良好的 G G G来生成样本,这可以看作是新的高质量的负样本。然后,我们继续用新产生的负样本和原始的负样本训练HeCo。
2.6.2 HeCo_MU
MixUp通过添加任意两个样本来创建一个新样本,提高监督学习的效果。MoCHi将这一策略引入对比学习,后者mixes the hard negatives to make harder negatives。受到他们的启发,我们首次将这一策略带入HIN。
在计算公式(11)时,我们可以得到节点 i i i和 N i \mathbb{N}_i Ni中节点之间的余弦相似度,并按降序排序。然后,我们选择前 k k k个负样本作为the hardest negatives,并随机添加它们来创建新的 k k k个负样本,用于训练。值得一提的是,该方法没有可学习的参数,这是非常有效的。
3 实验
3.1 实验设置
本文将HeCo与三类Baselines进行了比较:
- 无监督同质方法: GraphSAGE、GAE、DGI
- 无监督异质方法:Mp2vec、HERec、HetGNN、DMGI
- 半监督异质方法:HAN