【机器学习】5. 线性模型 - 多分类 & LinearSVC
上一篇:Logistic回归&线性支持向量机
文章目录
- 多分类
- 实践
- 完整代码
多分类
许多线性分类模型只适用于二分类问题,不能轻易推广到多类别问题(除了Logistic回归)。将二分类算法推广到多分类算法的一种常见方法是“一对其余”(one-vs.-rest)方法。在“一对其余”方法中,对每个类别都学习一个二分类模型,将这个类别与所有其他类别尽量分开,这样就生成了与类别个数一样多的二分类模型。在测试点上运行所有二类分类器来进行预测。在对应类别上分数最高的分类器“胜出”,将这个类别标签返回作为预测结果。
每个类别都对应一个二类分类器,这样每个类别也都有一个系数(w)向量和一个截距(b)。下面给出的是分类置信方程,其结果中最大值对应的类别即为预测的类别标签:
w [ 0 ] ∗ x [ 0 ] + w [ 1 ] ∗ x [ 1 ] + ⋯ + w [ p ] ∗ x [ p ] + b w[0] * x[0] + w[1] * x[1] + \cdots + w[p] * x[p] + b w[0]∗x[0]+w[1]∗x[1]+⋯+w[p]∗x[p]+b
多分类Logistic回归背后的数学与“一对其余”方法稍有不同,但它也是对每个类别都有一个系数向量和一个截距,也使用了相同的预测方法。
实践
我们将“一对其余”方法应用在一个简单的三分类数据集上。我们用到了一个二维数据集,每个类别的数据都是从一个高斯分布中采样得出的:
from sklearn.datasets import make_blobs
import mglearn as mglearn
import matplotlib.pyplot as plt
X, y = make_blobs(random_state=42)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(["Class 0", "Class 1", "Class 2"])
plt.show()
 现在,在这个数据集上训练一个LinearSVC分类器:
现在,在这个数据集上训练一个LinearSVC分类器:
linear_svm = LinearSVC().fit(X, y)
print("Coefficient_shape: ", linear_svm.coef_.shape)
print("Interceprt_shape: ", linear_svm.intercept_.shape)
=============================================
Coefficient_shape: (3, 2)
Interceprt_shape: (3,)
我们看到,coef的形状是(3, 2),说明coef每行包含三个类别之一的系数向量,每列包含某个特征(这个数据集有2个特征)对应的系数值。现在intercept是一维数组,保存每个类别的截距。
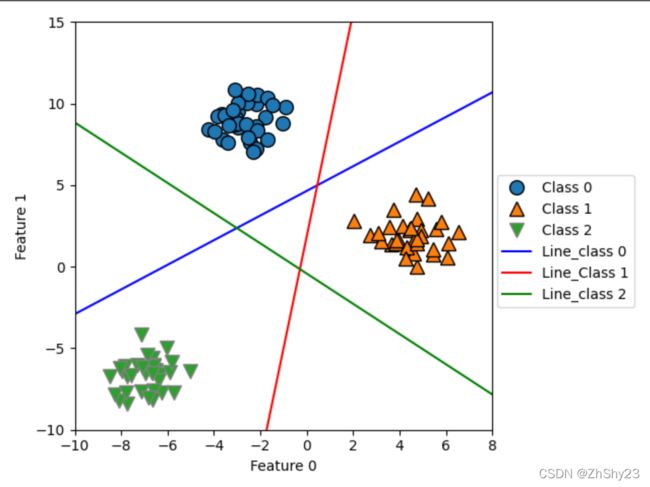
我们将这3个二类分类器给出的直线可视化:
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_, ['b', 'r', 'g']):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.ylim(-10, 15)
plt.xlim(-10, 8)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(
["Class 0", "Class 1", "Class 2",
"Line_class 0", "Line_Class 1", "Line_class 2"],
loc=(1.01, 0.3))
plt.show()
- 所有属于类别0的点都在与类别0对应的直线上方,这说明它们位于这个二类分类器属于“类别0”的那一侧。
- 属于类别0的点位于与类别2对应的直线上方,这说明它们被类别2的二类分类器划为“其余”。
- 属于类别0的点位于与类别1对应的直线左侧,这说明类别1的二元分类器将它们划为“其余”。
- 因此,这一区域的所有点都会被最终分类器划为类别0(类别0的分类器的分类置信方程的结果大于0,其他两个类别对应的结果都小于0)。
但图像中间的三角形区域属于哪一个类别呢,3个二类分类器都将这一区域内的点划为“其余”。这里的点应该划归到哪一个类别呢?答案是分类方程结果最大的那个类别,即最接近的那条线对应的类别。
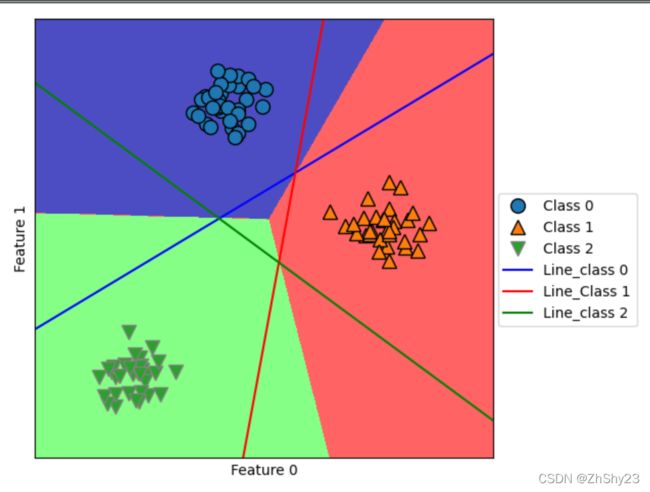
下面的例子给出了二维空间中所有区域的预测结果:
# 二维空间所有区域的预测结果
mglearn.plots.plot_2d_classification(linear_svm, X, fill=True, alpha=.7)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_, ['b', 'r', 'g']):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(
["Class 0", "Class 1", "Class 2",
"Line_class 0", "Line_Class 1", "Line_class 2"],
loc=(1.01, 0.3))
plt.show()
完整代码
from sklearn.datasets import make_blobs
from sklearn.svm import LinearSVC
import mglearn as mglearn
import matplotlib.pyplot as plt
import numpy as np
X, y = make_blobs(random_state=42)
# # 包含三个类别的二维玩具数据集
# mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
# plt.xlabel("Feature 0")
# plt.ylabel("Feature 1")
# plt.legend(["Class 0", "Class 1", "Class 2"])
# plt.show()
# 在数据集上训练一个LinearSVC分类器
linear_svm = LinearSVC().fit(X, y)
print("Coefficient_shape: ", linear_svm.coef_.shape)
print("Interceprt_shape: ", linear_svm.intercept_.shape)
# # 把这3个二类分类器给出的直线可视化
# mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
# line = np.linspace(-15, 15)
# for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_, ['b', 'r', 'g']):
# plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
# plt.ylim(-10, 15)
# plt.xlim(-10, 8)
# plt.xlabel("Feature 0")
# plt.ylabel("Feature 1")
# plt.legend(
# ["Class 0", "Class 1", "Class 2",
# "Line_class 0", "Line_Class 1", "Line_class 2"],
# loc=(1.01, 0.3))
# plt.show()
# 二维空间所有区域的预测结果
mglearn.plots.plot_2d_classification(linear_svm, X, fill=True, alpha=.7)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_, ['b', 'r', 'g']):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(
["Class 0", "Class 1", "Class 2",
"Line_class 0", "Line_Class 1", "Line_class 2"],
loc=(1.01, 0.3))
plt.show()