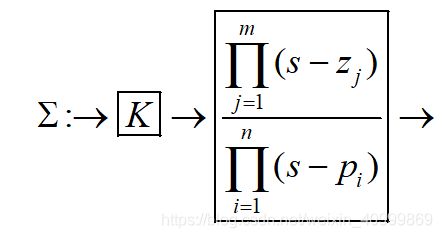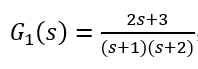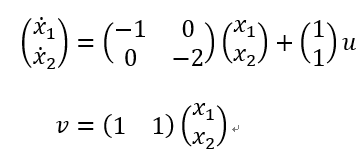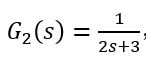基于零极点的最小实现和能控能观性讨论

摘 要

以零极点为出发点，讨论实现、最小实现与能控能观性的关系。通过将系统分为单输入单输出系统和多输入多输出系统，把多项式分解、零极点相消作为桥梁，搭建证明实现的最小实现与系统的能控能观性的关系。
关键词： 零极点 实现 最小实现 能控能观性 零极点相消

一、绪论

分析题目，我们需要从零极点出发，讨论实现、最小实现与能控能观性的关系。即想要通过零极点相消，讨论系统的实现时最小实现和系统能控能观的关系。因为单输入单输出系统（$SISO$）的情况和多输入多输出系统（$MIMO$）的情况不太相同，我们分别讨论$SISO$和$MIMO$系统。
对于单输入单输出的系统，我们首先明确，系统相关的基础概念，然后讨论系统中零极点相消和最小实现的关系，其次讨论系统的零极点相消和能控能观的关系，最后综合讨论得到系统的能控能观和最小实现的关系。
对于多输入多输出的系统，其中零极点的概念和零极点相消的概念比较复杂，我们先讨论相关概念，然后讨论系统中零极点相消和最小实现的关系，其次讨论系统的零极点相消和能控能观的关系，最后讨论得到系统的能控能观和最小实现的关系。
全文一共分为4节，除了第1节为绪论之外，其他各部分的内容安排如下：
（1）第2节，单输入单输出系统，我们以零极点相消为桥梁讨论最小实现和能控能观的关系并进行仿真；
（2）第3节，多输入多输出系统，我们以零极点相消为桥梁讨论最小实现和能控能观的关系并进行仿真；
（3）第4节，我们对上述的分析进行总结，得到整个文章分析的最终结论。

二、单输入单输出系统

2.1 概述

2.1.1 状态方程和实现

每个线性时不变系统都可以用输入-输出函数：$y(s)=G(s)u(s)$ 来描述，且这系统可以用状态方程描述为
$$\begin{array}{l}\dot{x}(t)=Ax(t)+Bu(t)\\ y(t)=Cx(t)+Du(t)\end{array}\text{\hspace{1em}(2.1)}$$
考虑$p$ 个输入$q$ 输出的$n$维状态方程，其中$A$,$B$’$C$ 和$D$ 分别为 和 的实常数矩阵[1]。
如果状态方程是已知的，那么传递函数阵可以求出$G(s)=C(sI-A{)}^{-1}B+D$，这样计算出来的传递函数阵是唯一的。相反，通过一个给定的传递函数求其对应的状态方程的问题，称为实现问题。
如果存在有限维的状态方程或者说$\{A,B,C,D\}$ 称为$G(s)$ 的一个实现。发散的线性时不变系统可以用传递函数描述，但是不能用有限维状态方程描述，所以不是所有的 都是可以实现的，如果$G(s)$ 可以实现，可实现的传递函数具有无穷多实现，但未必具有相同的维数。具有最小可能维数的实现称为“最小实现”[2]。

2.1.2 能控性和能观性

能控性

若对任意初始状态$x(0)=x_0$ ，和任意终止状态$x_1$ ，存在某个输入，在有限时间内能将状态从$x_0$ 转移到$x_1$ ，则称状态方程$(2.1)$或者矩阵$(A,B)$ “能控”。否则称方程$(2.1)$或者矩阵 $(A,B)$“不能控”

能观性

若对任意未知的初始状态$x(0)$ ，存在有限时间$t_1>0$ 使得已知$\left[0,t_1\right]$ 区间的输入$u$ 和输出$y$ 足以唯一地确定初始状态$x(0)$，则称状态空间方程$(2.1)$“能观”,否则，称该方程“不能观”

2.1.3 零极点及其相消的概念

下面我们给出了在单输入单输出系统中，零点、极点、零极点相消的概念。

零极点：

若一个$SISO$系统的传递函数为：
$$G(s)=\frac{Y(s)}{U(s)}=\frac{b_m{s}^m+b_{m-1}{s}^{m-1}+\cdots +b_{1}s+b_0}{a_n{s}^n+a_{n-1}{s}^{n-1}+\cdots +a_{1}s+a_0},a_n\ne 0\text{\hspace{1em}(2.2)}$$
那么，该系统的特征多项式（Characteristic Polynomial）为$D(s)$
$$D(s)=a_n{s}^n+a_{n-1}{s}^{n-1}+\cdots +a_{1}s+a_0\text{\hspace{1em}(2.3)}$$
系统的阶次（Degree）为特征多项式的阶次；
系统的零点（Zero）为分子多项式 $b_m{s}^m+b_{m-1}{s}^{m-1}+\cdots +b_{1}s+b_0$的根；
系统的极点（Pole）为特征多项式$a_n{s}^n+a_{n-1}{s}^{n-1}+\cdots +a_{1}s+a_0$ 的根。
传递函数的计算
$$G(s)=c(sI-A{)}^{-1}b=\frac{N(s)}{D(s)}=\frac{c.adj(sI-A)b}{\det (sI-A)}=K\frac{\prod _{j=1}^m(s-z_j)}{\prod _{i=1}^n(s-p_i)}\text{\hspace{1em}(2.4)}$$
以$N(s)$的根v 作为传递函数的零点，以$D(s)$的根$p_i$ 作为传递函数的极点。零点即当输入$u$ 为有限值，使输出 $y(s)$为零的那些$u$ 值，极点即当输入$u$ 为有限值，使输出$y(s)$ 为 的那些$s$值。

零极点相消：

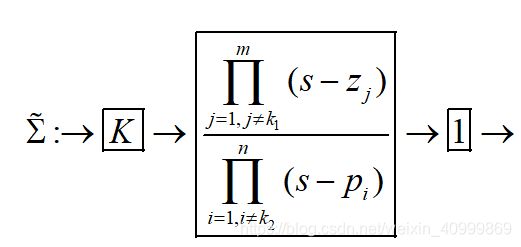
在上述的$SISO$系统中，有分子多项式$N(s)$的根，系统的零点$z_{k_1}$，特征多项式$D(s)$的根$p_{k_2}$，系统的极点 ，存在$z_{k_1}=p_{k_2}$ ，即
$$G(s)=K\frac{\prod _{j=1}^m(s-z_j)}{\prod _{i=1}^n(s-p_i)}=K\frac{\prod _{j=1,j\ne k_1}^m(s-z_j)}{\prod _{i=1,i\ne k_2}^n(s-p_i)}\text{\hspace{1em}(2.5)}$$
此时系统存在零极点相消。
注意：在$SISO$系统中分子多项式$N(s)$和特征多项式$D(s)$ 具有相同的根即系统存在零极点相消。这里我们得到，在$SISO$系统中，分子多项式$N(s)$和特征多项式$D(s)$具有相同的根是系统存在零极点相消的充要条件（这里概念在$MIMO$系统中有出入，在后面的分析中会用到）

互质分解：

多项式环上的互质分解

定义：$SISO$系统在多项式环上的分解$G(s)=\frac{N(s)}{D(s)}$中$N(s),D(s)$ 没有相同的零点（其中$N(s),D(s)$ 均为多项式，则称$N(s)$ 与 $D(s)$(在多项式环上)互质。
定理： $\left\{N(s),D(s)\right\}$互质当且仅当存在多项式 使得
$$X(s)N(s)+Y(s)D(s)=1\text{\hspace{1em}(2.6)}$$

稳定真有理分式集上的互质分解

定义：$SISO$系统在稳定真有理分式集上的分解$G(s)=\frac{N(s)}{D(s)}$，$N(s),D(s)$ 其中均为稳定真有理分式。若$N(s),D(s)$没有相同的不稳定零点（非最小相位零点），则称 $\left\{N(s),D(s)\right\}$（在稳定真有理分式集上）互质。
定理：$\left\{N(s),D(s)\right\}$互质当且仅当存在稳定真有理分式$X(s),Y(s)$使得
$$X(s)N(s)+Y(s)D(s)=1\text{\hspace{1em}(2.7)}$$

2.2 零极点相消和最小实现的关系

对于单输入单输出系统中的零极点相消和最小实现的关系讨论，我们的论文从以下两个命题出发：
命题一:单输入单输出系统中，系统的最小实现不存在零极点相消的情况
命题二:单输入单输出系统中，系统不存在零极点相消，该实现就是系统的最小实现。

2.2.1 命题一（充分性）

命题一:单输入单输出系统中，系统的最小实现不存在零极点相消。

反证法：

在单输入单输出系统，实现$\Sigma =(A,b,c)$是系统$G(s)$的最小实现，假设$G(s)$存在零极点相消，根据(2.4)可以得到

$$\begin{array}{l}N(s)=cadj(sI-A)b\\ D(s)=\det (sI-A)\end{array}\text{\hspace{1em}(2.8)}$$

根据$SISO$系统中零极点相消的概念，$G(s)$存在零极点相消， 比如$z_{k_1}=p_{k_2}$ ，那么$G(s)=\frac{N(s)}{D(s)}=K\frac{\prod _{j=1,j\ne k_1}^m(s-z_j)}{\prod _{i=1,i\ne k_2}^n(s-p_i)}\times \frac{(s-z_{k_1})}{(s-p_{k_2})}=K\frac{\prod _{j=1,j\ne k_1}^m(s-z_j)}{\prod _{i=1,i\ne k_2}^n(s-p_i)}=\tilde{G}(s)$ ，整个传递函数少了一个极点，系统降阶，可以找到一个更小维数的实现$\tilde{\Sigma }=(\tilde{A},\tilde{b},\tilde{c})$ 。因此系统的实现$\Sigma =(A,b,c)$不是系统的最小实现，和假设条件不矛盾，因此该命题正确。
从框图上可以表示为

图2-1 n维的系统的实现

图2-2 n-1维的系统的实现

2.2.2 命题二（必要性）

命题二:系统实现不存在零极点相消，该实现就是系统的最小实现。

反证法：

反设：系统实现的不存在零极点相消，假设$\Sigma (A,b,c)$ 不是$G(s)$ 的最小实现。则必然存在另一个系统 $\Sigma (\tilde{A},\tilde{b},\tilde{c})$

$$\begin{array}{l}\dot{\tilde{x}}=\tilde{A}\tilde{x}+\tilde{b}u\\ y=\tilde{c}\tilde{x}\end{array}$$
有更少的维数，使得：
$$\tilde{c}(sI-A{)}^{-1}\tilde{b}=c(sI-A{)}^{-1}b=G(s)$$
由于$\tilde{A}$的阶次比 低，于是多项式$\det (sI-\tilde{A})$的阶次低于$\det (sI-A)$的阶次，上式想成立，根据式(2.4) $N(s),D(s)$之间必然存在零极点对消。结论和条件矛盾，命题得证。

2.3 零极点相消和能控能观性的关系

对于单输入单输出系统中的零极点相消和能控能观性的关系讨论，我们的论文从以下两个命题出发：
命题三:单输入单输出系统，系统不存在零极点相消，则系统的实现能控且能观
命题四:单输入单输出系统，系统实现能控能观，则系统实现不存在零极点相消。

2.3.1 命题三（充分性）

命题三:单输入单输出系统，系统不存在零极点相消，则系统的实现是能控且能观。

反证法：

反设：单输入单输出系统，系统实现$\Sigma (A,b,c)$不存在零极点相消，假设系统是不是既能控且能观的，即系统是不能控或者不能观的。
第一种，假设系统是不能控的，按照能控性进行分解，
$$\begin{array}{l}\left[\begin{array}{c}{\dot{x}}_c\\ {\dot{x}}_{\bar{c}}\end{array}\right]=\left[\begin{array}{cc}{A}_c& A_{12}\\ 0& A_{\bar{c}}\end{array}\right]\left[\begin{array}{c}{x}_c\\ x_{\bar{c}}\end{array}\right]+\left[\begin{array}{c}{b}_c\\ 0\end{array}\right]u\\ y=\left[\begin{array}{cc}{c}_c& c_{\bar{c}}\end{array}\right]\left[\begin{array}{c}{x}_c\\ x_{\bar{c}}\end{array}\right]\end{array}$$

此时的传递函数为
$$\begin{array}{l}G(s)=c(sI-A{)}^{-1}b=\frac{c.adj(sI-A)b}{\det (sI-A)}=\frac{N(s)}{D(s)}\\ =c_c(sI-A_c{)}^{-1}{b}_c=\frac{c_{1}adj(sI-A_c)b_c}{\det (sI-A_c)}=\frac{N_c(s)}{D_c(s)}\end{array}\text{\hspace{1em}(2.9)}$$

在式$(2.9)$中， $D(s)$是 $n$次多项式，而$D_c(s)$ 是$n_1$ 次多项式，由于系统不可控，所以$n_1<n$ ，而$N(s),D(s)$ 不存在零极点相消，即互质，显然 $\frac{N(s)}{D(s)}\ne \frac{N_c(s)}{D{}_c(s)}$
出现矛盾，假设不成立
第二种，假设系统是不能观的，按照能观性分解，
$$\begin{array}{l}\left[\begin{array}{c}{\dot{x}}_o\\ {\dot{x}}_{\bar{o}}\end{array}\right]=\left[\begin{array}{cc}{A}_o& 0\\ A_{21}& A_{\bar{o}}\end{array}\right]\left[\begin{array}{c}{x}_o\\ x_{\bar{o}}\end{array}\right]+\left[\begin{array}{c}{b}_o\\ b_{\bar{o}}\end{array}\right]u\\ y=\left[\begin{array}{cc}{c}_o& 0\end{array}\right]\left[\begin{array}{c}{x}_c\\ x_{\bar{c}}\end{array}\right]\end{array}$$
此时的传递函数为
$$\begin{array}{l}G(s)=c(sI-A{)}^{-1}b=\frac{c.adj(sI-A)b}{\det (sI-A)}=\frac{N(s)}{M(s)}\\ =c_o(sI-A_o{)}^{-1}{b}_o=\frac{c_o.adj(sI-A_o)b_o}{\det (sI-A_o)}=\frac{N_o(s)}{D_o(s)}\end{array}\text{\hspace{1em}(2.10)}$$
式$(2.10)$中， 是 次多项式，而 $D_o(s)$是$n_2$次多项式，由于系统不可控，所以$n_2<n$，而$N(s),D(s)$不存在零极点相消，即互质，显然$\frac{N(s)}{D(s)}\ne \frac{N_o(s)}{D{}_o(s)}$
出现矛盾，假设不成立
两种情况都出现矛盾，假设不成立，命题得证。

2.3.2 命题四（必要性）

命题四:单输入单输出系统， $\Sigma =(A,b,c)$系统实现能控能观，则系统实现不存在零极点相消

反证法:

反设：单输入单输出系统， 系统实现能控能观，假设系统实现 $\Sigma =(A,b,c)$的传递函数$G(s)$存在零极点相消，即存在 使 ，结合$(2.8)$得到
$$\begin{array}{l}N(s_0)=c.adj(sI-A)b=0\\ D(s_0)=\det (sI-A)=0\end{array}\text{\hspace{1em}(2.11)}$$
$$(sI-A)(sI-A{)}^{-1}=(sI-A)\frac{adj(sI-A)}{\det (sI-A)}=I\text{\hspace{1em}(2.12)}$$
$$D(s)I=(sI-A)adj(sI-A)\text{\hspace{1em}(2.13)}$$
将$s=s_0$ 代入$(2.13)$，可得
$$Aadj(s_{0}I-A)=s_{0}adj(s_{0}I-A)\text{\hspace{1em}(2.14)}$$
式(2.14)左乘$c$ ，右乘$b$ ，得到
$$c.Aadj(s_{0}I-A)b=c.s_{0}adj(s_{0}I-A)b=s_{0}N(s_0)=0\text{\hspace{1em}(2.15)}$$
式(2.14)左乘$cA$，右乘$b$，得到，结合式$(2.15)$
$$c.A^{2}adj(s_{0}I-A)b=c.s_{0}Aadj(s_{0}I-A)b={s_0}^{2}N(s_0)=0\text{\hspace{1em}(2.16)}$$
由此类推可以得到
$$\begin{array}{l}N(s)=c.adj(s_{0}I-A)b=0\\ c.Aadj(s_{0}I-A)b=0\\ c.A^{2}adj(s_{0}I-A)b=0\\ ⋮\\ c.A^{n-1}adj(s_{0}I-A)b=0\end{array}\text{\hspace{1em}(2.17)}$$
将$(2.17)$中的式子组合起来，得到
$$\left[\begin{array}{c}c\\ cA\\ ⋮\\ c{A}^{n-1}\end{array}\right]adj(s_{0}I-A)b=0\text{\hspace{1em}(2.18)}$$
因为系统实现是能控能观的，上面的能观性判别矩阵是满秩，因此
$$adj(s_{0}I-A)b=0\text{\hspace{1em}(2.19)}$$
所以有
$$\begin{array}{l}adj(s_{0}I-A)b=\sum _{k=0}^{n-1}{p}_k(s_0)A^{k}b\\ \left[\begin{array}{cccc}b& Ab& \cdots & A^{n-1}b\end{array}\right]\left[\begin{array}{c}{p}_0(s_0)\\ p_1(s_0)\\ ⋮\\ p_{n-1}(s_0)\end{array}\right]=0\end{array}\text{\hspace{1em}(2.20)}$$
但因$p_{n-1}(s)\equiv 1$ ，故$\det \left[\begin{array}{cccc}b& Ab& \cdots & A^{n-1}b\end{array}\right]\equiv 0$ ， $\left[\begin{array}{cccc}b& Ab& \cdots & A^{n-1}b\end{array}\right]$能观判别阵不满秩，和系统完全能观矛盾，因此，证明命题正确。

2.4 零极点相消破坏系统的能控或能观性

为了更好的阐述零极点相消和能控性与能观性之间的关系，我们用串联系统去进行了进一步的解释和说明。
串联系统是由子系统按串联方式顺序联接的组合系统。现有两个线性时不变系统$S_1$与$S_2$，它们的传递函数分别为$G_1(s)$与$G_2(s)$，它们自身不存在零极点相消。将这两个系统作为子系统串联成为一个串联系统，其中子系统$S_1$的输入端加以输入$u$ ，$S_1$ 的输出端联接到子系统 $S_2$的输入端，$S_2$ 的输出规定为串联系统的输出$y$

图2-3 和 串联系统示意图

2.4.1串联系统不完全能控

若$G_1(s)$的零点与$G_2(s)$的极点形成相消，则串联系统不完全能控：
设$G_1(s)$的一个零点为$s=-p$，并简化 $G_2(s)=\frac{1}{s+p}$
$G_1(s)$ 的一个最小实现状态方程为，
$$\begin{array}{l}\dot{x}=Ax+bu\\ v=cx\end{array}\text{\hspace{1em}(2.21)}$$
则$G_2(s)$的最小实现状态方程为，

$$\begin{array}{l}\dot{z}=-pz+v\\ y=z\end{array}\text{\hspace{1em}(2.22)}$$
结合$(2.21)$和$(2.22)$所以它们串联后的系统的状态方程为，
$$\begin{array}{l}\left(\begin{array}{c}\dot{x}\\ \dot{z}\end{array}\right)=\left(\begin{array}{cc}A& 0\\ c& -p\end{array}\right)\left(\begin{array}{c}x\\ z\end{array}\right)+\left(\begin{array}{c}b\\ 0\end{array}\right)u\\ y=z\end{array}\text{\hspace{1em}(2.23)}$$
现讨论该串联系统的能控性，即考虑$\left[\lambda I-\bar{A}|\bar{b}\right]$的秩，已知$\lambda =-p$为 的$\bar{A}$特征值，则把$\lambda =-p$代入上式可得
$$\left[\left(\begin{array}{cc}-pI& 0\\ 0& -p\end{array}\right)-\left(\begin{array}{cc}A& 0\\ c& -p\end{array}\right)|\left(\begin{array}{c}b\\ 0\end{array}\right)\right]=\left[\begin{array}{ccc}-pI-A& 0& b\\ -c& 0& 0\end{array}\right]\text{\hspace{1em}(2.24)}$$
因为$s=-p$是$G_1(s)$的一个零点，所以$G_1(-p)=0$ ，即
$$c(-pI-A{)}^{-1}b=0\text{\hspace{1em}(2.25)}$$

记$(-pI-A{)}^{-1}b=m$ ，则有
$$\left(\begin{array}{cc}-pI-A& b\\ -c& 0\end{array}\right)\left(\begin{array}{c}m\\ -1\end{array}\right)=0\text{\hspace{1em}(2.26)}$$
因为$\left(\begin{array}{cc}-pI-A& b\\ -c& 0\end{array}\right)$为方阵，所以行秩等于列秩，可知$\left(\begin{array}{cc}-pI-A& b\\ -c& 0\end{array}\right)$非行满秩，所以串联系统不完全能控。

2.4.2串联系统不完全能观

若$G_1(s)$的极点与$G_2(s)$的零点形成相消，则串联系统不完全能观：
设$G_1(s)$的一个极点为$s=-z$，即满足：存在非零向量$n$ ，使$(-zI-A)n=0$，并简化$G_2(s)=\frac{1+z}{1-z}$ ，同理可以得到该子系统的最小实现的状态方程如下
$$\begin{array}{l}{\dot{x}}_z=z{x}_z-2zv\\ y=-x_z+v\end{array}\text{\hspace{1em}(2.27)}$$
所以串联系统的状态方程为：
$$\begin{array}{l}\left(\begin{array}{c}\dot{x}\\ {\dot{x}}_z\end{array}\right)=\left(\begin{array}{cc}A& 0\\ -2zc& -z\end{array}\right)\left(\begin{array}{c}x\\ x_z\end{array}\right)+\left(\begin{array}{c}b\\ 0\end{array}\right)u\\ y=\left(\begin{array}{cc}c& -1\end{array}\right)\left(\begin{array}{c}x\\ x_z\end{array}\right)\end{array}\text{\hspace{1em}(2.28)}$$
现考虑$\left(\begin{array}{c}-zI-\bar{A}\\ \bar{c}\end{array}\right)=\left(\begin{array}{cc}-zI-A& 0\\ 2zc& -2z\\ c& -1\end{array}\right)$的列秩，因为$s=-z$是$G_1(s)$的一个极点，所以$-zI-A=0$ ，且$c\ne 0$ ，所以可得$\left(\begin{array}{cc}-zI-A& 0\\ 2zc& -2z\\ c& -1\end{array}\right)$ 非列满秩，所以该串联系统不完全能观。
结论一：单输入单输出串联系统的能控性的充分条件： 极点不等于 传输零点；
结论二：单输入单输出串联系统的能观性的充分条件： 极点不等于 传输零点。

2.5 最小实现和能控能观性的关系

在单输入单输出系统中，上面$2.2$和$2.3$我们分别讨论了零极点相消和最小实现的关系与零极点相消和能控性能观性的关系。
根据命题一和命题三可以得到，在单输入单输出系统中，系统的实现是最小实现，系统不存在零极点相消，系统能控能观。根据命题二和命题四，系统的实现能控能观，系统的实现不存在零极点相消，那么系统的实现是最小实现。从上述的分析中我们得到了结论三 和结论四。对于最小实现和能控能观等价的直接证明，参照$3.4$节，这里不再重复赘述。

图2-4 $SISO$系统最小实现、零极点、能控能观关系图

结论三：在单输入单输出系统中，系统的实现是最小实现，系统的实现能控能观。
结论四：在单输入单输出系统中，系统的实现能控能观，系统的实现是最小实现。

2.6 仿真

2.6.1仿真（命题一、命题二、命题三、命题四）

针对$SISO$系统中的四个命题，命题一、命题二、命题三、命题四设计仿真。
接下来，我们对举例进行仿真，验证命题的证明。
例子：
对于两个实现$\left\{A_1,b_1,c_1\right\},\left\{A_2,b_2,c_2\right\}$ ，其中$A_1=-1,b_1=1,c_1=1$ ，$A_2=\left[\begin{array}{cc}-1& 0\\ 0& -2\end{array}\right],b_1=\left[\begin{array}{c}1\\ 1\end{array}\right],c_1=\left[\begin{array}{cc}1& 0\end{array}\right]$ ，计算传递函数，得
$$G_1(s)=c_1(sI-A_1{)}^{-1}{b}_1=\frac{1}{s+1}=G_2(s)=c_2(sI-A_2{)}^{-1}{b}_2=\frac{1}{(s+1)}$$

可以发现实现$\left\{A_1,b_1,c_1\right\}$没有零极点相消，实现 存在零极点相消，很容易观察到实现$\left\{A_1,b_1,c_1\right\}$是能控能观而且是系统的最小实现，实现 $\left\{A_2,b_2,c_2\right\}$能控不能观，实现$\left\{A_1,b_1,c_1\right\}$ 的阶次比实现$\left\{A_2,b_2,c_2\right\}$ 低，因此实现$\left\{A_2,b_2,c_2\right\}$ 不是最小实现。当然，我们也可以利用$MATLAB$函数$ctrb(A,B)$来判断能控性，函数$obsv(A,C)$判断能观性。能控能观的系统这符合命题一命题二命题三命题四是正确的证明结果。
我们对实现$\left\{A_1,b_1,c_1\right\},\left\{A_2,b_2,c_2\right\}$利用$MATLAB$的$Simulink$模块进行仿真，仿真的模块图如下所示：

图2-5 $SISO$系统仿真模型图

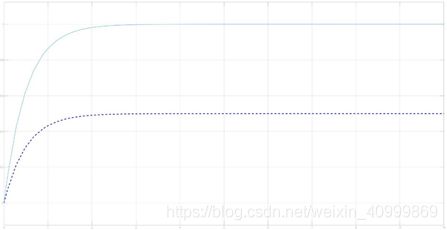
对于系统实现$\left\{A_1,b_1,c_1\right\}$ ，分别给出输入$u_1=1,u_1=2$，其状态$x_1$即输出$y_1$响应如下图：

图2-6 $SISO$例子$\left\{A_1,b_1,c_1\right\}$阶跃输出响应

其中实线$u_1=2$ 对应输出，虚线为$u_1=1$对应输出，从图2-6上我们可以看出零状态响应，不同的输入状态响应不同，说明系统能控，从输出$y_1$中可以观测到状态变量$x_1$，说明系统能观，从系统的结构上很容易看出，实现$\left\{A_1,b_1,c_1\right\}$不存在零极点相消，以及实现$\left\{A_1,b_1,c_1\right\}$是最小实现。
对于系统的实现$\left\{A_2,b_2,c_2\right\}$我们一样给定阶跃输入$u_2=1,u_2=2$，其状态$x_2$即输出$y_2$响应和状态$x_3$的输出如下图：

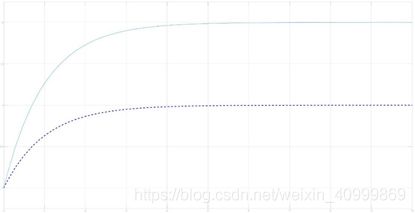
图2-7 $SISO$ $\left\{A_2,b_2,c_2\right\}$例子阶跃输入 输出响应

图2-8 $SISO$ $\left\{A_2,b_2,c_2\right\}$例子阶跃输入 响应

图2-7中实线是输入 $u_2=2$,$y_2$输出响应，虚线是输入 $u_2=1$,$y_2$输出响应。图2-8中实线是输入$u_2=2$, $x_3$响应，虚线是输入 $u_2=1$,$x_3$响应。
从图2-7中可以看出系统的输出$y_2$只和状态变量$x_2$有关，因此状态变量$x_3$不能观，改变输入，状态变量[{x_2},{x_3}]都会改变，状态变量$x_2,x{}_3$都能控，因此系统能控不能观，和上面分析的结果一样，侧面佐证了命题三和命题四是正确的。从图2-5我们分析实现$\left\{A_2,b_2,c_2\right\}$的模型图，很容易看出，系统存在阶次更低的实现，即模型图2-5圈出部分，实现$\left\{A_2,b_2,c_2\right\}$不是最小实现，也和上面的分析结果一样，侧面佐证了命题一和命题二是正确的。

2.6.2仿真（串联系统）

接下来我们对串联系统里的结论一结论二进行仿真。

仿真一（结论一）：

其最小实现的状态方程为：

其最小实现的状态方程为：

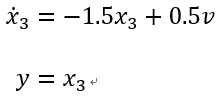
按上述串联方式串联后的系统的状态方程为：

系统的特征值为

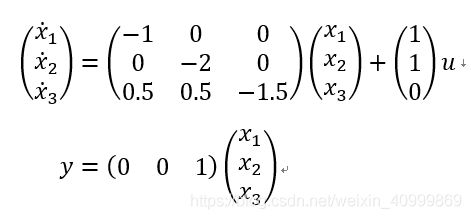
计算能观矩阵的秩
，该系统完全能观
可以计算得$rank([{\lambda }_{3}I-A|b])=2<3$，即$x_3$不能控，下面是仿真的系统图：

图2-9 串联系统仿真系统图（系统不能控）

对该系统以此输入1（左）和10（右）的阶跃信号，零状态响应曲
线如下：

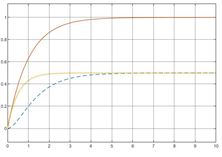
图2-10a零状态响应曲线

图2-10b零状态响应曲线

从两个阶跃可以看出，$x_3=x_1-x_2$，因此不能通过改变控制信号，使每个状态到达任意位置，因此系统不能控，满足所提出的结论。

仿真二（结论二）：

将仿真一中的两个子系统的串联顺序交换，可得到新的串联系统，该系统的状态方程如下：

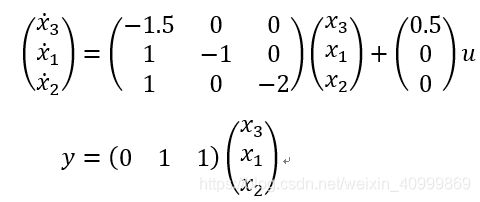
计算能控性矩阵的秩$rank([(b,Ab,A^{2}b)])=3$，该系统完全能控

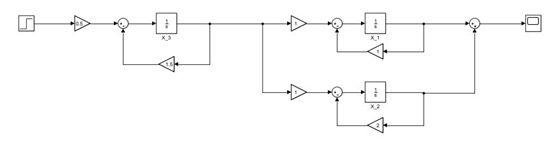
图2-11 串联系统仿真系统图（系统不能观）

可以计算得$rank\left(\begin{array}{c}{\lambda }_{3}I-A\\ c\end{array}\right)=2<3$，即$x_3$不能观，仿真结构图如下：
计算该系统的零输入响应：
$$y(t)=c{e}^{A}tx(0)=x_1(0)e^{(}-t)+x_2(0)e^{(}-2t)+2x_3(0)(e^{(}-t)-e^{(}-2t))$$
所以当$x_1(0):x_2(0):x_3(0)=-2:2:1$时，系统的零输入响应恒为零，如下图：

图2-12 系统的零输入响应

当仿真系统的三个状态按上述比例进行设置时，系统的输出都恒为零，所以可以判定该系统不完全能观。

三、多输入多输出系统

3.1 概述

状态方程、实现、能控性、能观性等概念都已经在2.1节中介绍，这里不再重复，下面介绍$MIMO$系统中零极点、零极点相消、传递函数的分解等概念。
$p$个输入$q$个输出的线性时不变系统可表示为真有理分式矩阵 $G(s)$
$$G(s)=\left[\begin{array}{ccc}{g}_{11}(s)& \cdots & g_{1p}(s)\\ ⋮& & ⋮\\ g_{q1}(s)& \cdots & g_{qp}(s)\end{array}\right]$$状态方程(2.1)可以写为：
$$\left[\begin{array}{c}\dot{x}\\ y\end{array}\right]=\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]\left[\begin{array}{c}x\\ u\end{array}\right]$$速记符号为$$G=\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]$$

传递函数$G(s)$是一个关于复杂的参数$s$的函数$$G(s)=C(sI-A{)}^{-1}B+D\text{\hspace{1em}(3.1)}$$ 为了更好地进行零极点的讨论和方便后面的推到证明，我们首先需要明确概念传递函数的阶次和阶次的概念。

3.1.1 阶次和秩

阶次

$MIMO$传递函数$G(s)$的阶次$\mathrm{deg}G(s)$:所有子式的最小公分母的阶次。
例：传递函数$G(s)=\left[\begin{array}{cc}\frac{1}{s+2}& \frac{1}{s+2}\\ \frac{1}{s+2}& \frac{1}{s+2}\end{array}\right]$ 。其一阶子式为$\frac{1}{s+2}$，二阶子式是$\det G(s)$，它们的最大公分母为$s+1$。因此，系统的阶次为1阶。

传递函数矩阵$G(s)$的秩：

$G(s)$最大可以获得的秩称为$G(s)$的秩，若记为$r_G$，则$$r_G=\underset{s\in \mathrm{C}}{\max }rankG(s)\text{\hspace{1em}(3.2)}$$例：$G(s)=\left[\begin{array}{cc}\frac{s+1}{s+2}& 0\\ 0& \frac{s+2}{s+3}\end{array}\right]$ ， $rankG(-1)=1,rankG(1)=2$这是$G(s)$可能取得的最大的秩，因此$G(s)$的秩为2

3.1.2 零极点及其相消

零点

在多变量系统中，我们先明确传递函数矩阵$G(s)$的零点$s_0$，使得$G(s)$在$s=s_0$时降秩。
若存$s$平面上的点$z$ 使得$G(z)$的秩小于$G(s)$的秩，则称 $z$为$G(s)$的零点；由于$G(z)$是降秩的，则存在向量$v,w$，使得$G(z)v=0$（或$w^{T}G(z)=0$，我们称$v$为零点$z$的右方向向量， $w$为零点$z$的左方向向量[3]。

极点

有状态空间方向的系统极点$p_i\in C$是特征值${\lambda }_i(A)$，$i=1,\cdots ,n_x$，极点特征多项式$\varphi (s)$为：$\varphi (s)=\det (sI-A)=\prod _{i=1}^{n_x}(s-p_i)$ ，因此极点就是特征方程的根
$$\varphi (s)=\det (sI-A)=0$$

系统$G$在$s=p$的平均增益$G(p)$在输入输出方向上是无限的，这是定义极点输入输出方向的基础。

极点的输入输出方向

如果$s=p\in C$是$G(s)$的极点，进而存在输出方向$y_p\in C^l$和输入方向$u_p\in C^m$ ，方向上$s=p$时增益无限大[3]。

$MIMO$系统的多项式分解：

$$G(s)=\left[\begin{array}{ccc}{g}_{11}(s)& \cdots & g_{1p}(s)\\ ⋮& & ⋮\\ g_{q1}(s)& \cdots & g_{qp}(s)\end{array}\right]=N(s)M^{-1}(s)={\tilde{M}}^{-1}(s)\tilde{N}(s)\text{\hspace{1em}(3.3)}$$其中$N(s)M^{-1}(s)$为右分解,${\tilde{M}}^{-1}(s)\tilde{N}(s)$ 为左分解。

零极点相消：

根据式子$(3.3)$的分解得到，
$$G(s)=N(s)M^{-1}(s)=N(s)E(s)E(s{)}^{-1}{M}^{-1}(s)=\left[N(s)E(s)\right]{\left[M(s)E(s)\right]}^{-1}\text{\hspace{1em}(3.4)}$$
对传递函数进行左分解时，通过判断$\tilde{M}(s)$和 $\tilde{N}(s)$的零点的左方向是否相同，来判断是否存在零极点相消。即$\tilde{M}(s)$ 和 $\tilde{N}(s)$的零点的左方向相同，存在零极点相消，反之，则不存在零极点相消。
对传递函数进行右分解时，通过判断$M(s)$和$N(s)$的零点的右方向是否相同，来判断是否存在零极点相消。即$M(s)$ 和$N(s)$ 的零点的右方向相同，存在零极点相消，反之，则不存在零极点相消。
对传递函数进行右分解时，若$\lambda$是$M(s)$的根$v$是极点$s=\lambda$的右方向，$(v,V)$单位正交阵，则$M(s)$包含一个一阶因子$M_0(s)$，满足$M_0(\lambda )v=0$，得
$$\begin{array}{l}M(s)=\hat{M}(s)M_0(s)\\ M_0(s)=\left(\begin{array}{cc}s-\lambda & 0\\ 0& I\end{array}\right)\left(\begin{array}{c}{v}^T\\ V\end{array}\right)\end{array}\text{\hspace{1em}(3.5)}$$式子$(3.5)$中$\left(\begin{array}{c}{v}^T\\ V^T\end{array}\right)\left(\begin{array}{cc}v& V\end{array}\right)=I$，式子$(3.5)$左右取行列式，得到$$\det M(s)=\det \hat{M}(s)\det M_0(s)=s-\lambda \text{\hspace{1em}(3.6)}$$带入极点的定义，得
$$M(\lambda )v={M(s)|}_{s=\lambda }v={\hat{M}(s)|}_{s=\lambda }\left(\begin{array}{cc}0& 0\\ 0& I\end{array}\right)\left(\begin{array}{c}{v}^T\\ V\end{array}\right)v={\hat{M}(s)|}_{s=\lambda }\left(\begin{array}{cc}0& 0\\ 0& I\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)=0\text{\hspace{1em}(3.7)}$$

同理，$N(s)=\hat{N}(s)N_0(s),N_0(s)=\left[\begin{array}{cc}s-\lambda & 0\\ 0& I\end{array}\right]\left[\begin{array}{c}{w}^T\\ W\end{array}\right]$ ，其中$(w,W)$ 是单位正交阵。
当$M(s)$的根与$N(s)$的根有相同的方向时，存在零极点相消，$$\begin{array}{l}G(s)=N(s)M^{-1}(s)\\ =\hat{N}(s)N_0(s)M_0^{-1}(s){\hat{M}}^{-1}(s)\\ =\hat{N}(s)\left[\begin{array}{cc}s-\lambda & 0\\ 0& I\end{array}\right]\left[\begin{array}{c}{w}^T\\ W\end{array}\right](\left[\begin{array}{cc}s-\lambda & 0\\ 0& I\end{array}\right]\left[\begin{array}{c}{v}^T\\ V\end{array}\right]{)}^{-1}{\hat{M}}^{-1}(s)\\ =\hat{N}(s){\hat{M}}^{-1}(s)\end{array}\text{\hspace{1em}(3.8)}$$
类似地，对传递函数进行左分解时，若$\lambda$是$\tilde{M}(s)$的根， $v$是极点$s=\lambda$的左方向， $(v,V)$单位正交阵，则$\tilde{M}(s)$包含一个一阶因子$M_0(s)$，满足$v^T{M}_0(\lambda )=0$。
$$\begin{array}{l}\tilde{M}(s)=M_0(s)\hat{M}(s)\\ M_0(s)={\left(\begin{array}{c}{v}^T\\ V\end{array}\right)}^T\left(\begin{array}{cc}s-\lambda & 0\\ 0& I\end{array}\right)\end{array}\text{\hspace{1em}(3.9)}$$
式子$(3.9)$中$\left(\begin{array}{c}{v}^T\\ V^T\end{array}\right)\left(\begin{array}{cc}v& V\end{array}\right)=I$ ，式子$(3.9)$左右取行列式，得到
$$\det \tilde{M}(s)=\det \hat{M}(s)\det M_0(s)=s-\lambda \text{\hspace{1em}(3.10)}$$
带入极点的定义，得$$v^{T}M(\lambda )=v$$