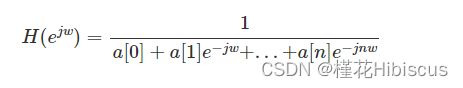MNE实例分析：基于AR模型的时域白化处理

2023/1/20-2023/1/22脑机接口学习内容一览：

        这一篇博客里，主要针对《EEG 脑电信号分析方法及其应用》by 李颖洁 中的对于AR模型内容的不理解，结合mne库中的示例代码Temporal whitening with AR model，通过翻译和代码复现做一点具体的分析与学习。

前言：

         在这一篇博客里，我们通过AR模型对信号进行拟合与时域白化。

        这里有两个需要注意的点。

        1.什么是AR模型？

        2.对信号时域的白化操作有什么意义？

---

概念理解：

1.AR模型

        模型法就是通过模型来对数据进行拟合，如果模型能够很好地描述数据，就可以用于进行谱估计和特征提取。拟合的意义在于明确数据的变化趋势。对于AR模型来说，它使用前面信号的线性加权来表示后面的信号。根据脑电信号的非平稳性，显然自适应模型对拟合数据有着更好的效果。

        在mne中，使用mne.time_frequency.fit_iir_model_raw函数来实现拟合AR模型到原始数据，并创建相应的IIR过滤器。计算得到的滤波器拟合所有选取通道的数据，频率响应由标准IIR公式给出，这个式子符合前面给出的线性加权规律:

 2.白化操作

        参考【1】、【2】。

        白化操作，是将各向异性的特征(每一列是一个特征，每一行是一条数据)，转化为各向同性，大家(不同特征)在一个尺度下。“白化”的概念也就是把一个不满足上述特性的信号变成具有上述特性的信号，同时能够保留原信号的某些特征。

        如果对输入数据进行白化处理，就能降低数据特征之间的相关度，也就是特征分离，那么不同数据所蕴含的信息之间的重复性就会降低，网络的训练效率就会提高。

        那么标题中的所谓“基于AR模型的时域白化处理”也就稍微容易理解一点了，接下来我们将会从代码角度来深入这个问题。

---

代码示例：

首先引入头文件和提取raw，以及一些基本的预处理操作：

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt

import mne
from mne.time_frequency import fit_iir_model_raw
from mne.datasets import sample


data_path = sample.data_path()
meg_path = data_path / 'MEG' / 'sample'
raw_fname = meg_path / 'sample_audvis_raw.fif'
proj_fname = meg_path / 'sample_audvis_ecg-proj.fif'

raw = mne.io.read_raw_fif(raw_fname)
proj = mne.read_proj(proj_fname)    # 从fif文件中读取投影
raw.add_proj(proj)                  # 将ecg投影加入raw中用于去除ecg伪影
raw.info['bads'] = ['MEG 2443', 'EEG 053']  # 标记坏通道

# 设置pick条件：选择梯度计，排除坏通道
picks = mne.pick_types(raw.info, meg='grad', exclude='bads')

在raw数据中计算AR模型  fit_iir_model_raw函数返回的a, b分别是根据0号频道计算得出的分母滤波系数和分子滤波系数

order = 5  # 定义模型顺序,这里的意思可能是在前面取的过去输入输出的个数
# 这一步对pick的操作不是很懂，picks只取了第一个通道
print('one', picks)
picks = picks[:1]
print('two', picks)

'''
在raw数据中计算AR模型
fit_iir_model_raw函数返回的a, b分别是根据0号频道计算得出的分母滤波系数和分子滤波系数
'''
b, a = fit_iir_model_raw(raw, order=order, picks=picks, tmin=60, tmax=180)
d, times = raw[0, 10000:20000]  # 只看0号频道从10000到20000的采样点
print(d.shape)
print(a)
d = d.ravel()  # 创建平面向量
innovation = signal.convolve(d, a, 'valid')     # 对d和a数组进行卷积操作
d_ = signal.lfilter(b, a, innovation)  # 重新生成信号
d_ = np.r_[d_[0] * np.ones(order), d_]  # 假样本保持信号长度

画图

plt.close('all')
plt.figure()
plt.plot(d[:100], label='signal')
plt.plot(d_[:100], label='regenerated signal')
plt.legend()

plt.figure()
plt.psd(d, Fs=raw.info['sfreq'], NFFT=2048)
plt.psd(innovation, Fs=raw.info['sfreq'], NFFT=2048)
plt.psd(d_, Fs=raw.info['sfreq'], NFFT=2048, linestyle='--')
plt.legend(('Signal', 'Innovation', 'Regenerated signal'))
plt.show()

---

 结果分析：

         从第一幅图可以看出AR模型拟合的数据基本与源信号重合。

         这一张图表现的是白化处理的效果。

---

参考文献：

【1】whitening白化处理的意义

【2】Whiten process——数据的白化处理