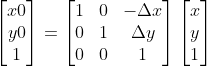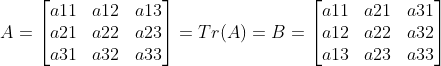opencv图像处理学习（五）——坐标映射,平移,缩放,旋转

1.坐标映射

图像的坐标映射是涌过原图像与目标图像之间建立一种映射关系，这种映射关系有两种：一种是计算原图像任意像素在映射后图像的坐标位置，另一种是计算变换后图像任意像素反映在原图像的位置。

opencv提供重映射的相关操作，对于一个图像的一个位置的像素通过映射关系转换到另一图像的制定位置。对于原图像f（x，y），目标图像为g（x，y），映射关系为T，则有下式：

其相关函数是：

void remap(InputArray src,OutputArray img,InputArray map1,InputArray map2,int interpolation,int borderMode=BORDER_CONSTANT,const Scalar&borderValue=Scalar());

其中map1表示（x，y）点的坐标或x坐标，可以是CV_16SC2等类型，map2表示y坐标，也可以是CV_16UC1，也可以选择不用，interpolation表示插值方法，BorderMode表示边界插值类型，BorderValue表示插值数值。

e.g:

Mat Image =imread("……");

Mat result(Image.size(),Image.type());

Mat x (Image.size(),Image.type());

Mat y (Image.size(),Image.type());

int rows = Image.rows;

int cols = Image.cols;

for(int j = 0;j(j,i) = cols - i;

     y.at(j,i) = rows - j;

 }

}

remap(Image,result,x,y,CV_INTER_LINEAR,cv::BORDER_CONSTANT,cv::scalar(0,0,0));

2.平移

图像平移的操作是将图像所有像素坐标进行水平或垂直方向移动，也就是所有像素点按照给定的偏移量在水平方向上沿x轴、垂直方向为y轴上移动。在保证图像大小变化与图像大小不变的条件下，平移变换分为两种：一种类型保证图像平移的完整信息，第二种原始信息部分可能丢失。平移变换公式如下：

对于平移操作，其变换矩阵均为左乘。

对于原始图像，其正交变换矩阵为：

对于目标图像，其逆变换矩阵为：

对4x4图像矩阵向右移x轴一个单位，向下平移y轴一个单位，若移动后图像的大小保持不变，多余部分填充为白色时满足：

平移操作在opencv中需要自己写函数，下面给出一个参考代码

e.g:cv::Mat  imageTranslation(cv::Mat & srcImage,int xOffset,int yOffset)

{

  int nRows = srcImage.rows;

  int nCols = srcImage.cols;

  cv::Mat resultImage(srcImage.size(),srcImage.type());

 //遍历图像

for(int i = 0;i=0&&y>=0&&x(i,j) = srcImage.ptr(y)[x];

            //typedef vector Vec3b

            //这里Ptr<>模板类就是一种智能指针，也可以理解成一个指针，或者是一个指针类，可以防止内存泄漏等问题，比普通指针好用。PS：后面再开一个C++补充知识的，不是系统学习C++，我先现学一步。

        }

  }

}

return resultImage;

}

3.缩放

图像缩放是指将图像的尺寸变小或变大的过程，也就是减少或增加源图像数据的像素个数。图像缩放在一定程度上会造成信息的丢失。缩放分为两种，一种是基于等间隔提取图像缩放，另一种是基于区域子块提取

<1>基于等间隔提取图像缩放

等间隔提取图像是通过对原图像进行均匀采样来完成的。对于源图像数据f（x，y），其分辨率为MxN，如果将其分辨率改成为mxn，其宽度缩放因子kx=M/m,高度缩放因子ky=N/n。若kx=ky，则等比例缩放，若不等于，则会造成图像变形扭曲现象。f（x，y）变换成g（x',y'）矩阵为右乘，关系式如下：

Ps：这里缩放变换矩阵右乘是因为像素矩阵是1行3列，平移是3行1列，也就是说像素矩阵决定了变换矩阵的左乘还是右乘。

<2>基于区域子块提取图像缩放

区域子块提取缩放是通过对源图像进行区域子块划分，然后提取子块中像素值作为采样像素以构成新图像来实现的。

提取子块区域值常用方法有计算子块像素的中值与计算子块像素的均值。对源图像进行区域划分同样也有不同方法，常用的方法是根据缩放因子等比例提取子块与自适应因子提取子块。

假设图像f（x，y）的分辨率是8x8，图像g（x',y'）的分辨率是2x2，其区域子块提取方式如下：

在opencv中，缩放的函数为：

Resize（const cvArr* src，cvArr *dst，Size dsize， double fx， double fy，int inertpolation = CV_INTER_LINEAR）

其中第一个参数是输入图像；第二个参数是输出图像；第三个是输出图像尺寸，如果为0，则由dsize=Size(round(fx*src.cols),round(fy*src,rows))计算得出，第四个为水平缩放因子，第五个为垂直缩放因子；第六个是插值方式，OpenCV提供了5种插值方法：最邻近、双线性、基于像素区域、立方插值及兰索斯插值（后期文章会单独讲），其中双线性插值与最邻近插值的时间复杂度相对较低。

4.旋转

图像旋转是指图像按照某个位置转动一定角度的过程，旋转中图像仍保持着原始尺寸。图像旋转后图像的水平对称轴、垂直对称轴及中心坐标原点可能都会发生变化。图像中的坐标系由x轴水平方向向右，y轴竖直方向向下构成。设图像旋转中心为（cx，cy），源图像数据坐标（x，y）,旋转后目标图像坐标为（x'，y'）,首先需要将坐标原点由图像左上角变换到旋转中心，旋转坐标转换矩阵形式为:

在极坐标情况下顺时针选择，根据坐标转换可得旋转转换为：

将其转换为图像矩阵表达式为：

opencv中旋转（逆时针方向）的函数是Mat resultImage=angelRotate（Mat srcImage，int angel）；

图像翻转是图像旋转的特例，翻转是指沿图像中心选择90度或180度的过程，opencv中提供了transpose与filp函数进行矩阵转置变换，可以将图像进行水平或垂直翻转。

transpose函数的作用是矩阵转置，也就是f（i，j）=g（j，i）：

e.g:Mat A=imread("……");

Mat B；

transpose(A,B);

filp函数的作用是沿轴翻转，其函数如下

flip(Mat A,Mat B,int flags);

其中A表示源矩阵，B表示目标矩阵，flags为关键参数，当其大于0时沿y轴翻转，等于0是x轴，小于0表示同时。