r语言 计算模型的rmse_R语言pec包深度验证Cox模型
01
研究背景
在cox回归中,如何利用已经构建好的预测模型预测单个患者的生存概率呢?R中的pec包中predictSurvProb()函数可以利用cph()拟合的模型计算验证集中患者在不同时间节点的生存概率。其次该包还能在验证集中计算不同时间点C-index指数,绘制成图,比较验证集在不同模型中的C-index,通过交叉验证评估不同模型的区分度,除此以外该包还能将2个模型的校准度曲线绘制在同一个坐标系中,非常好用的包。
02
案例研究
本文数据采用一份肿瘤生存资料数据集,收集了449例癌症患者的生存资料,包含患者年龄、性别、、吸烟史、生化检验、生存时间、生存状态等45个变量。本文利用Lasso回归做变量选择,构建cox预测模型,通过pec包验证区分度和校准度。
03
R代码及解读
##加载包 明确每个包的作用library(pec) ##验证模型library(rms) ##拟合生存分析模型library(survival) ##生存分析包library(glmnet) ##Lasso回归包第一步,数据整理。
##调用数据,数据格式与普通的spss中格式一样,一行代表一条观测, dtvartypevartype###transdata 自编小函数 转化数据结构transData for (i in 1:length(vartype)) { if(vartype[i]==0){df[,i] else if(vartype[i]!=0){df[,i] } return(df)}dfstr(df) ## 查看数据结构dt 第二步:Lasso回归做变量选择
##筛选变量前,首先将自变量数据(因子变量)转变成矩阵(matrix)x.factors #将矩阵的因子变量与其它定量边量合并成数据框,定义了自变量。x=as.matrix(data.frame(x.factors,dt[,c(21:44)]))#设置应变量,生存时间和生存状态(生存数据)y #调用glmnet包中的glmnet函数,注意family那里一定要制定是“cox”,如果是做logistic需要换成"binomial"。fit plot(fit,label=T)plot(fit,xvar="lambda",label=T) ##见图一#主要在做交叉验证,lassofitcv plot(fitcv) ## 见图2print(fitcv) ## 1个标准差对应变量少,选此收缩系数## Lambda Measure SE Nonzero## min 0.02632 11.96 0.2057 21## 1se 0.11661 12.15 0.1779 5coef(fitcv, s="lambda.1se") ## 查看入选变量,后面有数字的为入选变量##此处关于Lasso的解释可看公众号之前推的文章。## 47 x 1 sparse Matrix of class "dgCMatrix"## 1## dt.oper.name2 . ## dt.relapse1 0.4400809## dt.group.tumor.dia2 . ## dt.group.tumor.dia3 . ## dt.sex1 . ## dt.age.group2 . ## dt.region2 . ## dt.smoking1 . ## dt.group.hepth.medical.his1 . ## dt.group.ther.be.op1 . ## dt.BCLC2 0.1037029## dt.BCLC3 -0.1612514## dt.group.melt.time2 . ## dt.group.melt.time3 . ## dt.tumor.single.double2 0.1797434## dt.group.tumor.num2 . ## dt.group.tumor.num3 . ## dt.group.tumor.size2 . ## dt.group.tumor.location2 . ## dt.AFP2 . ## dt.AFP3 0.2251439## dt.CEA2 . ## dt.CA1992 . ## inpatient.days . ## differ1.WBC . ## differ1.N. . ## differ1.HGB . ## differ1.PLT . ## differ1.Alb . ## differ1.ALT . ## differ1.AST . ## differ1.TB . ## differ1.DB . ## differ1.Scr . ## differ1.PT . ## differ1.APTT . ## differ1.INR . ## differ2.WBC . ## differ2.N . ## differ2.HGB . ## differ2.PLT . ## differ2.Alb . ## differ2.ALT . ## differ2.AST . ## differ2.TB . ## differ2.DB . ## differ2.Scr第三步:随机拆分数据集为训练集和测试集
set.seed(1234)x % runif() ## 随机生成449个生成从0到1区间范围内的服从正态分布的随机数dt % arrange(sample)###随机排列数据集样本###拆分数据集train test 第四步:构建模型
#### Lasso回归筛选出来 变量 #### relapse BCLC tumor.single.double AFP### cox1 为全模型cox1 ### cox2 诶筛选变量搭建的模型cox2 第五步:预测生存概率
### 设置预测生存概率的时间点,根据模型预测患者1年,3年和5年的生存概率。t survprob head(survprob)### 365 1095 1825### 225 0.9837627 0.9448162 0.8785664### 226 0.9677175 0.8924489 0.7714278### 227 0.9522695 0.8440149 0.6792448### 228 0.9409147 0.8096285 0.6177702### 229 0.7941521 0.4496941 0.1615871### 230 0.8204438 0.5034604 0.2090600第六步:模型区分度对比和验证
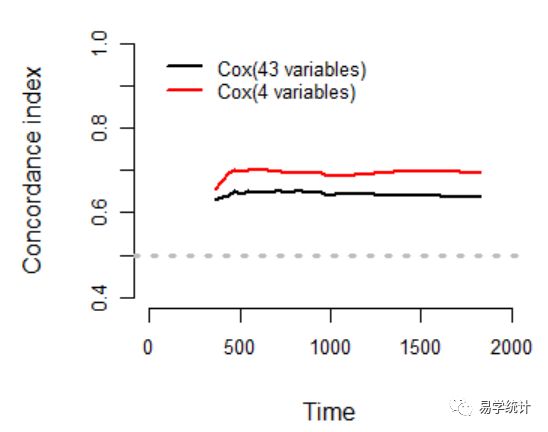
## eval.times 输入评价模型区分能力的时间点向量,缺少的话系统认为是最大生存时间## 此时相当于单个时间点评估,同之前文章中求的模型concordance## 这个就是优于rms的一个点,可以对每个时间点比较。c_index formula=Surv(live.time,outcome==1)~., data=test, eval.times=seq(365,5*365,36.5))## 设置画图参数##mar 以数值向量表示的边界大小,顺序为“下、左、上、右”,单位为英分*。##默认值为c(5, 4, 4, 2) + 0.1##mgp 设定标题、坐标轴名称、坐标轴距图形边框的距离。默认值为c(3,1,0),##其中第一个值影响的是标题## cex.axis 坐标轴刻度放大倍数## cex.main 标题的放大倍数## legend.x,legend.y 图例位置的横坐标和纵坐标## legend.cex 图例文字大小par(mgp=c(3.1,0.8,0),mar=c(5,5,3,1),cex.axis=0.8,cex.main=0.8)plot(c_index,xlim = c(0,2000),legend.x=1,legend.y=1,legend.cex=0.8)上图表明cox2模型的区分度略好于cox1模型,可以进一步做交叉验证的方式比较两个模型的区分度。在验证集中,同时采用bootstrap重抽样法进行交叉验证。
##splitMethod 拆分方法 ="bootcv"表示采用重抽样方法##B表示重抽样次数c_index formula=Surv(live.time,outcome==1)~., data=test, eval.times=seq(365,5*365,36.5), splitMethod="bootcv", B=1000)plot(c_index,xlim = c(0,2000),legend.x=1,legend.y=1,legend.cex=0.8)上图表明含有4个变量的模型区分度要好于全模型,模型更加简洁,也从侧面印证前面的Lasso变量筛选是合适的。
第七步:校准曲线绘制
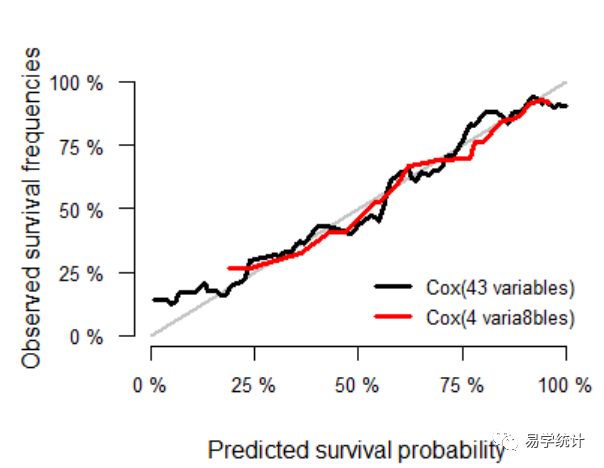
##该函数和rms包中的calibrate()函数原理一致。calPolt1 "Cox(4 varia8bles)"=cox2), time=3*365,#设置想要观察的时间点,同理可以绘制其他时间点的曲线 data=test,legend.x=0.5, legend.y=0.3,legend.cex=0.8) print(calPolt1) ##查看内容同理在验证集中,同时采用bootstrap重抽样法进行交叉验证,提高结果稳定性。
calPolt2 "Cox(4 variables)"=cox2), time=3*365,#设置想要观察的时间点 data=test,legend.x=0.5, legend.y=0.3,legend.cex=0.8, splitMethod = "BootCv", B=1000)上图表明含有4个变量的模型校准度要好于全模型。
04
总结
1.关于Lasso回归的原理和函数的参数说明,请查看本公众号之前的文章(如何进行高维变量筛选和特征选择(一)?Lasso回归)。
2.cindex()函数可以评估每个时间点的区分能力,并且可以将2个模型的区分度画到一个坐标里面,这优于rms包的区分度计算。calplot()函数可以画出模型的校准曲线,且可以将多个模型画到同一坐标系。
3.Bootstrap是用小样本估计总体值的一种非参数方法,其核心思想是
①采用重抽样的方法,从原始样本中有放回的抽取一定数量的样本,②根据抽到的样本计算给定的统计量T,③重复抽样N次(一般1000次),得到N个统计量T,④计算N个统计量T的样本方差,得到统计量方差。例如,要进行1000次bootstrap,求平均值的置信区间,可以对每个伪样本计算平均值。这样就获得了1000个平均值。对1000个平均值的分位数进行计算, 即可获得置信区间。已经证明,在初始样本足够大的情况下,bootstrap抽样能够无偏得接近总体的分布。
4.Bootstrap重抽样和交叉验证的区别。其相同之处,都是在数据集较小的时候常用的方法,提高结果的稳定性。不同之处,其一,两者的目的不同。CV主要用于模型选择上,例如KNN中选多大的K,使得估计的误差比较小。而Bootstrap主要用来看选定的模型的不确定性,例如参数的标准差多大。其二,两者的resample方法不同。在k fold CV中,把原始数据集分成k等分(各等分之间没交集),每一次验证中,把其中一份作为验证集,剩余的作为训练集。而在Bootstrap中,并不区分验证集和训练集,并且在resample中,是可放回抽样的,即同一个样本可以重复出现。
05
参考文献
方积乾等. 卫生统计学. 人民卫生出版社。
http://www.360doc.com/content/19/0915/20/47588191_861250278.shtml
http://www.360doc.com/content/19/0915/16/47588191_861207584.shtml
https://www.zhihu.com/question/19906494
作者介绍:医疗大数据统计分析师,擅长R语言。
欢迎各位在后台留言,恳请斧正!
更多阅读:
如何进行高维变量筛选和特征选择(一)?Lasso回归
R语言实现Cox模型校准度曲线绘制
![]()