对Finger-vein biometric identification using convolutional neural network的理解以及扩展应用

读了这篇关于手指静脉识别的文章，想利用其中的思想，用于手掌静脉识别问题当中。在这里列出文中的一些思路和自己的联想扩展。

首先是文章的理论背景。LeCun等人提出了一种称为Lenet-5的知名CNN架构。在手写识别问题中应用的Lenet-5CNN，包括了执行卷积与降采样操作交替的七个层。

第一层卷积涉及有卷积核的输入，基本上作为提取输入样本的显著特征的边缘检测器。在这种情况下，尺寸为5*5的核由包含产生模糊（低通滤波器），锐化（高通滤波器）或者边缘增强效果的加权系数组成。

第二层执行降采样，即对非重叠的局部平均，在此情况下窗口大小为2*2。作用是降低了来自前一层的特征图的分辨率。增加了抵抗平移、旋转和缩放中的小失真的鲁棒性。

这种框架的最后两层是充当分类器的MLP。

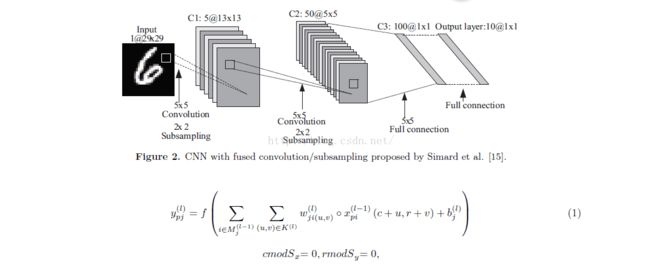
本文提出的CNN架构是基于Simard等人的工作，其中卷积和降采样层融合成一层。如图2所示，该融合显著地将CNN中层的总数从7减少到4。Simard等人的CNN也被用于手写识别，并且实现了比Lenet-5更高的精度。融合卷积和降采样层可以由等式（1）描述。

公式的解释略去，此处不谈论细节实现。在后面的学习中再深入实现。

建议的方法：本文所提出的静脉生物识别系统的开发在两个部分讨论：预处理阶段和CNN设计。设计的图像采集、图像预处理和分割···等暂不讨论。

本文中捕获的原始图像是240*320像素的，然后将图像裁剪成70*130的尺寸，将原点设置在手指图像的中心像素处（这样尽管样本中的小手指不对准，中心像素对于所有的样本是固定的）。裁剪的尺寸大小几乎覆盖整个手指，我们执行裁剪，也减少了本地动态阈值处理的过程中所消耗的时间，这也将随后应用与分割阶段。将图像大小调整为55*67像素，减少一些信息内容，以便于后续的NN训练。此图像的大小对要选择的卷积内核的大小有着显著的影响。

本文通过两种情况来评估所提出的系统的鲁棒性，即通过分割（使用局部动态阈值，这里称为情况A）和不执行分割的情况（参考作为情况B）。具体见文中。这里不作为重点，重点是谈论使用的网络结构。

重点：建议的CNN架构

如前所述，所提出的CNN架构基于由Simard等人首先提出的融合卷积和降采样层组成的设计。

图6给出了用于手指静脉生物识别所提出的CNN架构：CNN由四层（C1，C2，C3，C4卷积层不包括输入层）组成。我们将这种架构称为5-13-50模型，意味着在层C1，C2和C3中分别有5、13和50特征图。

层4，即输出层固定在50个神经元，因为要分类的目标类别数目是50个受试者。

我们来关注一下在MLP分类器的最后两层的1*1神经元，每个层同时执行提取特征和降维处理，每层的特征图的大小遵循以下等式：原文（4）

为了破坏对称性并且减少自由参量的数量，我们不对C1-C2应用完全连接方案，我们连接C1中的某些特征图以在C2中生成新的特征图。

我们通过交叉验证技术检查五种连接类型（如表2），以找到最佳连接方案（交叉验证是一种流行的经验方法来估计NN的最佳模型和参数），在交叉验证中，训练集被分为两个不相交的集合：一个集合包含要训练的样本，另一个集合用于验证。

通过10折的交叉验证，我们的5-13-50模型的每一层都使用这些方法进行测试。

最佳模型通过选择最低验证错误的模型来确定，在我们的CNN设计中应用的最终连接方案在表3中给出。

我们选择双曲正切作为激活函数，如文中的公式（5）。

在这个CNN设计中，分类是基于the winner-takes-all规则，输出神经元彼此竞争，其中只有最大输出值的神经元被确定为获胜者。

这种方法更为简单和有效，因为只需要在这些输出神经元中找到最大输出值的操作，以便确定模式的类别。取代了在生物特征识别过程中常用的相似性度量识别方法。

为了更快的收敛性能，随机的随机对角Levenberg-Marquardt学习算法来训练NN。关于这种学习算法在后续详细写。均值平方误差被用作成本函数。

环境：该系统运行在2.5GHz Intel i5-3210M四核处理器，8GB RAM，使用ubuntu Linux操作系统，算法在C中实现，并且用Matlab 9.0做预处理。

交叉验证结果只是对NN性能的估计，NN的实际性能必须在测试样本（100个样本）上进行评估。通过分类的准确性来度量网络的性能。

讨论最合适的归一化和权重初始化的方法：各给出了几种，分组匹配确定。

接下来问题的关键是谈论随机对角Levenberg-Marquardt算法来确保更快的收敛。