基于K均值(KMeans)与EM法估计高斯混合模型(GMM)参数的图像分割matlab程序
前些天已经写过KMeans图像分割和高斯混合模型EM法图像分割的文章,今天写一写KMeans与EM法估计高斯混合模型参数相结合的文章。具体操作流程见下图所示(摘自Szeliski的《计算机视觉——算法与应用》中文版p223)(图片上传后旋转了,大概CSDN默认图像宽度不小于高度吧,大家可自行下载观看,有知道解决办法的小伙伴可以在评论区分享一下经验):
下面给出本人实现的matlab程序:
function [sg,normMuDiff]=KMeansEMSeg(img,k,Mu,eps)
normMuDiff=[];
m=size(img,1);
n=size(img,2);
c=size(img,3);
N=m*n;
img=double(img);
M=reshape(img,m*n,c);
% index=randperm(m*n);
% Mu=M(index(1:k),:);
flag=1;
pc=rand(1,k); pc=pc/sum(pc); % 各类总的概率归一化
Cov=repmat(eye(c),1,1,k)*30^2; %k个聚类的协方差
C=zeros(c,c,k); %协方差的逆矩阵
snormCov=zeros(1,k);%各聚类协方差范数平方根
w=zeros(m*n,k); %各像素点对于聚类的权重矩阵
Label=zeros(m*n,1);
iter=1;
figure;
while flag
old_Mu=Mu;
%--------------------E步------------------------------%
%估计每个点属于各类的概率
for j=1:k
% Cov(:,:,j)=Cov(:,:,j)+5^2;
C(:,:,j) =inv(Cov(:,:,j));%使用Mahalanobis距离(即马氏距离)度量
snormCov(j)=sqrt(norm(Cov(:,:,j)));
end
for i=1:N
dis=zeros(k,1);
for j=1:k
dis(j)=(M(i,:)-Mu(j,:))*C(:,:,j)*(M(i,:)-Mu(j,:))';
w(i,j)=pc(j)*exp(-dis(j)/2)/snormCov(j);
w(i,j)=max(w(i,j),10^-5); %概率截断阈值化,防止矩阵奇异造成计算误差骤增第一重保险(阈值建议取值10^-5~10^-4)
end
end
w=w./repmat(sum(w,2),1,k); %各点关于各类的概率归一化
%--------------------M步----------------------------%
%估计各类均值、协方差及该类总的概率
for j=1:k
pc(j)=sum(w(:,j));
Mu(j,:)=w(:,j)'*M/pc(j); %估计均值
D=M-repmat(Mu(j,:),N,1);
W=sparse(1:N,1:N,w(:,j),N,N); %构造稀疏权重矩阵
Cov(:,:,j)=(1/pc(j))*D'*W*D;
%绝对值截断阈值化,防止矩阵奇异的第二重保险,该例建议阈值取值范围1~10(也可去掉第二重保险)
temp=Cov(:,:,j);
index=find(abs(temp)<10);
temp(index)=sign(temp(index)).*10;
Cov(:,:,j)=temp;
end
pc=pc/sum(pc); %各类总的概率归一化
%记录误差值,达到设定误差限停止循环
normDiff=norm(old_Mu-Mu);
if normDiff脚本文件:
clear all;close all;clc;
img=imread('onion.png');
% 初始值是在图中黄、绿、红、白、紫部分随机取一点得到的RGB值
Mu=[255 220 50;...
115 124 31;...
216 50 39;...
247 215 185;...
75 45 75];
[sg,normMuDiff]=KMeansEMSeg(img,5,Mu,1);
figure,imshow(mat2gray(sg));
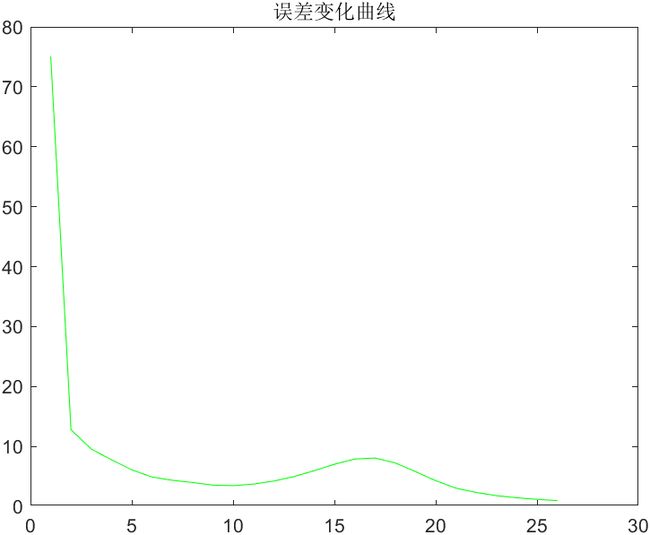
figure,plot(1:length(normMuDiff),normMuDiff,'g-');
title('误差变化曲线');输入原图:
迭代过程分割结果:
最终结果:
误差变化曲线:
如果严格按照书中步骤去做,GMM中作为马氏距离度量矩阵(的逆矩阵)的协方差矩阵有可能出现矩阵奇异的情况,这种情况的处理对结果的影响很大,处理得不好甚至会导致运算不收敛。限制每个像素点归属于各类的概率下限可以极大程度上改善这种情况。如果结果还不理想,可以对协方差元素的绝对值也进行阈值截断。注意,两重保护中的阈值选取都不能过大,否则会导致残差不断波动而最终不收敛或者最终收敛到一个非预期结果。由此可见,协方差矩阵奇异的情况处理起来还是要非常小心的。