RL策略梯度方法之(十一):proximal policy optimization (PPO)
本专栏按照 https://lilianweng.github.io/lil-log/2018/04/08/policy-gradient-algorithms.html 顺序进行总结 。
文章目录
- 原理解析
-
- 理论部分推导
-
- 1. PG算法回顾
- 2. PG方法的小tip
- 3. PPO算法原理简介
- 4. 特殊说明
- 算法实现
-
- 总体流程
- 代码实现
近端策略优化算法
P P O \color{red}PPO PPO :[ paper | code ]
原理解析
PPO在原目标函数的基础上添加了KL divergence 部分,用来表示两个分布之前的差别,差别越大则该值越大。那么施加在目标函数上的惩罚也就越大,因此要尽量使得两个分布之间的差距小,才能保证较大的目标函数。
TRPO 与 PPO 之间的差别在于它使用了 KL divergence(KL散度) 作为约束,即没有放到式子里,而是当做了一个额外的约束式子,这就使得TRPO的计算非常困难,因此较少使用。
理论部分推导
1. PG算法回顾
Actor对于一个特定的任务,都有自己的一个策略 π π π,策略 π π π 通常用一个神经网络表示,其参数为 θ θ θ 。从一个特定的状态state出发,一直到任务的结束,被称为一个完整的eposide,在每一步,我们都能获得一个奖励 r r r,一个完整的任务所获得的最终奖励被称为 R R R。这样,一个有 T T T 个时刻的eposide,Actor 不断与环境交互,形成如下的序列 τ τ τ:

这样一个序列 τ τ τ 是不确定的,因为Actor在不同state下所采取的action可能是不同的,一个序列 τ τ τ 发生的概率为:

序列 τ τ τ 所获得的奖励为每个阶段所得到的奖励的和,称为 R ( τ ) R(τ) R(τ) 。因此,在Actor的策略为 π π π 的情况下,所能获得的期望奖励为:
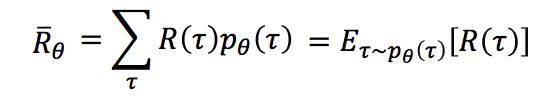
而我们的期望是调整Actor的策略 π π π,使得期望奖励最大化,于是我们有了策略梯度的方法,既然我们的期望函数已经有了,我们只要使用梯度提升的方法更新我们的网络参数 θ θ θ(即更新策略 π π π)就好了,所以问题的重点变为了求参数的梯度。梯度的求解过程如下:

上面的过程中,我们首先利用 log 函数求导的特点进行转化,随后用 N N N 次采样的平均值来近似期望,最后,我们将 p θ p_θ pθ 展开,将与 θ θ θ 无关的项去掉,即得到了最终的结果。
所以,一个PG方法的完整过程如下:
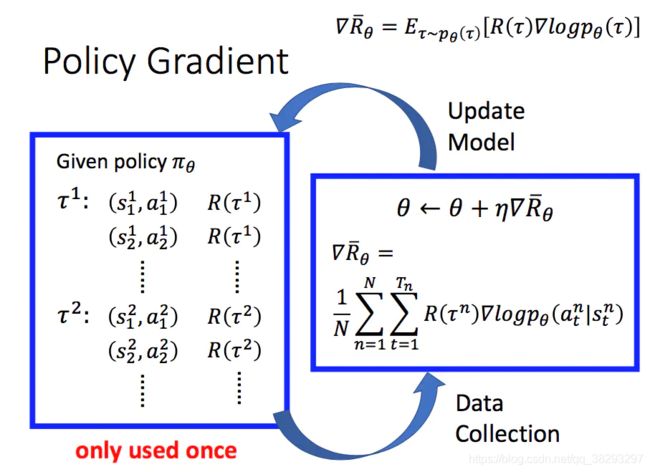
我们首先采集数据,然后基于前面得到的梯度提升的式子更新参数,随后再根据更新后的策略再采集数据,再更新参数,如此循环进行。注意到图中的大红字only used once,因为在更新参数后,我们的策略已经变了,而先前的数据是基于更新参数前的策略得到的。
2. PG方法的小tip
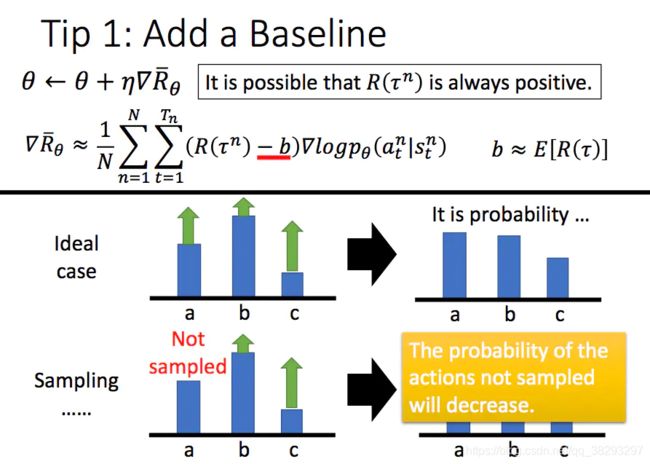
增加一个基线
通过上面的介绍你可能发现了,PG方法在更新策略时,基本思想就是增加reward大的动作出现的概率,减小reward小的策略出现的概率。假设现在有一种情况,我们的reward在无论何时都是正的,对于没有采样到的动作,它的reward是0。因此,如果一个比较好的动作没有被采样到,而采样到的不好的动作得到了一个比较小的正reward,那么没有被采样到的好动作的出现概率会越来越小,这显然是不合适的,因此我们需要增加一个奖励的基线,让reward有正有负。
一般增加的基线是所获得奖励的平均值:
变为reward-to-go
往往一个动作的reward跟之前的reward没有什么关系。所以这里,将这个序列的reward变为 这个动作及其之后的reward的加和:
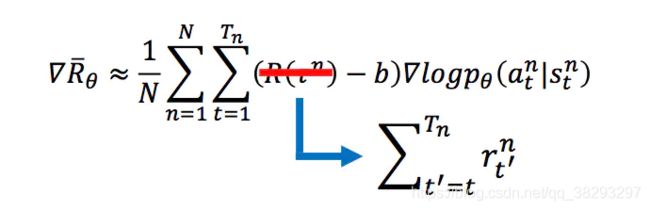
增加折扣因子
这个很容易理解,就像买股票一样,未来的1块钱的价值要小于当前1块钱的价值,因此未来的1块钱变成现在的价值,需要进行一定的折扣
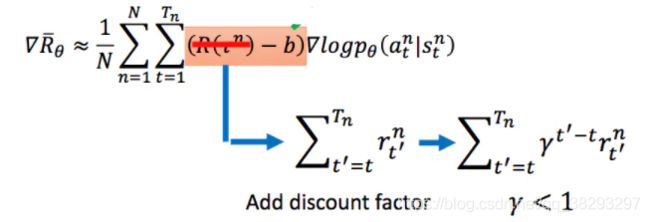
使用优势函数
我们之前介绍的PG方法,对于同一个eposide中的所有数据,使用的奖励都是一样的,其实我们可以将其变为与 s t s_t st 和 a t a_t at 相关的。这里我们使用的是优势函数,即 Q π ( s t , a t ) − V π ( s t ) Q_π(s_t,a_t) - V_π(s_t) Qπ(st,at)−Vπ(st) 。其中 Q π ( s t , a t ) Q_π(s_t,a_t) Qπ(st,at) 可以使用从当前状态开始到eposide结束的奖励折现和得到, V π ( s t ) V_π(s_t) Vπ(st) 可以通过一个critic来计算得到。
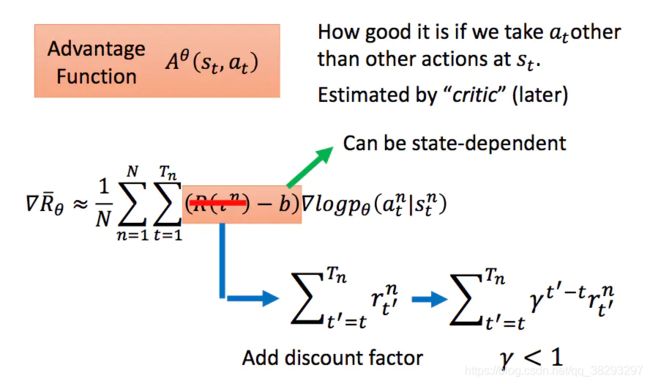
3. PPO算法原理简介
接着上面的讲,PG方法一个很大的缺点就是参数更新慢,因为我们每更新一次参数都需要进行重新的采样,这其实是中on-policy的策略,即我们想要训练的agent和与环境进行交互的agent是同一个agent;与之对应的就是off-policy的策略,即想要训练的agent和与环境进行交互的agent不是同一个agent,简单来说,就是拿别人的经验来训练自己。
那么为了提升我们的训练速度,让采样到的数据可以重复使用,我们可以将on-policy的方式转换为off-policy的方式。即我们的训练数据通过另一个Actor(对应的网络参数为 θ ′ θ' θ′ 得到。这要怎么做呢?通过下面的思路:
- 重要性采样技术将其改为off-policy,重要性采样(IS)的介绍如下
E x ∼ p ( x ) [ f ( x ) ] = ∫ p ( x ) f ( x ) d x = ∫ p ( x ) q ( x ) q ( x ) f ( x ) d x = E x ∼ q ( x ) [ f ( x ) p ( x ) q ( x ) ] ; 红色部分是重要性权重 \begin{aligned} E_{x\sim p(x)}[f(x)]&=\int p(x)f(x)dx\\ &=\int \frac{p(x)}{q(x)}q(x)f(x)dx\\ &=E_{x\sim q(x)}[f(x)\textcolor{red}{\frac{p(x)}{q(x)}}]& \scriptstyle{\text{; 红色部分是重要性权重}}\\ \end{aligned} Ex∼p(x)[f(x)]=∫p(x)f(x)dx=∫q(x)p(x)q(x)f(x)dx=Ex∼q(x)[f(x)q(x)p(x)]; 红色部分是重要性权重
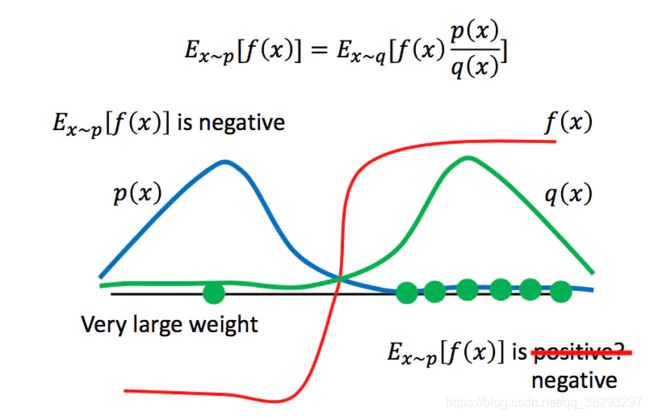
通过重要性采样这种方式,我们的 p ( x ) p(x) p(x) 和 q ( x ) q(x) q(x) 的分布不能差别太大,否则需要进行非常多次的采样,才能得到近似的结果;下面通过一个例子进行说明。
- 如上图所示,很显然,在 x x x 服从 p ( x ) p(x) p(x) 分布时,由图可见,在左半部分 x < 0 x<0 x<0 的时候概率较大,此时 f ( x ) f(x) f(x) 的期望为负;
- 那么此时我们从 q ( x ) q(x) q(x) 中来采样少数的 x x x,那么我们采样到的 x x x 很有可能都分布在右半部分,此时 f ( x ) f(x) f(x) 大于0,我们很容易得到 f ( x ) f(x) f(x) 的期望为正的结论,这就会出现问题,因此需要进行大量的采样。
所以修正后的off-policy style的PG算法的目标函数变为
∇ R ‾ θ = E τ ∼ p θ ′ ( τ ) [ p θ ( τ ) p θ ′ ( τ ) R ( τ ) ∇ l o g p θ ( τ ) ] \nabla \overline R_{\theta} = E_{\tau\sim p_{\theta^{'}}(\tau)}[\frac{p_\theta(\tau)}{p_{\theta^{'}}(\tau)}R(\tau)\nabla log p_\theta(\tau)] ∇Rθ=Eτ∼pθ′(τ)[pθ′(τ)pθ(τ)R(τ)∇logpθ(τ)]
根据上个小节所述的tips,引入baselines方法【减小方差】,同时引入折扣因子(reward-to-go考虑长期收益影响),引入对当前action相对平均值有多好的评价函数,即优势函数 A π ( s t , a t ) A^\pi(s_t,a_t) Aπ(st,at)
推导可以得到新的目标函数如下:

上式中 最后一项因为我们假设两个分布不能差太远,所以认为他们是相等的,为了求解方便,我们直接划掉。此时似然函数变为:
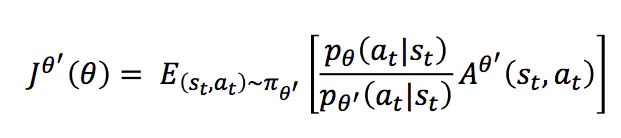
由梯度变为似然函数,使用的是下面式子: ∇ f ( x ) = f ( x ) ∇ l o g f ( x ) \nabla f(x) = f(x) \nabla log f(x) ∇f(x)=f(x)∇logf(x),大家可以自己手动算一下。
我们前面介绍了,我们希望 θ θ θ 和 θ ′ θ' θ′ 不能差太远,这并不是说参数的值不能差太多,而是说,输入同样的state,网络得到的动作的概率分布不能差太远。得到动作的概率分布的相似程度,我们可以用KL散度来计算,将其加入PPO模型的似然函数中,变为:

在实际中,我们会动态改变对 θ θ θ 和 θ ′ θ' θ′ 分布差异的惩罚,如果KL散度值太大,我们增加这一部分惩罚,如果小到一定值,我们就减小这一部分的惩罚,基于此,我们得到了PPO算法的过程:

PPO算法还有另一种实现方式,不将KL散度直接放入似然函数中,而是进行一定程度的裁剪:

上图中,绿色的线代表min中的第一项,即不做任何处理,蓝色的线为第二项,如果两个分布差距太大,则进行一定程度的裁剪。最后对这两项再取min,防止了 θ θ θ 更新太快。
总结一下:
PPO算法加入对off-policy策略引入中的 θ ′ \theta^{'} θ′的约束,设定新的目标函数为
C l i p p e d V e r s i o n J ( θ ) = E t ^ [ min ( r t ( θ ) A t π , c l i p ( r t ( θ , 1 − ϵ , 1 + ϵ ) ) A t π ) ] K L P e n a l t y V e r s i o n J ( θ ) = E t ^ [ r t ( θ ) A t π − β K L [ π θ ′ , π θ ] ] Clipped~Version\quad J(\theta) = \hat{E_t}[\min(r_t(\theta)A^\pi_t, clip(r_t(\theta, 1-\epsilon,1+\epsilon))A^\pi_t)]\\ KL~Penalty~Version\quad J(\theta) = \hat{E_t}[r_t(\theta)A^\pi_t-\beta\mathcal{KL}[\pi_{\theta^{'}},\pi_{\theta}]] Clipped VersionJ(θ)=Et^[min(rt(θ)Atπ,clip(rt(θ,1−ϵ,1+ϵ))Atπ)]KL Penalty VersionJ(θ)=Et^[rt(θ)Atπ−βKL[πθ′,πθ]]
where r t ( θ ) = π θ π θ ′ r_t(\theta)=\frac{\pi_{\theta}}{\pi_{\theta^{'}}} rt(θ)=πθ′πθ,两种方法的目的都是约束两次更新的网络参数分布距离较近,避免不稳定现象
通过以上介绍可以得到PPO算法的基本流程伪代码如下:
for iteration=1,2,... do
for actor=1,2,...N do
Run policy \theta_{old} in env for T timesteps
Compute advantage estimates A
end for
Optimize L for params of actors and critic with batched data
\theta_{old} <-- \theta
end for
4. 特殊说明
几点需要特别说明的
- off-policy体现在只需要用上一次的actor中policy的old参数生成多个trajectory求得loss,再用梯度反向传播方法对新的参数进行更新一次,而不是需要每次都要重新生成数据
- 两个分布相除是在对数域上相减得到
- 算法中提到的 θ ′ \theta^{'} θ′和 θ \theta θ是两次循环更新的值,由于重要性采样得到的公式可以看到期望值是在 θ ′ \theta^{'} θ′上计算的,所以是先用未更新的网络生成trajectory计算loss,经过循环累加用来更新新的 θ \theta θ
算法实现
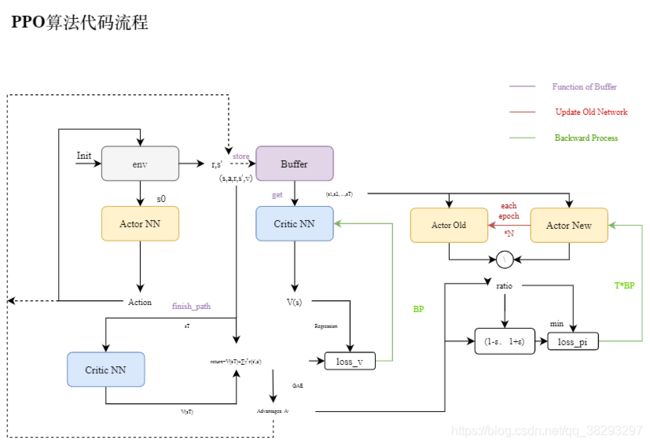
总体流程
代码实现
创建环境
import gym
env = gym.make('Pendulum-v0').unwrapped
得到state、action、reward
这里我们首先得到state,action和即时奖励reward的序列,随后我们要计算折现的奖励和,get_v()是一个得到状态价值的函数。使用v(s) = r + gamma * v(s+1)不断进行循环。
for t in range(EP_LEN): # in one episode
env.render()
a = ppo.choose_action(s) # 根据一个正态分布,选择一个action
s_, r, done, _ = env.step(a)
buffer_s.append(s)
buffer_a.append(a)
buffer_r.append((r+8)/8) # normalize reward, find to be useful
s = s_
ep_r += r
# update ppo
if (t+1) % BATCH == 0 or t == EP_LEN-1:
v_s_ = ppo.get_v(s_)
discounted_r = []
for r in buffer_r[::-1]:
v_s_ = r + GAMMA * v_s_
discounted_r.append(v_s_) # v(s) = r + gamma * v(s+1)
discounted_r.reverse()
bs, ba, br = np.vstack(buffer_s), np.vstack(buffer_a), np.array(discounted_r)[:, np.newaxis]
buffer_s, buffer_a, buffer_r = [], [], []
ppo.update(bs, ba, br)
定义critic计算优势函数
这里我们定义了一个critic来计算优势函数,状态价值定义了一个全联接神经网络来得到,而折扣奖励和我们之前已经计算过了:
#critic
with tf.variable_scope('critic'):
l1 = tf.layers.dense(self.tfs,100,tf.nn.relu)
self.v = tf.layers.dense(l1,1) # state-value
self.tfdc_r = tf.placeholder(tf.float32,[None,1],'discounted_r')
self.advantage = self.tfdc_r - self.v
self.closs = tf.reduce_mean(tf.square(self.advantage))
self.ctrain_op = tf.train.AdamOptimizer(C_LR).minimize(self.closs)
定义Actor
PPO里采用的是off-policy的策略,需要有一个单独的网络来收集数据,并用于策略的更新,同DQN的策略一样,我们定义了一个单独的网络,这个网络的参数是每隔一段时间由我们真正的Actor的参数复制过去的。
#actor
pi,pi_params = self._build_anet('pi',trainable=True)
oldpi,oldpi_params = self._build_anet('oldpi',trainable=False)
with tf.variable_scope('sample_action'):
self.sample_op = tf.squeeze(pi.sample(1),axis=0)
with tf.variable_scope('update_oldpi'):
self.update_oldpi_op = [oldp.assign(p) for p,oldp in zip(pi_params,oldpi_params)]
self.tfa = tf.placeholder(tf.float32,[None,A_DIM],'action')
self.tfadv = tf.placeholder(tf.float32,[None,1],'advantage')
而网络构建的代码如下,这里就比较神奇了,我们的Actor网络输出一个均值和方差,并返回一个由该均值和方差得到的正态分布,动作基于此正态分布进行采样:
def _build_anet(self,name,trainable):
with tf.variable_scope(name):
l1 = tf.layers.dense(self.tfs,100,tf.nn.relu,trainable=trainable)
mu = 2 * tf.layers.dense(l1,A_DIM,tf.nn.tanh,trainable=trainable)
sigma = tf.layers.dense(l1,A_DIM,tf.nn.softplus,trainable=trainable)
norm_dist = tf.distributions.Normal(loc=mu,scale=sigma) # 一个正态分布
params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES,scope=name)
return norm_dist,params
损失计算
采用KL散度或者裁切的方式,损失计算方式不同:
with tf.variable_scope('loss'):
with tf.variable_scope('surrogate'):
ratio = pi.prob(self.tfa)/oldpi.prob(self.tfa)
surr = ratio * self.tfadv
if METHOD['name'] == 'kl_pen':
self.tflam = tf.placeholder(tf.float32,None,'lambda')
kl = tf.distributions.kl_divergence(oldpi,pi)
self.kl_mean = tf.reduce_mean(kl)
self.aloss = -tf.reduce_mean(surr-self.tflam * kl)
else:
self.aloss = -tf.reduce_mean(tf.minimum(surr,tf.clip_by_value(ratio,1.-METHOD['epsilon'],1.+METHOD['epsilon'])*self.tfadv))
本文的代码地址为:https://github.com/princewen/tensorflow_practice/tree/master/RL/Basic-PPO-Demo
参考的是莫烦老师的代码:https://github.com/MorvanZhou/Reinforcement-learning-with-tensorflow/blob/master/contents/12_Proximal_Policy_Optimization/simply_PPO.py
作者:文哥的学习日记
链接:https://www.jianshu.com/p/9f113adc0c50
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。