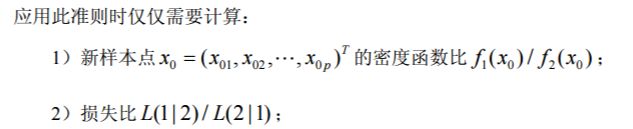判别分析 ( distinguish analysis)(三):Bayes 判别
判别分析系列博文:
判别分析 ( distinguish analysis)(一):距离判别
判别分析 ( distinguish analysis)(二):Fisher 判别
判别分析 ( distinguish analysis)(三):Bayes 判别
判别分析 ( distinguish analysis)(四):应用举例
目录
1.误判概率与误判损失
平均误判损失ECM
2.两总体的 Bayes 判别
Anderson 线性判别函数
例:建立 Anderson 线性判别函数
Bayes 判别和 Bayes 估计的思想方法是一样的,即假定对研究的对象已经有一定的 认识,这种认识常用先验概率来描述,当我们取得一个样本后,就可以用样本来修正已 有的先验概率分布,得出后验概率分布,再通过后验概率分布进行各种统计推断。
1.误判概率与误判损失
设有两个总体 X1和 X2 ,根据某一个判别规则,将实际上为 X1的个体判为 X2 或者将实际上为 X2 的个体判为 X1 的概率就是误判概率,一个好的判别规则应该使误判概率最小。除此之外还有一个误判损失问题或者说误判产生的花费(cost)问题,如把 X1的个体误判到 X2 的损失比 X2 的个体误判到 X1 严重得多,则人们在作前一种判断时就要特别谨慎。譬如在药品检验中把有毒的样品判为无毒后果比无毒样品判为有毒严重得多,因此一个好的判别规则还必须使误判损失最小。
平均误判损失ECM
一个合理的判别规则应使 ECM 达到极小。
2.两总体的 Bayes 判别
Anderson 线性判别函数
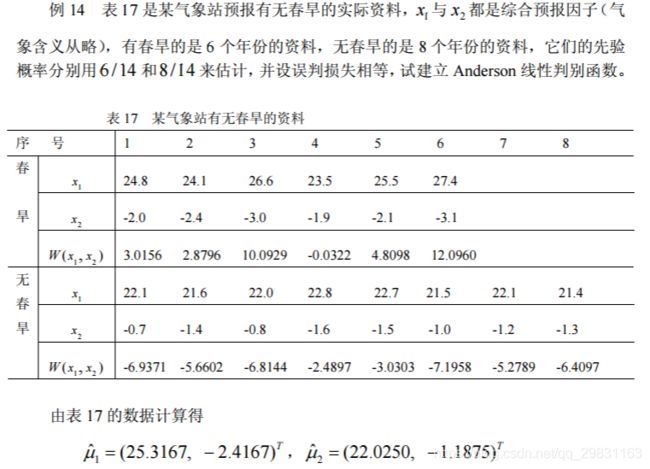
例:建立 Anderson 线性判别函数
计算的 MATLAB 程序如下:
clc,clear
a=[24.8 24.1 26.6 23.5 25.5 27.4
-2.0 -2.4 -3.0 -1.9 -2.1 -3.1]';
b=[22.1 21.6 22.0 22.8 22.7 21.5 22.1 21.4
-0.7 -1.4 -0.8 -1.6 -1.5 -1.0 -1.2 -1.3]';
n1=6;n2=8;
mu1=mean(a);mu2=mean(b);
mu1=mu1',mu2=mu2'
s1=(n1-1)*cov(a),s2=(n2-1)*cov(b)
sigma2=(s1+s2)/(n1+n2-2)
beta=log(8/6)
syms x1 x2
x=[x1;x2];
wx=(x-0.5*(mu1+mu2)).'*inv(sigma2)*(mu1-mu2);
digits(6),wx=vpa(wx)
ahat=subs(wx,{x1,x2},{a(:,1),a(:,2)})
bhat=subs(wx,{x1,x2},{b(:,1),b(:,2)})下面我们编写Σ1 ≠ Σ2 情形下的 MATLAB 程序:
clc,clear
p1=6/14;p2=8/14;
a=[24.8 24.1 26.6 23.5 25.5 27.4
-2.0 -2.4 -3.0 -1.9 -2.1 -3.1]';
b=[22.1 21.6 22.0 22.8 22.7 21.5 22.1 21.4
-0.7 -1.4 -0.8 -1.6 -1.5 -1.0 -1.2 -1.3]';
n1=6;n2=8;
mu1=mean(a);mu2=mean(b);
mu1=mu1',mu2=mu2'
cov1=cov(a),cov2=cov(b)
k=log(p2/p1)+0.5*log(det(cov1)/det(cov2))+0.5*(mu1'*inv(cov1)*mu1-mu2'*inv(
cov2)*mu2)
syms x1 x2
x=[x1;x2];
wx=-0.5*x.'*(inv(cov1)-inv(cov2))*x+(mu1'*inv(cov1)-mu2'*inv(cov2))*x;
digits(6),wx=vpa(wx);
wx=simple(wx)
ahat=subs(wx,{x1,x2},{a(:,1),a(:,2)})
bhat=subs(wx,{x1,x2},{b(:,1),b(:,2)})
ahat>=k,bhat分类正确率为 100%。
判别分析系列博文:
判别分析 ( distinguish analysis)(一):距离判别
判别分析 ( distinguish analysis)(二):Fisher 判别
判别分析 ( distinguish analysis)(三):Bayes 判别
判别分析 ( distinguish analysis)(四):应用举例