Pytorch神经网络基础

学习了李沐——《动手学深度学习》的视频课程，在此对知识点进行整理以及记录动手实践中遇到的一些问题和想法。

一.神经网络的搭建

        首先，我们导入可能用到的包

import torch
from torch import nn
from torch.nn import functional as F

 1.自定义块

        我们可以通过自定义块进行神经网络的初步搭建，这个块中包含一个多层感知机。这个感知机具有256个隐藏单元的隐藏层和一个10维的输出层。在构造搭建神经网络时，每一个class都需要继承torch,nn.Module类，并重写父类的初始化函数__init__()和前向传播函数forward()。        

class MLP(nn.Module):
    # 用模型参数声明层。这里，我们声明两个全连接的层
    def __init__(self):
        # 调用MLP的父类Module的构造函数来执行必要的初始化。
        # 这样，在类实例化时也可以指定其他函数参数，例如模型参数params（稍后将介绍）
        super().__init__()
        self.hidden = nn.Linear(20, 256)  # 隐藏层
        self.out = nn.Linear(256, 10)  # 输出层

    # 定义模型的前向传播，即如何根据输入X返回所需的模型输出
    def forward(self, X):
        # 注意，这里我们使用ReLU的函数版本，其在nn.functional模块中定义。
        return self.out(F.relu(self.hidden(X)))

        我们在初始化函数中，定义神经网络的每一层，可以看到，我们在此声明了两个全连接层。在前向传播函数中，它以x作为输入，经过hidden层，再使用激活函数进行输出，之后再次进入out层，作为最后的输出。

        上述代码是《动手学深度学习》书中的示例代码。笔者自己的代码如下：

class Mlp(nn.Module):
    
    def __init__(self):
        super().__init__()
        self.hidden = nn.Linear(20, 256)
        self.out = nn.Linear(256, 10)
        
    def forward(self, X):
        X = self.hidden(X)
        X = F.relu(X)
        X = self.out(X)
        
        return X

        这段代码与书中区别不大，只不过是将relu函数写在了__init__()中。

        接下来，我们使用以下这个方法。

net = Mlp()

X = torch.rand(2, 20)
y_hat = net(X)

        我们随机生成了一个2x20的矩阵X作为输入，y_hat为输出，我们得到的结果如下。

tensor([[ 0.1855, -0.0653, -0.0294,  0.0289, -0.3788, -0.3535,  0.0319,  0.2367,
          0.0234,  0.1758],
        [ 0.1773, -0.1185,  0.1917,  0.1266, -0.3549, -0.3114,  0.0384,  0.2747,
         -0.0602,  0.2141]], grad_fn=)

         块的一个主要优点是它的多功能性。 我们可以子类化块以创建层（如全连接层的类）、 整个模型（如上面的MLP类）或具有中等复杂度的各种组件。 我们在接下来的章节中充分利用了这种多功能性， 比如在处理卷积神经网络时。

2.顺序块

        书中对于顺序块的讲述，使用到了自定义简化的块MySequential，可能工作原理与nn.Sequential类是一样的。

class MySequential(nn.Module):
    def __init__(self, *args):
        super().__init__()
        for idx, module in enumerate(args):
            # 这里，module是Module子类的一个实例。我们把它保存在'Module'类的成员
            # 变量_modules中。_module的类型是OrderedDict
            self._modules[str(idx)] = module

    def forward(self, X):
        # OrderedDict保证了按照成员添加的顺序遍历它们
        for block in self._modules.values():
            X = block(X)
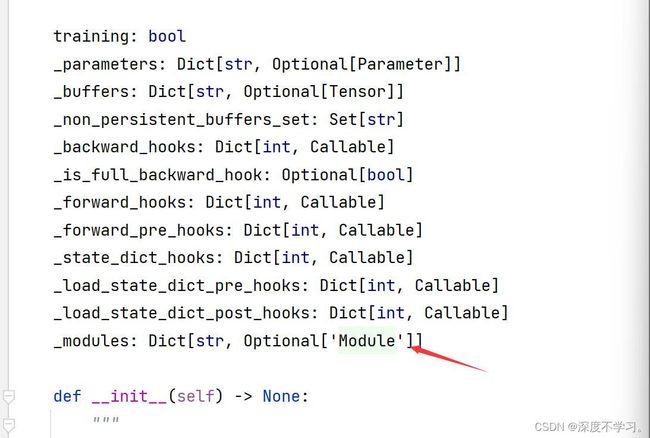
        return X

        在笔者自己重写这个类的时候，误将self._modules写成了self.modules_，后来程序报错，经过查询后才知道，_modules是nn.Module中固有的一个属性，通过Pycharm打开nn.Moudle中可以看到这个属性的声明。

         在_modules这个属性中，保存了这个神经网络每一层的定义，我们可以将这个属性print一下看看。

net = MySequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10))
print("#############################")
print(net._modules)
print("#############################")
print(net(X))

        我们往自定义的顺序块中定义了一个多层感知机，输出的结果如下。

#############################
OrderedDict([('0', Linear(in_features=20, out_features=256, bias=True)), ('1', ReLU()), ('2', Linear(in_features=256, out_features=10, bias=True))])
#############################
tensor([[ 0.0451,  0.0506,  0.0708,  0.1691, -0.0690,  0.2757,  0.1234,  0.0643,
          0.2320,  0.1050],
        [ 0.0815, -0.0634,  0.1051,  0.1634, -0.0173,  0.3460,  0.0656,  0.1276,
          0.2268,  0.1578]], grad_fn=)

        可以看到，_modules属性中，存储了我们声明的每一层。

二.在前向传播函数中执行代码

        前向传播函数就是class类中写到的forward()函数。当我们需要更强的灵活性，或者需要在神经网络中进行某种自定义的数学运算，就可以用到这个函数。

        例如，在上述例子中的多层感知机，我们想额外增加两个操作：

• 自己编写Relu函数，即  XW + b。
• 使得最后输出的L1范数小于1

class FixedHiddenMLP(nn.Module):
    def __init__(self):
        super().__init__()
        # 不计算梯度的随机权重参数。因此其在训练期间保持不变
        self.rand_weight = torch.rand((20, 20), requires_grad=False)
        self.linear = nn.Linear(20, 20)
        
    def forward(self, X):
        X = self.linear(X)
        
        X = F.relu(X @ self.rand_weight + 10)
        # 为了保证后面L1范数的约束效果，我们把bias设置大一些
        X = self.linear(X)
        
        while X.abs().sum() > 1:
            X /= 2
            
        return X.sum()

X = torch.rand(2, 20)
net = FixedHiddenMLP()
y_hat = net(X)
print(y_hat)

        我们来看一下最后的输出。

tensor(0.1166, grad_fn=)

三.神经网络中的参数获取与初始化

        我们首先看一下单隐藏层的多层感知机

import torch
from torch import nn

net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(), nn.Linear(8, 1))
X = torch.rand(size=(2, 4))
net(X)

tensor([[-0.4626],
        [-0.5465]], grad_fn=)

1.参数访问

        当我们用Sequential()类定义模型的时候，我们可以通过索引来访为模型的任意层。这就像模型是一个列表一样，每层的参数都在其属性中。 如下所示，我们可以检查第二个全连接层的参数。

print(net[2].state_dict())

OrderedDict([('weight', tensor([[-0.1514, -0.2675, -0.3112, -0.1464,  0.0989,  0.3014,  0.1620, -0.1384]])), ('bias', tensor([-0.3249]))])

        这个输出表示，在第三层，也就是神经网络的第二个全连接层中，包含两个参数，第一个是权重weight 和偏置bias，二者都已单精度浮点数float32的方式储存。

        可以看到，上一行代码中，我们使用到了state_dict()的方法，我们来看一下这个方法的官方解释。

    def state_dict(self, *args, destination=None, prefix='', keep_vars=False):
        r"""Returns a dictionary containing references to the whole state of the module.

        Both parameters and persistent buffers (e.g. running averages) are
        included. Keys are corresponding parameter and buffer names.
        Parameters and buffers set to ``None`` are not included.

        方法定义中表示，该方法可以返回包含对模块整个状态的引用的字典。既然是个字典，我们就可以通过字典索引的方法获取值。当我们执行了net[2].state_dict()这一行代码时，可以看到整个字典中，有两个键，分别是weight和bias，下面，我们就可以直接通过键值对索引的方法获取参数了。注意不要忘记引号。

print(net[2].state_dict()['weight'])
print(net[2].state_dict()['bias'])

tensor([[-0.0272, -0.0133, -0.3240,  0.3132, -0.1283,  0.2246,  0.1192, -0.2657]])
tensor([-0.0799])

        起初照着教材敲代码的时候，笔者有个疑惑，这个data属性是怎么来的，看到返回的属性是一个tensor数据类型，于是打开了torch.tensor()的文档，发现data是该方法的属性。

def tensor(data: Any, dtype: Optional[_dtype]=None, device: Device=None, requires_grad: _bool=False) -> Tensor: ...

         上文中，我们只获取了神经网络其中一层的参数，接下来我们可以尝试着获取神经网络中每一层的参数，我们直接暴力一点。

print(net.state_dict())

OrderedDict(
[('0.weight', tensor([[-0.3578, -0.0779, -0.4654,  0.2061],
        [-0.2745,  0.2116,  0.0571,  0.0851],
        [-0.0334,  0.3411, -0.3570,  0.0618],
        [ 0.1501,  0.1214, -0.0715,  0.1124],
        [ 0.2564, -0.4512,  0.3402, -0.4430],
        [ 0.3695,  0.2382, -0.2993, -0.1740],
        [-0.1359, -0.0580, -0.0948, -0.4430],
        [ 0.0654, -0.2478, -0.4690, -0.1755]])), 
('0.bias', tensor([ 0.1552, -0.3691, -0.3870,  0.3516,  0.2946, -0.1366, -0.4313,  0.2209])), 
('2.weight', tensor([[-0.0272, -0.0133, -0.3240,  0.3132, -0.1283,  0.2246,  0.1192, -0.2657]])), 
('2.bias', tensor([-0.0799]))])

        这里可以看到，整个字典中一共有4对键值对，由此可以分析出，键的命名方式就是“层数.参数名称”。也就说，我们获取到了第1层和第3层的两个参数，而没有获取第二层的参数，因为在这个网络中，第二层是一个ReLU()，该方法并没有参数的设置，只是起到激活作用。因此，我们就获得了另一种访问网络参数的方式。

print(net.state_dict()['0.weight'].data)
print(net.state_dict()['0.bias'].data)
print(net.state_dict()['2.weight'].data)
print(net.state_dict()['2.bias'].data)

tensor([[-0.3578, -0.0779, -0.4654,  0.2061],
        [-0.2745,  0.2116,  0.0571,  0.0851],
        [-0.0334,  0.3411, -0.3570,  0.0618],
        [ 0.1501,  0.1214, -0.0715,  0.1124],
        [ 0.2564, -0.4512,  0.3402, -0.4430],
        [ 0.3695,  0.2382, -0.2993, -0.1740],
        [-0.1359, -0.0580, -0.0948, -0.4430],
        [ 0.0654, -0.2478, -0.4690, -0.1755]])
tensor([ 0.1552, -0.3691, -0.3870,  0.3516,  0.2946, -0.1366, -0.4313,  0.2209])
tensor([[-0.0272, -0.0133, -0.3240,  0.3132, -0.1283,  0.2246,  0.1192, -0.2657]])
tensor([-0.0799])

        上文中，我们提到，当我们使用nn.Sequential()方法创建一个神经网络的时候，我们可以直接使用层数的下标索引值获取参数。方法如下。

print(net[0].weight.data)
print(net[0].bias.data)
print(net[2].weight.data)
print(net[2].bias.data)

2.从嵌套块中访问参数

        让我们看看，如果我们将多个块相互嵌套，参数命名约定是如何工作的。 我们首先定义一个生成块的函数（可以说是“块工厂”），然后将这些块组合到更大的块中。

def block1():
    return nn.Sequential(nn.Linear(4, 8), nn.ReLU(),
                         nn.Linear(8, 4), nn.ReLU())

def block2():
    net = nn.Sequential()
    for i in range(4):
        # 在这里嵌套
        net.add_module(f'block {i}', block1())
    return net

rgnet = nn.Sequential(block2(), nn.Linear(4, 1))
y_hat = rgnet(X)
print(y_hat)
print(rgnet)

tensor([[-0.3078],
        [-0.3078]], grad_fn=)

Sequential(
  (0): Sequential(
    (block 0): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
    (block 1): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
    (block 2): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
    (block 3): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
  )
  (1): Linear(in_features=4, out_features=1, bias=True)
)

        因为层是分层嵌套的，所以我们也可以像通过嵌套列表索引一样访问它们。 下面，我们访问第一个主要的块中、第二个子块的第一层的偏置项，以及最后一个全连接层的偏置项。

print(rgnet[0][1][0].bias.data)
print(rgnet[1].bias.data)

tensor([-0.4040,  0.1900, -0.0780,  0.1957, -0.2150,  0.0059, -0.4671, -0.2036])
tensor([0.4097])

3.参数初始化

        在神经网络中，参数初始化是十分有必要的。参数初始化也是建立一个神经网络的必要工作。

（1）.内置初始化

        Pytorch在torch.nn模块中，已经写好了若干内置的初始化器，我们可以直接调用这些初始化器实现参数的初始化。具体的初始化器读者可以通过查看官方的定义。

        下面的代码，我们将所有权重参数初始化为标准差为0.01的正态随机变量，将所有的偏置参数设置成0。

        

def init_normal(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, mean=0, std=0.01)
        nn.init.zeros_(m.bias)
net.apply(init_normal)
print(net[0].weight.data[0])
print(net[0].bias.data[0])

(tensor([-0.0128, -0.0141,  0.0062,  0.0028])
(tensor(0.))

        我们还可以将所有参数属初始化为常数。

def init_constant(m):
    if type(m) == nn.Linear:
        nn.init.constant_(m.weight, 1)
        nn.init.zeros_(m.bias)
net.apply(init_constant)
print(net[0].weight.data[0])
print(net[0].bias.data[0])

(tensor([1., 1., 1., 1.])
(tensor(0.))

        我们还可以对某些不同的层设置不同的初始化方法。例如，下面我们使用Xavier初始化方法初始化第一个神经网络层， 然后将第三个神经网络层初始化为常量值42。

def init_xavier(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform_(m.weight)
def init_42(m):
    if type(m) == nn.Linear: 
        nn.init.constant_(m.weight, 42)

net[0].apply(init_xavier)
net[2].apply(init_42)
print(net[0].weight.data[0])
print(net[2].weight.data)

tensor([ 0.3809,  0.5354, -0.4686, -0.2376])
tensor([[42., 42., 42., 42., 42., 42., 42., 42.]])

（2）.自定义初始化

        有时候，Pytorch框架并没有给出我们想要的初始化，我们也可以根据自己的需求进行设置。比如，我们使用以下的分布来初始化权重参数。

def my_init(m):
    if type(m) == nn.Linear:
        print("Init", *[(name, param.shape)
                        for name, param in m.named_parameters()][0])
        nn.init.uniform_(m.weight, -10, 10)
        m.weight.data *= m.weight.data.abs() >= 5

net.apply(my_init)
print(net[0].weight[:2])

Init weight torch.Size([8, 4])
Init weight torch.Size([1, 8])
tensor([[-0.0000, 0.0000, -0.0000, 0.0000],
        [-0.0000, 9.3464, 5.5061, 6.8197]], grad_fn=)

 (3）.参数绑定

        书中在本章的最后还提到了一个参数绑定的概念，其目的是在多层之间共享参数。

        我们定义一个全连接层，然后使用它的参数来设置另一个层的参数。

# 我们需要给共享层一个名称，以便可以引用它的参数
shared = nn.Linear(8, 8)
net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(),
                    shared, nn.ReLU(),
                    shared, nn.ReLU(),
                    nn.Linear(8, 1))
net(X)
# 检查参数是否相同
print(net[2].weight.data[0] == net[4].weight.data[0])
net[2].weight.data[0, 0] = 100
# 确保它们实际上是同一个对象，而不只是有相同的值
print(net[2].weight.data[0] == net[4].weight.data[0])

tensor([True, True, True, True, True, True, True, True])
tensor([True, True, True, True, True, True, True, True])

四.突发奇想

        学习完之后，笔者突发奇想，想尝试一下利用一个神经网络实现矩阵的运算操作，具体想法如下。

       

          实现代码如下：

def init_paras_shared(m):
    torch.nn.init.constant_(m.weight, 2)
    torch.nn.init.zeros_(m.bias)

def init_paras_Linear(m):
    torch.nn.init.constant_(m.weight, 4)
    torch.nn.init.constant_(m.bias, 1)

shared = nn.Linear(5, 5)

net = nn.Sequential(
    shared, 
    shared, 
    nn.Linear(5, 1)
)


shared.apply(init_paras_shared)
net[2].apply(init_paras_Linear)

X = torch.arange(1, 6, dtype=torch.float32)
y_hat = net(X)
print(y_hat)

tensor([6001.], grad_fn=)

        头次写稿，若有不足，还请各路大牛批评指出。