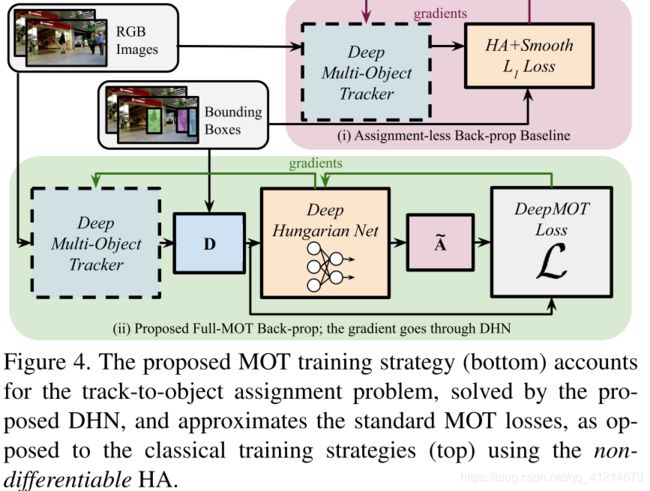
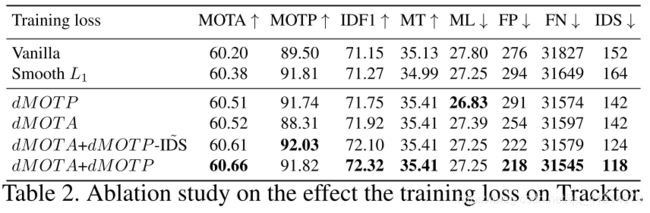
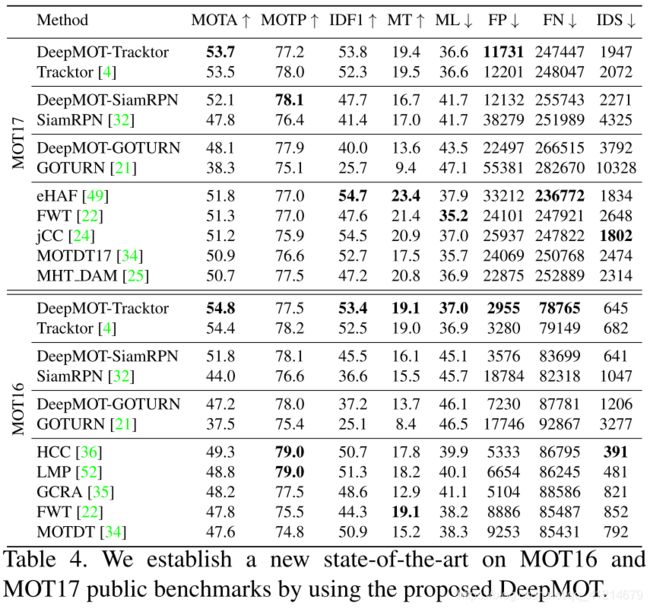
一个可微的轨迹训练方法:How To Train Your Deep Multi-Object Tracker
论文地址:链接
代码地址:链接
How To Train Your Deep Multi-Object Tracker
- 一、 介绍
- 二、 DeepMOT
-
- 深度匈牙利算法:DHN
- MOTA和MOTP微分操作
- 如何训练深度多目标追踪器
- 三、 实验
主要贡献:
- 提出了新颖的损失函数直接激发MOT评价指标,进行端到端训练MOT追踪器。
- 为了使得反向传播损失通过网络,提出了新的模型DHN来以可微的方式来进行匹配预测轨迹和GT目标。
- 通过实现证明了提出的损失函数和可微匹配的有效性,MOTChallenge上达到了SOTA。
一、 介绍
在大多数独立训练的方法中,通常会使用多个损失分别优化不同的任务。然而有一个匹配任务,通常难以定义损失,因为他需要计算预测的目标轨迹和GT目标之间的优化匹配,大多数方法使用匈牙利算法(HA)来代替,然而HA又是不可微分的操作。
作者提出了一个新颖的训练MOT追踪器的框架DeepMOT以及包括直接关联已建立的评估标准的损失函数。主要成分DHN提供了一个优化预测和GT分配的软近似,允许梯度的反传,从而更新追踪器。
提出的近似是基于一个双向递归神经网络,基于预测和GT目标之间的距离矩阵计算分配矩阵。然后将MOTA和MOTP表示为计算得到的(软)分配矩阵和距离矩阵的可微函数。
通过DHN,将近似追踪指标的梯度传播回去来更新追踪器。如此,可以使用直接关联指标的损失来训练追踪器。
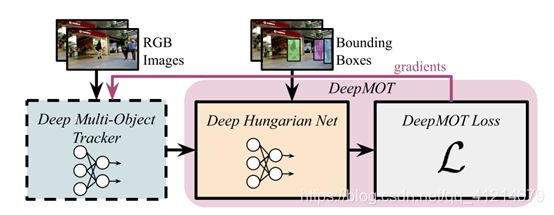
目前也有在追踪阶段使用损失的,但不是直接关联追踪指标的,基本都是局部训练的,也不知如何训练来达到最大评估指。例如有些就是学习一个表达目标的embedding,用于数据关联,常用到对比、三元组等损失函数。推理的时候就直接使用这些embedding来计算相似度。现在的网络,匹配大部分还是使用的匈牙利算法,有些方法提出了匹配的损失,但仅仅是学习最后的数据关联函数,本方法可以运用到任何可学习的追踪方法。
二、 DeepMOT
由于只要得到了预测轨迹和真实轨迹,就可以相应的计算出TP,FN,IDS。本方法沿着二阶段的策略,受MOTA和MOTP计算的启发,提出了一个可微的损失。一旦匹配建立,设计一个损失,近似评估标准,作为软分配矩阵和距离矩阵的可微函数的组合。
深度匈牙利算法:DHN
DHN产生了一个关于距离矩阵 D \bm D D的可微代理 A ~ \widetilde \bm A A ,因此会在损失和追踪器之间产生一个桥梁来传送梯度。使用一个非线性的映射来表示DHN,输入为 D \bm D D,输出为代理软分配矩阵 A ~ \widetilde \bm A A 。
建模为: A ~ = g ( D , ω d ) \tilde{\mathbf{A}}=g\left(\mathbf{D}, \omega_{d}\right) A~=g(D,ωd),参数为 ω d \omega_{d} ωd。其映射必须满足以下几个规则:
- 输出的 A ~ \widetilde \bm A A 必须很好近似分配矩阵 A ∗ \bm A^* A∗
- 这个近似必须关于 D \bm D D可微
- 输入和输出矩阵等价,但大小不同
- g g g必须像HA一样做出全局决策
DHN结构如下:

行级和列级展平是受匈牙利算法按行和列顺序执行缩减和验证启发,Bi-RNN允许全局进行处理,对所有输入进行解释。如果使用全卷积来替代Bi-RNN,虽然可以处理不同尺寸的输入输出,但是局部的感受野会导致局部分配的决定问题。
这里首先进行行级展开,然后送入Bi-RNN输出第一步的隐藏表达,大小为 N × M × 2 h N\times M\times 2h N×M×2h, h h h表示Bi-RNN的隐藏层尺寸,第一阶段的隐藏表示对行式的中间分配进行编码。然后将该表示列级展开,送入第二个Bi-RNN,获得第二个隐藏表示,大小为 N × M × 2 h N\times M\times 2h N×M×2h。两个Bi-RNN隐藏层相同,不共享权重。第二个隐藏表示就是最后分配的编码,将他送入三个全连接层进行解码获得软分配矩阵 A ~ \widetilde \bm A A ,大小 N × M N\times M N×M。
对比HA的二值输出,DHN输出一个软分配矩阵 A ~ ∈ [ 0 , 1 ] N × M \widetilde \bm A \in [0,1]^{N\times M} A ∈[0,1]N×M。
距离矩阵 D \bm D D的计算
大多数常见计算为两个Bbox 的IoU,原则上式可以被微分的,但是当两个Bbox没有交集的时候,距离1-IoU将会为常量1,如此梯度则为0,则传播了个寂寞。
所以这里作者选择了使用中心点的欧氏距离和Jaccard距离 J \mathcal J J(定义为1-IoU)的均值来作为距离:
d n m = f ( x n , y m ) + J ( x n , y m ) 2 (1) d_{n m}=\frac{f\left(\mathbf{x}^{n}, \mathbf{y}^{m}\right)+\mathcal{J}\left(\mathbf{x}^{n}, \mathbf{y}^{m}\right)}{2} \tag{1} dnm=2f(xn,ym)+J(xn,ym)(1)
f f f是关于图片大小的欧氏距离:
f ( x n , y m ) = ∥ c ( x n ) − c ( y m ) ∥ 2 H 2 + W 2 (2) f\left(\mathbf{x}^{n}, \mathbf{y}^{m}\right)=\frac{\left\|c\left(\mathbf{x}^{n}\right)-c\left(\mathbf{y}^{m}\right)\right\|_{2}}{\sqrt{H^{2}+W^{2}}} \tag{2} f(xn,ym)=H2+W2∥c(xn)−c(ym)∥2(2)
c ( ⋅ ) c(·) c(⋅)计算边界框中心点, H , W H,W H,W为视频帧的宽高。
由于距离经过标准化处理都在0-1范围内,所有的 d n m ∈ [ 0 , 1 ] d_{nm}\in [0,1] dnm∈[0,1],这样任何的距离都是可微的。
MOTA和MOTP微分操作
这里详细介绍MOTA的微分dMOTA和MOTP的微分dMOTP的计算过程。 MOTA = 1 − ∑ t ( F P t + F N t + I D S t ) ∑ t M t \text { MOTA }=1-\frac{\sum_{t}\left(\mathrm{FP}_{t}+\mathrm{FN}_{t}+\mathrm{IDS}_{t}\right)}{\sum_{t} M_{t}} MOTA =1−∑tMt∑t(FPt+FNt+IDSt) M O T P = ∑ t ∑ n , m d t n m a t n m ∗ ∑ t ∣ T P t ∣ \mathrm{MOTP}=\frac{\sum_{t} \sum_{n, m} d_{t n m} a_{t n m}^{*}}{\sum_{t}\left|\mathrm{TP}_{t}\right|} MOTP=∑t∣TPt∣∑t∑n,mdtnmatnm∗
基于分配矩阵 A ∗ \bm A^* A∗,可以计算出FN,FP,IDS。为了计算dMOTA和dMOTP,需要将这些参数使用DHN表示为 D \bm D D和 A ~ \widetilde \bm A A d的微分函数。
操作如下:
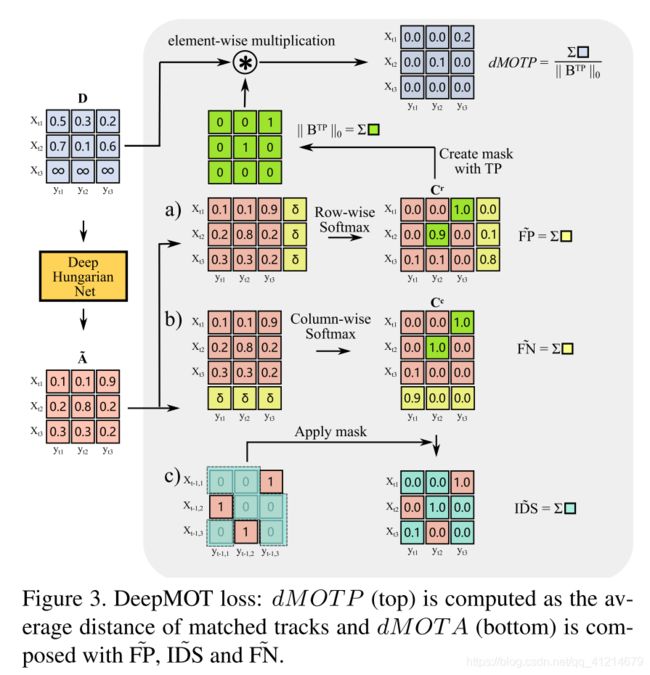
首先需要计算DN和FP,然后需要获得未匹配轨迹和未匹配的GT目标的计数。为此,首先构建一个通过为 A ~ \widetilde \bm A A 增加一列,使用一个阈值δ(例如δ=0.5)填满,获得矩阵 C r C^r Cr,执行行级softmax(图3a)。同样通过对 A ~ \widetilde \bm A A 增加一个行,执行列级softmax(图3b)。然后就可以表达一个FP和FN的软近似数目:
F P ~ = ∑ n C n , M + 1 r , F N ~ = ∑ m C N + 1 , m c (3) \tilde{\mathrm{FP}}=\sum_{n} \mathbf{C}_{n, M+1}^{r}, \quad \tilde{\mathrm{FN}}=\sum_{m} \mathbf{C}_{N+1, m}^{c} \tag{3} FP~=n∑Cn,M+1r,FN~=m∑CN+1,mc(3)
直观看,如果 A ~ \widetilde \bm A A 中所有元素都小于阈值,则最后 C n , M + 1 r , C N + 1 , m c \mathbf{C}_{n, M+1}^{r},\mathbf{C}_{N+1, m}^{c} Cn,M+1r,CN+1,mc就会接近1。标志着存在一个FP或者FN。否则 C r , C c C^r,C^c Cr,Cc中的每行没列的最大元素就会趋近于1,意味着获得了匹配。最终求和获得一个近似于FP和FN的估计 F P ~ , F N ~ \tilde{\mathrm{FP}},\tilde{\mathrm{FN}} FP~,FN~。
为了计算 I D S ~ \tilde{\mathrm{IDS}} IDS~和dMOTP,需要额外建立两个二分矩阵 B T P , B − 1 T P \bm B^{TP},\bm B^{TP}_{-1} BTP,B−1TP,非零条目分别表示在当前帧和前一帧为真正TP。这些矩阵的行索引对应于分配给我们的轨迹的索引,而列索引对应于GT对象。还需要对 B − 1 T P \bm B^{TP}_{-1} B−1TP进行元素级乘法,因为帧之间的目标和轨迹数目不同。通过填充 B − 1 T P \bm B^{TP}_{-1} B−1TP的行和列,来发现当前帧新的目标。注意不需要修改 B T P \bm B^{TP}_{} BTP来弥补新出现的目标,因为这不会造成IDS。如此 C 1 : N , 1 : M c ⊙ B ‾ − 1 T P \mathbf{C}_{1: N, 1: M}^{c} \odot \overline{\mathbf{B}}_{-1}^{\mathrm{TP}} C1:N,1:Mc⊙B−1TP( B ‾ \overline{\mathbf{B}} B是 B \mathbf{B} B的二进制补码)求和后就是IDS的数目: I D S = ∥ C 1 : N , 1 : M c ⊙ B ‾ − 1 T P ∥ 1 (4) \mathrm{ID} \mathrm{S}=\left\|\mathbf{C}_{1: N, 1: M}^{c} \odot \overline{\mathbf{B}}_{-1}^{\mathrm{TP}}\right\|_{1}\tag{4} IDS=∥∥∥C1:N,1:Mc⊙B−1TP∥∥∥1(4)
∥ ⋅ ∥ \|· \| ∥⋅∥是一个展平矩阵的L1范数,有了这些梯度,就可以计算dMOTA:
d M O T A = 1 − F P ~ + F N ~ + γ I D S ~ M (5) d M O T A=1-\frac{\tilde{\mathrm{FP}}+\tilde{\mathrm{FN}}+\gamma \tilde \mathrm{IDS}}{M}\tag{5} dMOTA=1−MFP~+FN~+γIDS~(5)
γ γ γ是对 I D S ~ \tilde \mathrm{IDS} IDS~的惩罚,相似的定义dMOTP:
d M O T P = 1 − ∥ D ⊙ B T P ∥ 1 ∥ B T P ∥ 0 (6) d M O T P=1-\frac{\left\|\mathbf{D} \odot \mathbf{B}^{\mathrm{TP}}\right\|_{1}}{\left\|\mathbf{B}^{\mathrm{TP}}\right\|_{0}} \tag{6} dMOTP=1−∥BTP∥0∥∥D⊙BTP∥∥1(6)
用L1范式表示距离,0范式 ∥ ⋅ ∥ \|·\| ∥⋅∥表示匹配的数量。
提出了相应的损失来最大化MOTA和MOTP: L DeepMOT = ( 1 − d M O T A ) + λ ( 1 − d M O T P ) (7) \mathcal{L}_{\text {DeepMOT }}=(1-d M O T A)+\lambda(1-d M O T P)\tag{7} LDeepMOT =(1−dMOTA)+λ(1−dMOTP)(7) λ λ λ是平衡因子。通过最小化损失,来惩罚FP、FN和IDS,dMOTA和dMOTP必须逐帧计算。
如何训练深度多目标追踪器
总体过程如下,随机采样一对连续帧,两个图片和他们的GT框一起构成一个训练实例。
对于每个实例,首先由t帧的GT框初始化轨迹,运行前向传递以获得t+1帧视频中轨道的边界框预测,为了模拟不完美检测的效果,在GT边界框中添加随机扰动。之后可以计算D以及使用DHN计算 A ~ \widetilde \bm A A ,基于这两个来计算代理损失,从而提供梯度来解释分配,从而更新检测器。
三、 实验
DHA训练细节
为了训练DHA,构建了一个成对矩阵( D D D和 A ∗ A^* A∗),分离为训练集和测试集。 D D D使用GT框和MOTChallenge提供的Public检测计算距离矩阵 D D D,使用HA产生相应的分配矩阵 A ∗ A^* A∗。使用 w 0 , w 1 w_0,w_1 w0,w1来平衡 A ∗ A^* A∗中的类不平衡, w 0 = n 1 / ( n 0 + n 1 ) w_{0}=n_{1} /\left(n_{0}+n_{1}\right) w0=n1/(n0+n1), w 1 = 1 − w 0 w_{1}=1-w_{0} w1=1−w0。使用WA来评价DHA的表现: W A = w 1 n 1 ∗ + w 0 n 0 ∗ w 1 n 1 + w 0 n 0 (8) \mathrm{WA}=\frac{w_{1} n_{1}^{*}+w_{0} n_{0}^{*}}{w_{1} n_{1}+w_{0} n_{0}}\tag{8} WA=w1n1+w0n0w1n1∗+w0n0∗(8)
n 1 ∗ , n 0 ∗ n_1^*,n_0^* n1∗,n0∗分别为TP和FP个数。