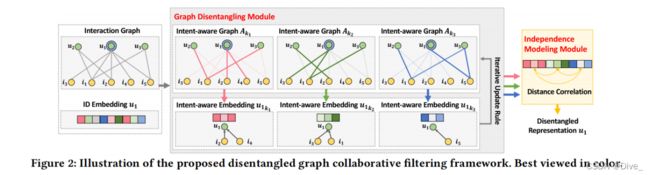
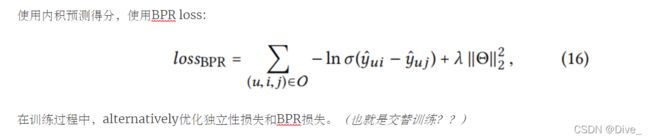2020-SIGIR-Disentangled Graph Collaborative Filtering
DGCF
Abstract
CF演化，从单一的用户-物品交互演化到使用整个交互图来学习表示。这些方法都是uniform方法，忽略了用户采取物品时意图的多样性。本文提出DGCF，分离意图因素，产生解耦表示。
1 INTRODUCTION
DGCF，在用户意图上解耦用户和物品的表示。
- 首先将每一个用户/物品的嵌入划分成块，将每个块和每种隐含的意图耦合。
- 然后采用图解耦模块，带有邻居路由和嵌入传播
- 同时，独立建模模块，使得不同意图尽量独立
2 PRELIMINARY AND RELATED WORK
2.2 任务定义
2.2.1 探索用户—物品关系
学习分布 A ( u , i ) = ( A 1 ( u , i ) , . . . , A K ( u , i ) ) A(u,i)=(A_1(u,i),...,A_K(u,i)) A(u,i)=(A1(u,i),...,AK(u,i))
A K ( u , i ) A_K(u,i) AK(u,i) 表示用户u采取物品i，在第K个意图上的置信度。
2.2.2 生成解耦表示
每个用户的表示为：
e u = ( e 1 u , e 2 u , . . . , e K u ) e_u=(e_{1u},e_{2u},...,e_{Ku}) eu=(e1u,e2u,...,eKu)
e k u e_{ku} eku是用户u在第k个意图的表示
3 METHODOLOGY
3.1 图解耦模块
3.1.1 意图感知的嵌入 初始化
3.1.2 意图感知图 初始化
先前工作不足，只采用一个用户-物品交互图或者一个同质的评分图来表现用户和物品的关系。
定义了K个分数矩阵， S ( u , i ) = [ S 1 ( u , i ) , S 2 ( u , i ) , . . . , S K ( u , i ) ] S(u,i)=[ S_1(u,i),S_2(u,i),...,S_K(u,i) ] S(u,i)=[S1(u,i),S2(u,i),...,SK(u,i)]，初始化都为1。 S k ( u , i ) S_k(u,i) Sk(u,i) 定义用户u和物品i在意图k上之间的交互。初始化都为1，假设建模开始时意图的相同贡献相同。
相当于把之前单个的邻接矩阵A，分成了K个意图分数矩阵S。
3.1.3 图解耦层
3.1.4 层组合
3.2 独立建模模块
3.3 模型优化
3.4 模型分析
- mdel size：和MF参数量相同，也就是K个嵌入表，但是K个嵌入total和MF相同。
- LightGCN：LightGCN相当于只有1种意图、并且没有独立建模的DGCF；这两种模型在准确率上相似，但DGCF能提供可解释性。
- 胶囊网络：可以将分块表示看作胶囊，将迭代更新规则看作动态路由；胶囊网络能够在不同层之间传递信息，DGCF还能在相同层之间传递信息（邻居）。
- 多头注意力网络：意识感知图可以看作多头注意力机制中的channels，但是作用不同。
- DisenGCN：也是用于图表示的解耦，使用GCN。
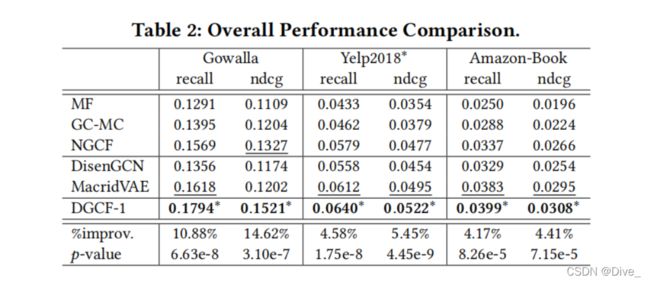
4 EXPERIMENTS
三个问题，常见格式
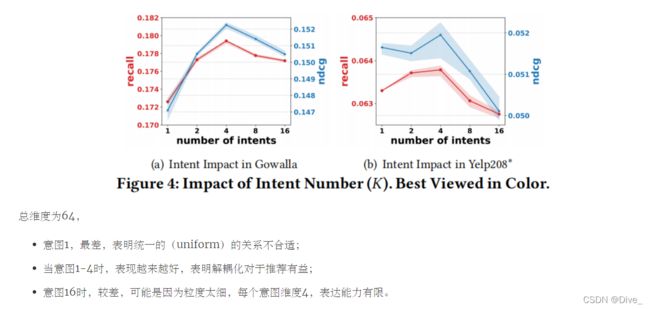
4.1 实验设置
参数设置：64、Adam、Xarvier、迭代2次、网格搜索{学习率、L2正则化系数}
4.2 模型表现
4.3 消融实验
图解耦层数
意图数量
独立建模
4.4 意图解耦、可解释性
意图的解耦化
表示的可解释性
