一、堆的基础
1.1 优先队列和堆
优先队列(Priority Queue):特殊的“队列”,取出元素顺序是按元素优先权(关键字)大小,而非元素进入队列的先后顺序。
若采用数组或链表直接实现优先队列,代价高。依靠数组,基于完全二叉树结构实现优先队列,即堆效率更高。一般来说堆代指二叉堆。
优先队列的完全二叉树(堆)表示
1.2 堆
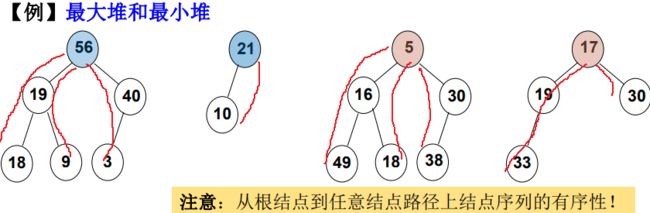
堆序性: 父节点元素值比孩子节点大(小)
- 最大堆(MaxHeap), 也称“大顶堆”:根节点为最大值;
- 最小堆(MinHeap), 也称“小顶堆” :根节点为最小值。
通常以最大堆为例。 最小堆实现,直接把最大堆元素值取负。
二、最大堆实现
2.1 最大堆操作
最大堆(MaxHeap)数据结构实际为完全二叉树,每个结点的元素值不小于其子结点的元素值。
其主要操作有:
- MaxHeap InitializeHeap( int MaxSize ):初始化一个空的最大堆。
- Boolean IsFull( MaxHeap H ):判断最大堆H是否已满。
- Boolean IsEmpty( MaxHeap H ):判断最大堆H是否为空。
- Insert( MaxHeap H, ElementType X ):将元素X插入最大堆H。
- ElementType DeleteMax( MaxHeap H ):返回H中最大元素(高优先级)。
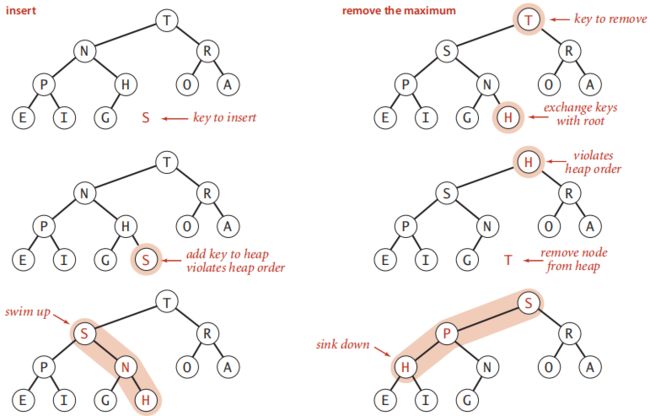
核心操作为 恢复堆序性:在堆中执行了可能违反堆序性的简单修改后,需通过修改堆确保重新满足堆序性。有两种情况:
- 自底向上reheapify(上滤,swim): 当某个节点的优先级增加时(或在堆的底部添加一个新节点)时,必须向上遍历调整堆以恢复堆序。
- 自顶向下reheapify(下滤, sink):当节点优先级减少(变小)时(例如,如果用键较小的新节点替换根上的节点),必须向下遍历调整堆以恢复堆顺。
可以先实现这两个基本辅助操作,然后使用它们来实现插入和删除最大值。其操作如下图所示:
插入-插入元素索引上移,父节点值下移;
删除-孩子节点值上移,末尾元素索引下移(降序插入排序,右边有序,直到找到一个小于它的元素);
2.2 最大堆C实现
2.2.1 基本操作
声明堆结构
#include
#include
typedef int ElementType;
typedef struct HNode *Heap; /* 堆的类型定义 */
struct HNode {
ElementType *Data; /* 存储元素的数组 */
int Size; /* 堆中当前元素个数 */
int Capacity; /* 堆的最大容量 */
};
typedef Heap MaxHeap; /* 最大堆 */
#define MAXDATA 1000000 /* 该值应根据具体情况定义为大于堆中所有可能元素的值 */
初始化堆
MaxHeap InitializeHeap( int MaxSize )
{ /* 创建容量为MaxSize的空的最大堆 */
MaxHeap H = (MaxHeap)malloc(sizeof(struct HNode));
/* 多一个元素存放"哨兵" */
H->Data = (ElementType *)malloc((MaxSize+1)*sizeof(ElementType));
H->Size = 0;
H->Capacity = MaxSize;
H->Data[0] = MAXDATA; /* 定义"哨兵"为大于堆中所有可能元素的值*/
return H;
}
判是否满堆,以及是否为空
bool IsFull( MaxHeap H )
{
return (H->Size == H->Capacity);
}
bool IsEmpty( MaxHeap H )
{
return (H->Size == 0);
}
2.2.2 最大堆的插入
将新增结点插入到,从其父结点到根结点的有序序列中 ( 完全二叉树,插入时间复杂度O(logN) )
一步步往上调整(上滤)
void Insert( MaxHeap H, ElementType X )
{ /* 将元素X插入最大堆H,其中H->Data[0]已经定义为哨兵 */
int i;
/* 首先判断,堆是否已满。已满则结束 */
if ( IsFull(H) ) {
printf("最大堆已满");
return;
}
/* 若堆未满,i指向堆末尾的下一个位置(空穴,当前size+1),准备插入X */
i = ++H->Size; /* 类似插入排序, */
/* 若X 大于 其父节点值,则将父节点值下移至位置i, i位置(空穴)移到父节点位置[i/2] */
for ( ; H->Data[i/2] < X; i /= 2 )
H->Data[i] = H->Data[i/2]; /* 上滤X */
H->Data[i] = X; /* 将X插入 */
/* 若X是当前堆中最大元素,那么会在堆顶时(比哨兵小)终止上移 */
}
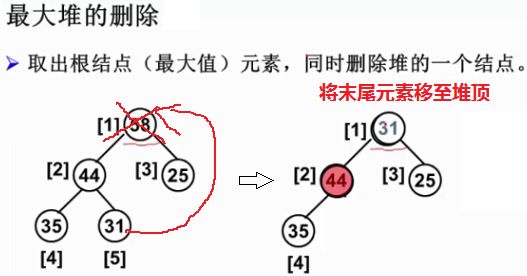
2.2.3 最大堆的删除
删除位置-根结点,返回堆顶(最大值)元素,并调整堆使其保持堆序性(少了一个元素)。
ElementType DeleteMax( MaxHeap H )
{ /* 从最大堆H中取出键值为最大的元素,并删除一个结点 */
int Parent, Child; /* 指针 */
ElementType MaxItem, X;
if ( IsEmpty(H) ) {
printf("最大堆已为空"); /* 若堆已空,则结束(没得删) */
return ERROR;
}
MaxItem = H->Data[1]; /* 取出根结点存放的最大值 */
/* 用最大堆中最后一个元素X,从根结点开始,向上过滤下层结点 */
X = H->Data[H->Size--]; /* 相当于删掉末尾元素位置,故当前堆size要减1*/
/* 迭代地将X和其更大的孩子节点值作比较,并调整位置(从根节点开始,给X找个位置) */
/* Parent*2 <= H->Size判断是否有左儿子(有无孩子),若无则超出堆空间,跳出循环,直接把X放Parent */
for ( Parent = 1; Parent*2 <= H->Size; Parent = Child ) {
/* 找到当前更大的孩子节点*/
Child = Parent * 2; /* 令Child为左儿子,经过外层for循环判断,Child只能 <= Parent */
/* 若有右儿子((Child < H->Size)),则让让Child指向左右子结点的较大者 */
if ( (Child != H->Size) && (H->Data[Child] < H->Data[Child+1]) )
Child++;
/* 将末尾元素X和Child的值比较,若X >= Child值则结束(有序了)*/
/* 若X < Child值 (Child更大),则将Child值放在位置Parent,并将Parent位置移到Child位置 */
if ( X >= H->Data[Child] )
break; /* 找到了合适位置 */
else /* Child元素上移,X移动到下一层(Parent = Child),继续和其孩子节点比较 */
H->Data[Parent] = H->Data[Child];
}
H->Data[Parent] = X;
return MaxItem;
}
自顶向下,找到更大的孩子节点(孩子不一定是2个,也可能只有1个),并和末尾元素比较
若孩子更小或等于则不动,若孩子更大则将孩子值上移。末尾元素索引下移-下滤
2.2.4 最大堆的建立
将已经存在的N个元素,按最大堆的要求存放在一个一维数组中
方法1:通过插入操作,将N个元素一个个相继插入到一个初始为空的堆中去,其时间代价最大为O(N logN)。
方法2:在线性时间复杂度O(N)下,建立最大堆。
- 将N个元素按输入顺序存入,先满足完全二叉树的结构特性
- 调整各结点位置,以满足最大堆的有序特性
分析:该如何调整堆?
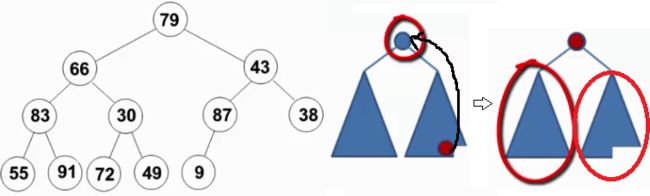
在删除最大值操作中,末尾元素放置于堆顶,此时其左子树和右子树均为堆。其调整思路为,不断地找更大的孩子调上来,自己下沉(下滤操作)。
但是,如上图左子图所示,初始化的堆并不满足堆序性(对79而言,其左右均不是堆,其他节点也是这个情况),似乎不能直接使用删除最大值操作。
实际可以逆向思维,找到最小满足该情况的例子:
从倒数第一个有儿子的节点开始(末尾节点的父亲,此节点的左右肯定是堆-叶节点),逆序执行(自底向上,逆层序遍历)下滤操作。这样 当目标节点的左子树和右子树都为堆时,就可以自然地复用删除最大值操作
void PercolateDown( MaxHeap H, int p )
{ /* 下滤:将H中以H->Data[p]为根的子堆调整为最大堆 */
int Parent, Child;
ElementType X = H->Data[p]; /* 取出根结点存放的值 */
for ( Parent=p; Parent*2<=H->Size; Parent=Child ) {
Child = Parent * 2;
if ( (Child!=H->Size) && (H->Data[Child]Data[Child+1]) )
Child++; /* Child指向左右子结点的较大者 */
if ( X >= H->Data[Child] ) break; /* 找到了合适位置 */
else /* 下滤X */
H->Data[Parent] = H->Data[Child];
}
H->Data[Parent] = X;
}
void BuildHeap( MaxHeap H )
{ /* 调整H->Data[]中的元素,使满足最大堆的有序性 */
/* 这里假设所有H->Size个元素已经存在H->Data[]中 */
int i;
/* 从最后一个结点的父节点开始,到根结点1 */
for ( i = H->Size/2; i > 0; i-- )
PercolateDown( H, i );
}
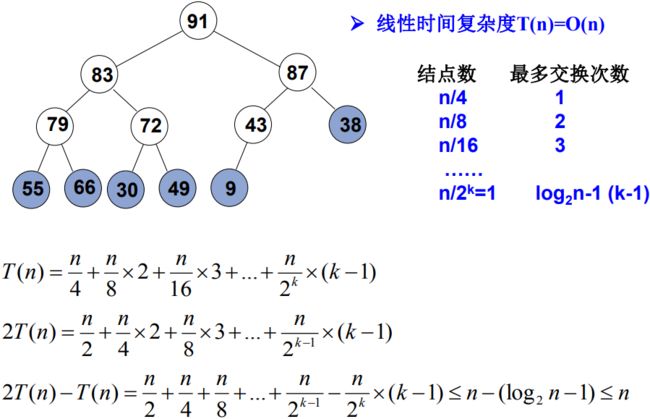
分析
倒数第2层最多交换1次, 其余节点的交换次数此时按其深度线性递增(节点数按2的对数下降)
基于下滤操作的删除最大值实现:
ElementType DeleteMax( MaxHeap H )
{ /* 从最大堆H中取出键值为最大的元素,并删除一个结点 */
ElementType MaxItem = H->Data[1]; /* 取出根结点存放的最大值 */
H->Data[1] = H->Data[H->Size--] /* 取出根结点存放的最大值 */
PercolateDown(H, 1); /* 从根结点开始,向上过滤下层结点(末尾节点下滤) */
return MaxItem;
}
可知,删除最大值中的调整操作是BuildHeap的特例。此外,还有删除堆中某个元素、增大某个元素的优先级和减小某个元素的优先级的操作。高效执行此操作的前提 ,是用哈希表简历key到index的映射。
2.3 最大堆Python实现
逻辑参照上述C语言版
class Heap:
def __init__(self, n):
self.capacity = n
self.size = 0
self.arr = [None] * (self.capacity+1)
self.arr[0] = 2e24
def insert(self, num):
if self.size == self.capacity:
print("Out of size")
else:
self.size += 1
child = self.size # 空穴位置
# 上滤, 当左儿子在堆范围内
while num > self.arr[child // 2]:
parent = child // 2
self.arr[child] = self.arr[parent]
child = parent
self.arr[child] = num
def pop(self):
if self.size == 0:
print("Empty")
else:
max_item = self.arr[1] # 取堆顶
x = self.arr[self.size] # 取堆末尾元素
self.size -= 1
parent = 1
# 下滤, 当左儿子在堆范围内
while parent * 2 <= self.size:
child = parent * 2
if child != self.size and self.arr[child+1] > self.arr[child]:
child += 1
if self.arr[child] > x:
self.arr[parent] = self.arr[child] # 孩子节点值上移
parent = child
else:
break
self.arr[parent] = x
return max_item
调用python包
import queue
, random
class Heap():
def __init__(self, k):
if k > 0:
self.q = queue.PriorityQueue(k)
def queue(self):
return self.q.queue
def enque(self, key):
# 当前堆大小小于其容量
if self.q._qsize() < self.q.maxsize:
self.q.put(key)
else:
self.q.get() # 删除堆顶
self.q.put(key)
def deque(self):
if not self.q.empty():
return self.q.get()
else:
print("Empty heap")
h1 = Heap(10)
for i in range(15):
h1.enque(i)
print(h1.queue()) # 最小堆,k 可得到堆排序得到最大的k个
l1 = [ random.randint(1, 100) for i in range(20)]
print(l1)
for i in l1:
h1.enque(i)
print(h1.queue())
print("\nPriority Queue:")
print([h1.deque() for i in range(h1.q._qsize())])
三、堆的应用
经典的应用有选择问题、堆排序和Huffman编码等等。
3.1. 选择问题
问题描述:输入N个数,找到第k个最大的数。如果K=N/2,就是找中位数, 这是选择问题的最困难的情况。
暴力法:直接排序,并返回排序数组的倒数第K个数,O(NlogN),
使用堆:
算法A: 大优先队列
- 将N个元素读入数组,并构建最大堆O(N)
- 然后执行K次删除最大元素O(KlogN)
最后一次删除的元素就是第K个最大值,总时间复杂度:O(N + KlogN)。
- 如果k小时,运行时间取决于建堆O(N)。
- 如果k大时,运行时间取决于删除O(KlogN)。例如K=N,即O(NlogN),直接堆排序
- 如果K=N/2,平均时间复杂度(NlogN)
算法B: 小优先队列(流式处理)
- 将K个元素读入数组,并构建最小堆O(K)
- 依次删除最小堆的最小元素,再将元素插入最小堆(把待插入元素放在堆顶,然后下滤)O((N-K)logK)
因此,O(K + (N-K)logK) = O(K(1-logK) + NlogK) = O(NlogK)
3.2 堆排序
- 将N个元素读入数组,并构建最大堆O(N) Heap的原理和实现
- 然后,执行N-1次删除最大元素O(NlogN),返回的元素构成的数组有序
每次删除元素可以放在当前堆尾。慢于希尔排序。
- 实际实现时,先自底向上调用N/2 + 1次下滤操作PercolateDown,线性建堆。
- 然后,每次把堆顶元素和堆末尾元素交换,将堆size减1,并从根节点执行下滤操作PercolateDown。共计N-1次(最后一个元素已经在堆顶,不需要操作)
堆排序不完全同于二叉堆的删除,其数组元素初始位置在0,所以下滤开始位置为0而不是1,下滤范围从N-1到1(实际堆的大小)。
Python调包版
def sortArray(nums: List[int]) -> List[int]:
import heapq
heapq.heapify(nums)
return [heapq.heappop(nums) for i in range(len(nums))]
Python实现
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
def heapify(nums, parent, arr_size):
# parent为开始下滤节点索引,p为当前堆大小(决定调整边界)
x = nums[parent]
# 下滤, 当左儿子在堆范围内
while parent * 2 + 1 < arr_size:
child = parent * 2 + 1
if child != arr_size-1 and nums[child+1] > nums[child]:
child += 1
if nums[child] > x:
nums[parent] = nums[child]
parent = child
else:
break
nums[parent] = x
# 构建堆
n = len(nums)
for i in range(n//2, -1, -1):
heapify(nums, i, n) # 建堆时堆大小固定为其容量
# 迭代删除堆顶元素
for i in range(n-1, 0, -1):
# 将堆顶元素取出(直接在末尾存储),把末尾元素放堆顶
nums[i], nums[0] = nums[0], nums[i]
heapify(nums, 0, i) # 然后下滤
return nums
C实现
void PercolateDown( ElementType A[], int p, int N )
{
/* 将N个元素的数组中以A[p]为根的子堆调整为最大堆 */
int Parent, Child;
ElementType X = A[p]; /* 取出根结点存放的值 */
for ( Parent=p; (Parent*2+1) < N; Parent=Child ) {
Child = Parent * 2 + 1;
if ( (Child != N-1) && (A[Child] < A[Child+1]) )
Child++; /* Child指向左右子结点的较大者 */
if ( X >= A[Child] ) break; /* 找到了合适位置 */
else /* 下滤X */
A[Parent] = A[Child];
}
A[Parent] = X;
}
void HeapSort( ElementType A[], int N )
{
int i;
/* 建立最大堆 */
for ( i = N/2-1; i >= 0; i-- )
PercolateDown( A, i, N );
for ( i=N-1; i>0; i-- ) {
/* 删除最大堆顶 */
Swap( &A[0], &A[i] );
PercolateDown( A, 0, i );
}
}
参考资料:算法第四版,浙江大学- 数据结构慕课