深度学习—标准化（Normalization）

前言

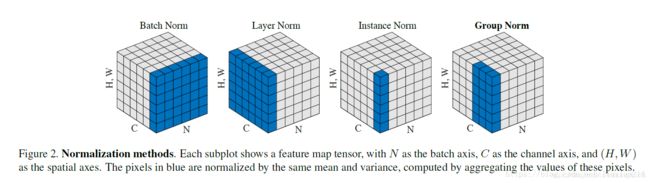
归一化层，目前主要有这几个方法，Batch Normalization（2015年）、Layer Normalization（2016年）、Instance Normalization（2017年）、Group Normalization（2018年）、Switchable Normalization（2018年）；

将输入的shape记为[N, C, H, W]，这几个方法主要的区别就是在：

1. batchNorm是在batch上，对NHW做归一化，对小batchsize效果不好；
2. layerNorm在通道方向上，对CHW归一化，主要对RNN作用明显；
3. instanceNorm在图像像素上，对HW做归一化，用在风格化迁移；
4. GroupNorm将channel分组，然后再做归一化；
5. SwitchableNorm是将BN、LN、IN结合，赋予权重，让网络自己去学习归一化层应该使用什么方法。

下面主要介绍Batch Normalization和Layer Normalization

Batch Normalization

在神经网络中, 数据分布对训练会产生影响. 比如某个神经元 x 的值为1, 某个 Weights 的初始值为 0.1, 这样后一层神经元计算结果就是 Wx = 0.1; 又或者 x = 20, 这样 Wx 的结果就为 2. 现在还不能看出什么问题, 但是, 当我们加上一层激励函数, 激活这个 Wx 值的时候, 问题就来了. 如果使用 像 tanh 的激励函数, Wx 的激活值就变成了 ~0.1 和 ~1, 接近于 1 的部已经处在了 激励函数的饱和阶段, 也就是如果 x 无论再怎么扩大, tanh 激励函数输出值也还是 接近1. 换句话说, 神经网络在初始阶段已经不对那些比较大的 x 特征范围 敏感了. 这样很糟糕, 想象我轻轻拍自己的感觉和重重打自己的感觉居然没什么差别, 这就证明我的感官系统失效了. 当然我们是可以用之前提到的对数据做 normalization 预处理, 使得输入的 x 变化范围不会太大, 让输入值经过激励函数的敏感部分. 但刚刚这个不敏感问题不仅仅发生在神经网络的输入层, 而且在隐藏层中也经常会发生.

只是时候 x 换到了隐藏层当中, 我们能不能对隐藏层的输入结果进行像之前那样的normalization 处理呢? 答案是可以的, 因为大牛们发明了一种技术, 叫做 batch normalization, 正是处理这种情况.

BN 添加位置

Batch normalization 的 batch 是批数据, 把数据分成小批小批进行 stochastic gradient descent. 而且在每批数据进行前向传递 forward propagation 的时候, 对每一层都进行 normalization 的处理

BN效果

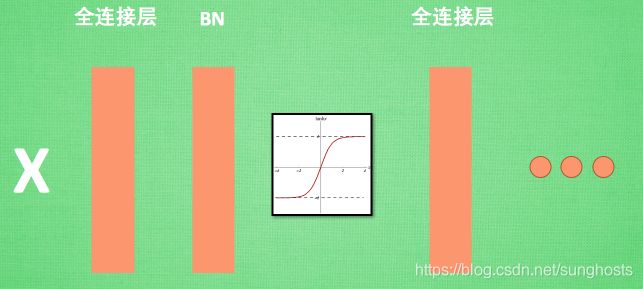
Batch normalization 也可以被看做一个层面. 在一层层的添加神经网络的时候, 我们先有数据 X, 再添加全连接层, 全连接层的计算结果会经过 激励函数 成为下一层的输入, 接着重复之前的操作. Batch Normalization (BN) 就被添加在每一个全连接和激励函数之间.

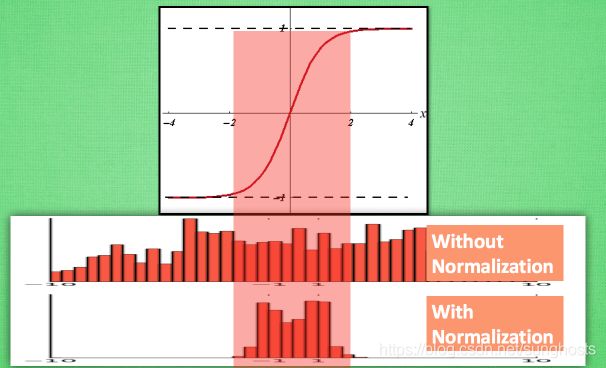
之前说过, 计算结果在进入激励函数前的值很重要, 如果我们不单单看一个值, 我们可以说, 计算结果值的分布对于激励函数很重要. 对于数据值大多分布在这个区间的数据, 才能进行更有效的传递. 对比这两个在激活之前的值的分布. 上者没有进行 normalization, 下者进行了 normalization, 这样当然是下者能够更有效地利用 tanh 进行非线性化的过程.

没有 normalize 的数据 使用 tanh 激活以后, 激活值大部分都分布到了饱和阶段, 也就是大部分的激活值不是-1, 就是1, 而 normalize 以后, 大部分的激活值在每个分布区间都还有存在. 再将这个激活后的分布传递到下一层神经网络进行后续计算, 每个区间都有分布的这一种对于神经网络就会更加有价值. Batch normalization 不仅仅 normalize 了一下数据, 他还进行了反 normalize 的手续. 为什么要这样呢?

BN算法

我们引入一些 batch normalization 的公式. 这三步就是我们在刚刚一直说的 normalization 工序, 但是公式的后面还有一个反向操作, 将 normalize 后的数据再扩展和平移. 原来这是为了让神经网络自己去学着使用和修改这个扩展参数 gamma, 和 平移参数 β, 这样神经网络就能自己慢慢琢磨出前面的 normalization 操作到底有没有起到优化的作用, 如果没有起到作用, 我就使用 gamma 和 belt 来抵消一些 normalization 的操作.

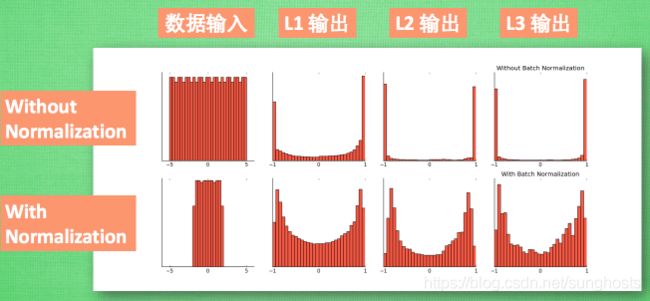
最后我们来看看一张神经网络训练到最后, 代表了每层输出值的结果的分布图. 这样我们就能一眼看出 Batch normalization 的功效啦. 让每一层的值在有效的范围内传递下去.

Layer Normalization

batch normalization存在以下缺点：

• 对batchsize的大小比较敏感，由于每次计算均值和方差是在一个batch上，所以如果batchsize太小，则计算的均值、方差不足以代表整个数据分布；
• BN实际使用时需要计算并且保存某一层神经网络batch的均值和方差等统计信息，对于对一个固定深度的前向神经网络（DNN，CNN）使用BN，很方便；但对于RNN来说，sequence的长度是不一致的，换句话说RNN的深度不是固定的，不同的time-step需要保存不同的statics特征，可能存在一个特殊sequence比其他sequence长很多，这样training时，计算很麻烦。（参考于https://blog.csdn.net/lqfarmer/article/details/71439314）

与BN不同，LN是针对深度网络的某一层的所有神经元的输入按以下公式进行normalize操作。

$$\begin{gathered} {\mu }^l=\frac{1}{H}\sum _{i=1}^H{a}_i^l \\ {\sigma }^l=\sqrt{\frac{1}{H}\sum _{i=1}^H(a_i^l-{\mu }^l{)}^2} \end{gathered}$$

BN与LN的区别在于：

• LN中同层神经元输入拥有相同的均值和方差，不同的输入样本有不同的均值和方差；
• BN中则针对不同神经元输入计算均值和方差，同一个batch中的输入拥有相同的均值和方差。

所以，LN不依赖于batch的大小和输入sequence的深度，因此可以用于batchsize为1和RNN中对边长的输入sequence的normalize操作。

LN用于RNN效果比较明显，但是在CNN上，不如BN。

def ln(x, b, s):
    _eps = 1e-5
    output = (x - x.mean(1)[:,None]) / tensor.sqrt((x.var(1)[:,None] + _eps))
    output = s[None, :] * output + b[None,:]
    return output

参考

https://zhuanlan.zhihu.com/p/24810318

https://blog.csdn.net/liuxiao214/article/details/81037416