【PID优化】基于matlab粒子群算法优化BP神经网络PID控制【含Matlab源码 2022期】
一、粒子群算法优化BP神经网络PID控制简介
BP神经网络PID控制算法
传统PID控制器作为一种线性控制器,具备结构,容易实现的优点,其基本原理是将系统的实际输出值和期望输出值之间的偏差按照比例、积分和微分的形式进行线性组合,构成控制量,实现对目标的反馈控制,控制性能取决于P、I、D 3个参数,然而由于传统PID的控制参数需要根据经验预先设置且不能在线实时调整,因此在面对非平稳时变系统时存在稳定性差、控制精度不理想等问题。
BP神经网络是目前应用最为广泛的一种神经网络模型,作为一种多层前向反馈神经网络,具备并行计算和自适应学习能力,理论上能够以任意精度逼近于非线性函数,因此该文将BP神经网络与传统PID控制器相结合,利用BP神经网络对P、I、D3个参数进行自适应在线调整,从而提高PID系统面对非平稳非线性系统时的稳定性和控制精度。
1 BP神经网络结构
该文采用如图1所示的4-5-3三层BP神经网络结构,图中j、i和l分别对应输入层神经元、中间层神经元和输出层神经元。其中输入层神经元为系统实际输出值、期望输出值、系统偏差和控制量4个变量,输出层神经元为PID控制器的3个参数kP、kI和kD,将中间层神经元个数设置为5。
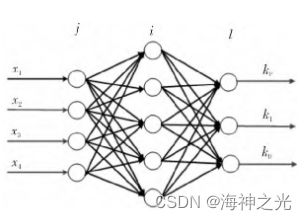
图1 所用三层BP神经网络结构
2 BP-PID控制器
将BP神经网络和PID控制相结合组成的BP-PID控制器结构如图2所示,可以看出其基本思路是将BP神经网络加入到PID控制过程中,根据当前系统的运行状态,利用BP网络的自适应学习能力,实现对PID系统kP、kI和kD3个参数的实时在线调整,然后通过传统PID完成对系统的闭环控制。
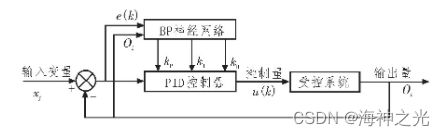
图2 BP-PID控制原理图
根据BP神经网络的输入变量xj,利用Sigmoid函数f ()·可以得到其中间层节点的输入neti(2)(k)和输出Oi(2)(k)为:
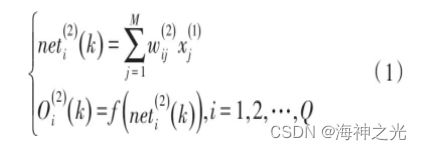
其中,wli(3)为中间层神经元和输出层神经元之间的加权系数,函数h(x)为非负的Sigmoid函数,其具体形式为:

系统实际输出与预期输出之间的偏差为e(k)=Oi-xj,则采用增量式PID控制算法可以计算得到PID控制量的值u(k),对其进行离散化得到的结果如式(4)所示:
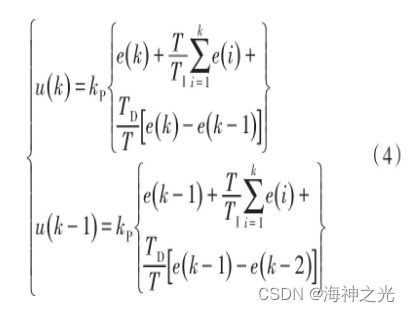
其中,TI和TD分别为积分和微分时间参数。进一步可以得到PID的控制增量,如式(5)所示:
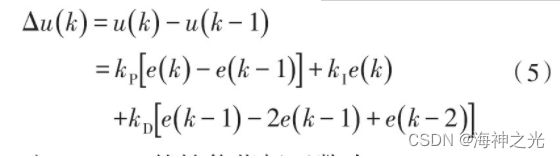
定义BP-PID的性能指标函数为:
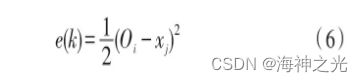
利用梯度下降法对式(6)进行求解,可得模型参数的更新公式,如式(7)所示:

二、部分源代码
clear all;
close all;
xite=0.50;
alfa=0.05;
IN=4; H=5; Out=3;
ts=0.01;
% wi=0.50rands(H,IN);
% wo=0.50rands(Out,H);
%结合粒子群数值优化算法的神经网络权重初始化矩阵
wi=[
-4.7730 5.0000 4.8238 -4.7085
4.9337 4.8659 -4.9651 -4.8618
4.9470 4.9485 -4.6965 4.8327
5.0000 4.9508 4.5696 4.9154
4.6047 -4.7804 5.0000 -4.7332
];
wo=[
4.9438 -4.6610 4.9293 4.7416 -4.9323
5.0000 4.9414 4.0693 -4.7460 5.0000
-4.9147 4.8119 4.9292 4.9434 4.9398
];
%[wi , wo]=SPO_InitW();
wi_init_save=wi; wo_init_save=wo;
wo_1=wo; wo_2=wo;
wi_1=wi; wi_2=wi;
%M=[10,1,10];
%激活函数系数
M=[9.9,9.8,9.4];
x=[0,0,0];
du_1=0;
u_1=0; u_2=0; u_3=0; u_4=0; u_5=0;u_6=0;u_7=0;
y_1=0; y_2=0; y_3=0;
error_1=0; error_2=0;
Oh=zeros(H,1);
I=Oh;
sys=tf(400,[1,50,0]);
dsys=c2d(sys,ts,‘z’);
[num,den]=tfdata(dsys,‘v’);
for k=1:1:200
time(k)=k*ts;
rin(k)=1.0;
yout(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_1+num(3)u_2;
error(k)=rin(k)-yout(k);
X(1)=error(k)-error_1;
X(2)=error(k);
X(3)=error(k)-2error_1+error_2;
xii=[X(1),X(2),X(3),1];
xi=xii/norm(xii);
epid=[X(1);X(2);X(3)];
%%%前向传播----------------------------------------
net2=xi*(wi');
for j=1:1:H
Oh(j)=( exp( net2(j)-exp(-net2(j)) ) )/(exp( net2(j)+exp(-net2(j)) ));
end
net3=wo*Oh;
for l=1:1:Out
K(l)=exp(net3(l))/(exp(net3(l))+exp(-net3(l)));
%K(l)=M*net3(l);
end
kp(k)=M(1)*K(1); ki(k)=M(2)*K(2); kd(k)=M(3)*K(3);
Kpid=[kp(k),ki(k),kd(k)];
du(k)=Kpid*epid;
u(k)=u_1+du(k);
if u(k)>10
u(k)=10;
end
if u(k)<-10
u(k)=-10;
end
%%%后向传播------------------------------------------------
dyu(k)=sign((yout(k)-y_1)/(du(k)-du_1+0.0001));
for j=1:1:Out
dK(j)=1/(exp(net3(j))+exp(-net3(j)));
%dK(j)=M;
end
for l=1:1:Out
delta3(l)=error(k)*dyu(k)*epid(l)*dK(l);
end
for l=1:1:Out
for i=1:1:H
d_wo=xite*delta3(l)*Oh(i)+alfa*(wo_1-wo_2);
end
end
wo=wo_1+d_wo+alfa*(wo_1-wo_2);
%更新M系数
% for h = 1:Out
% dM(h)=error(k)K(h);
% M(h)=M(h)+ritedM(h);
% end
for i=1:1:H
dO(i)=4/(exp(net2(i))+exp(-net2(i)))^2;
end
segma=delta3*wo;
for i=1:1:H
delta2(i)=dO(i)*segma(i);
end
d_wi=xite*delta2'*xi;
wi=wi_1+d_wi+alfa*(wi_1-wi_2);
wo_2=wo_1; wo_1=wo;
wi_2=wi_1; wi_1=wi;
du_1=du(k);
u_7=u_6;u_6=u_5;u_5=u_4; u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k);
y_2=y_1; y_1=yout(k);
error_2=error_1; error_1=error(k);
end
figure(2);
[t,y]=BPNN_PID();
plot(t,y,‘g’,‘Linewidth’,2);
hold on;
plot(time,rin,‘r’,‘Linewidth’,2);
xlabel(‘t/s’); ylabel(‘rin,yout’);
hold on ;
plot(time,yout,‘c’,‘Linewidth’,2);
hold on;
[x,y]=classic_PID();
plot(x,y,‘b’,‘Linewidth’,2);
%-----------------
figure(3);
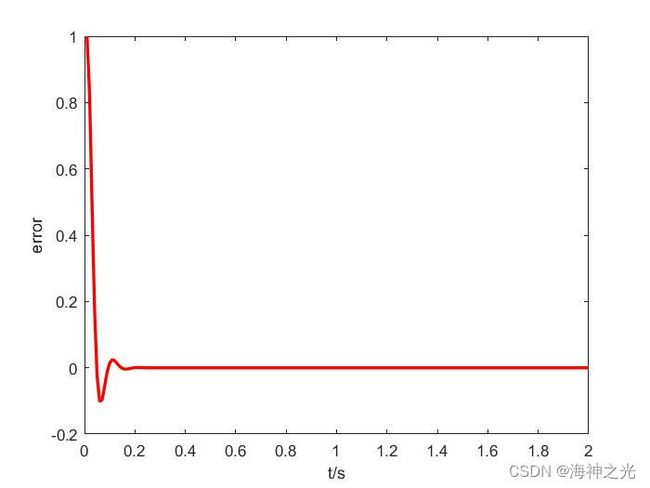
plot(time,error,‘r’,‘Linewidth’,2);
xlabel(‘t/s’); ylabel(‘error’);
figure(4);
plot(time,u,‘r’,‘Linewidth’,2);
xlabel(‘t/s’); ylabel(‘u’);
figure(5);
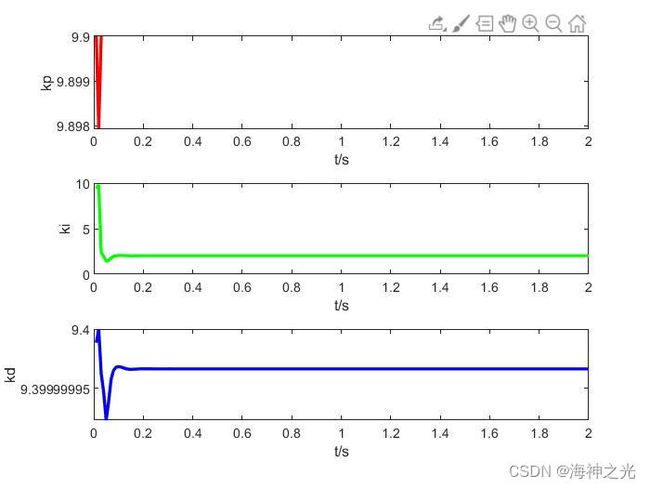
subplot(311);
plot(time,kp,‘r’,‘Linewidth’,2);
xlabel(‘t/s’); ylabel(‘kp’);
subplot(312);
plot(time,ki,‘g’,‘Linewidth’,2);
xlabel(‘t/s’); ylabel(‘ki’);
subplot(313);
plot(time,kd,‘b’,‘Linewidth’,2);
xlabel(‘t/s’); ylabel(‘kd’);
三、运行结果
四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除