计算机视觉与机器人控制：基础概述

Thanks Mark W. Spong for his great work of Robot Modelling and Control.

相机外部参数与内部参数

相机坐标系与像素坐标系

为简化公式，用以相机为中心的坐标系来表示物体坐标是十分有效的。因此，定义相机坐标系如下：包含检测阵列的平面定义为图像平面；轴线 xc 和 yc 组成图像平面的坐标基，轴线 zc 垂直于图像平面且与光轴对准，即它穿过镜头的焦点；相机坐标系的原点位于图像平面后距离为一个焦距 λ 的位置；该店被称为投影中心 （center of projection）；光轴与图像平面的交点被称为主点（principal point）。

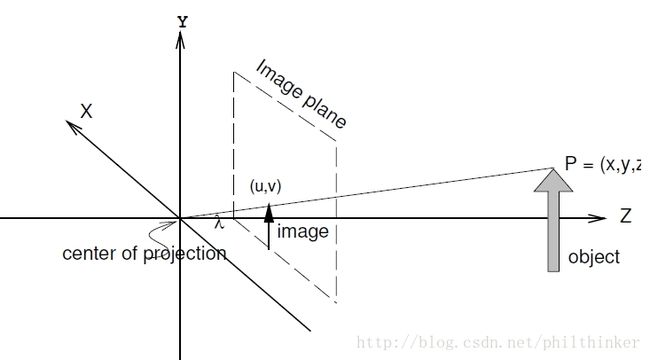
图像平面中的任何一点都将具有坐标 (u,v,λ) ，我们用 (u,v) 来指代图像平面坐标（image plane coordinate）。令 P 表示相对于相机参考系坐标为 (x,y,z) 的一个点，令 p 表示 P 在图像平面内的投影，其坐标为 (u,v,λ) 。在针孔模型假设下：

k⎛⎝⎜xyz⎞⎠⎟=⎛⎝⎜uvλ⎞⎠⎟

即：

u=λxz,v=λyz

这些被称为 透视投影方程（perspective projection）。

图像是一个离散的灰度值阵列，我们使用 (r,c) 来表示一个像素的行索引和列索引。下面我们确定平面坐标 (u,v) 和像素坐标 (r,c) 之间的关系。像素坐标系的原点通常被取在图像的边角处，使用 (or,oc) 来表示包含主点的像素的像素坐标。一般情况下感测元件不具有单位尺寸也未必是正方形。使用 sx 和 sy 来分别表示一个像素在水平和垂直两个方向上的尺度。由于我们通常将相机投影中心放在图像后方，像素阵列的水平和垂直轴线与相机坐标系的水平和垂直轴线方向往往相反。基于以上描述，我们得到：

−usx=(r−or),−vsy=(c−oc)

这种关系仅是一种近似，由于像素坐标是整数，现实中可以四舍五入。

外部参数

下面我们推导如何让某一点 P 的坐标 (x,y,z) 与其在图像中的像素坐标 (r,c) 联系起来，这叫做相机的标定。在典型的机器人应用中，任务往往是相对于世界坐标系进行表达的，如果知道了相机坐标系相对于世界坐标系的位置和姿态，我们有：

xw=Rwcxc+Owc

或者说：

xc=Rcw(xw−Owc)

方便起见，我们定义：

R=Rcw,T=−RcwOwc

那么

xc=Rxw+T

其中 R 和 T 一起被称为相机的 外部参数（extrinsic camera paramter）。

内部参数

从世界坐标系到像素坐标系可以通过以下公式得到：

r=−λsxxz+or,c=−λsyyz+oc

也就是说，一旦知道了 λ,sx,or,sy,oc 的取值，我们就可以由 (x,y,z) 确定 (r,c) ，其中 (x,y,z) 是相对于相机参考系的。事实上，如果知道以下比率:

fx=λsx,fy=λsy

就可以不需要 λ,sx,sy 。 参数 fx,or,fy,oc 被称为相机的 内部参数（intrinsic camera parameter），对于一个相机，这些参数是常数。

图像中物体的位置和方向

下面我们介绍如何根据图像得到被操作物体的位置和方向。

图像矩

图像矩是定义在图像上的函数，用来描述图像中物体的形状大小等信息，对于图像中的第 k 个物体， 其 i,j 矩记作 mij(k) ，定义如下：

mij(k)=∑r,cricjIk(r,c)

其中 Ik 是 指示函数（indicator function）定义如下：

Ik(r,c)={1像素 (r,c) 包含在区域 k 内0其它情况

那么，可以看出， m00 等于物体中像素的数目。图像矩的阶被定义为 i+j 。

质心和中心矩

计算一个物体的质心时，一阶矩十分有用：

m10(k)=∑r,crIk(r,c),m01(k)=∑r,ccIk(r,c)

物体的位置由 质心（centroid）定义。一个物体的质心为坐标等于 (r¯,c¯) 的点，并满足以下条件：如果一个物体的所有质量集中在点 (r¯,c¯) 处，其一阶矩保持不变。因此，我们有：

∑r,cr¯iIi(r,c)=∑r,crIi(r,c)⇒r¯i=∑r,crIi(r,c)∑r,cIi(r,c)=m10(i)m00(i)

∑r,cc¯iIi(r,c)=∑r,ccIi(r,c)⇒c¯i=∑r,ccIi(r,c)∑r,cIi(r,c)=m01(i)m00(i)

我们可以相对于物体的质心来计算图像矩，通过这种方式，我们可以得到某些不随物体平移而变化的特征。这些图像矩被称为 中心矩。第 k 个物体的 i,j 阶中心矩定义如下：

Cij(k)=∑r,c(r−r¯k)i(c−c¯k)jIk(r,c)

物体的方向

我们将图像中某个物体的方向定义为穿过该物体轴线的方向，此时使得物体关于轴线的二阶矩最小。这个轴线是最小惯量轴线的二维等价。对于图像中一条给定的直线，物体关于该线的二阶矩定义如下：

L=∑r,cd2(r,c)I(r,c)

其中 d(r,c) 是坐标为 (r,c) 的像素距离该直线的最小距离。尽可能减小 λ 才能够使我们找到最小惯量轴线，为此，我们使用直线的 ρ,θ 参数化：

xcosθ+ysinθ−ρ=0

可以看出 (cosθ,sinθ) 给出了对应直线的单位垂向量，同时 ρ 给出了原点到该直线之间的垂直距离。那么：

d(r,c)=xcosθ+ysinθ−ρ

L 的最小值 L∗ 由下式给出：

L∗=minρ,θ∑r,c(xcosθ+ysinθ−ρ)2I(r,c)

这里省略求最小值的步骤——用梯度即可，且穿过质心的直线使得惯量最小——只给出结果：

∂∂ρL=−2m00(r¯cosθ+c¯sinθ−θ)∂∂ρL=−(C20−C02)sin2θ+2C11cos2θ

最终我们可以得到：

tan2θ=2C11C20−C02

基于图像的视觉伺服控制

基于视觉的控制所面临的问题是：从图像中提取出相关且鲁棒的参数集，用来实时控制机械臂运动。对于相机的选择问题，我们只考虑带有固定焦距镜头的单个相机系统。

首先我们需要确定在哪里放置相机，相机可以放置在一个固定的位置，也可以连接到机器人上，这些方案分别被称为固定相机位形（fixed camera）和手眼相机位形（eye-in-hand）。在固定相机位形中，由于视场不改变，即相机与工作空间之间的几何关系固定，并且可以通过离线标定确定这种关系。然而，当机械臂在工作空间移动时，可能会遮住相机的视场，这对于有高精度需求任务的影响十分严重。在手眼位形中，相机可以不受遮挡地观察末端执行器的运动。然而，相机与工作空间的几何关系随着机械臂的运动而发生改变。下面我们既考虑手眼相机位形。

解决基于视觉的控制问题有两种方法，区别在于如何使用视觉系统所提供的数据。第一种被称为基于位置的视觉伺服控制（position-based visual servo control）。其中，视觉数据被用于构建关于世界的部分三维表示。该方法的难点在于实时建立三维描述。特别是，这些方法相对于相机标定误差的表现并不鲁棒。此外，该方法也没有对图像本身的直接控制。因此，基于位置的各种方法的一个共同问题是：相机的运动可能使用户感兴趣的对象离开视场。
第二种方法被称为基于图像的视觉伺服控制（image-based visual servo control）。它直接使用图像数据来控制机器人运动。使用直接在图像中测量的量来定义一个误差函数，同时建立一个控制律来将误差直接映射到机器人运动中。最常见的方法是使用物体上易检测的点作为特征点。下面我们仅考虑基于图像的视觉伺服控制方法。

交互作用矩阵

图像特征向量与相机速度之间的关系式线性子空间之间的一个线性映射，我们将对这个概念进行严格解释。令 s(t) 表示图像中的一个可测量的特征值向量，其导数 s˙(t) 被称为图像特征速度（image feature velocity）。对于图像中的单点：

s(t)=(u(t)v(t))

在这种情况下， s˙(t) 是点在图像平面内的速度。图像特征速度与相机速度之间有线性关系，令 相机速度 ξ 由线速度 v 和角速度 w 组成

ξ=(vw)

从而使得相机参考系的原点的线速度为 v ，同时相机坐标系围绕闯过相机坐标系原点的轴线 w 旋转。那么：

s˙=L(s,q)ξ

L(s,q) 被称为 交互作用矩阵（interaction matrix）也被称为 图像雅克比矩阵（image Jacobian matrix）。其具体形式取决于用于定义 s 的特征。最简单的特征是图像中的点坐标。这里不给出具体推导过程，仅展示结果。
对于移动的相机观察空间中某一固定点这样的情形：

p˙c=−wc×pc−o˙c

P 为空间中任一点，令其相对于相机参考系的坐标为 pc=(x,y,z)T ，使用本约定，点 P 相对于移动相机参考系的速度正好为 p˙c=(x˙,y˙,z˙)T 。我们将角速度向量坐标表示为 wc=(wx,wy,wz)T 。指定坐标 RTo˙=(vx,vy,vz)T=o˙c 。进而：

⎛⎝⎜x˙y˙z˙⎞⎠⎟=−⎛⎝⎜wxwywz⎞⎠⎟×⎛⎝⎜xyz⎞⎠⎟−⎛⎝⎜vxvyvz⎞⎠⎟

(u˙v˙)=⎛⎝⎜⎜⎜−λz00−λ2uzvzuvλλ2+v2λ−λ2+u2λ−uvλv−u⎞⎠⎟⎟⎟⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜vxvyvzwxwywz⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟

该式中的矩阵是一个点的交互作用矩阵， 即：

s˙=Lp(u,v,z)ξ

上式可被分解为：

s˙=Lv(u,v,z)v+Lw(u,v)w

ξ 有6个自由度，然而只有 u 和 v 可以在图像中观察到。因此，并非所有的相机运动都会在图像中引起可观察到的变化。 L∈R2×6 因此它的归零空间的维度为4。因此系统 0=L(s,q)ξ 在 R6 的4维子空间或者单点情况下具有解向量 ξ 。 可以证明，该归零空间由4个向量生成：

⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜uvλ000⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟,⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜000uvλ⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟,⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜uvz−(u2+λ2)zλvz−λ20uλ⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟,⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜λ(u2+v2+λ2)z0−u(u2+v2+λ2)zuvλ−(u2+λ2)zuλ2⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟

上述交互作用矩阵可以直观地被推广到多点情形：

s=⎛⎝⎜⎜⎜⎜⎜⎜⎜u1v1⋮unvn⎞⎠⎟⎟⎟⎟⎟⎟⎟,z=⎛⎝⎜⎜z1⋮zn⎞⎠⎟⎟

Lc(s,z)=⎛⎝⎜⎜L1(u1,v1,z1)⋮Ln(un,vn,zn)⎞⎠⎟⎟

基于图像的控制律

对于基于图像的控制，其目标位形通过图像特征的目标位形来定义，标记为 sd 。那么，图像误差函数由下式给出：

e(t)=s(t)−sd

在基于图像的控制中，最常用的方法是计算期望的相机速度 ξ ，并将它作为控制输入。图像特征速度到相机速度的联系可通过求解交互作用来完成。在一些情况下可以通过简单地对交互作用矩阵求逆来完成，但是一些情况下必须使用伪拟矩阵。

相机的运动

对于具有 k 个特征且相机速度 ξ 具有 m 个分量的情形，我们有 L∈Rk×m 。通常 m=6 但是某些情况下 m<6 。对此，计算相机的运动必须分情况讨论。

1. 当 k=m 且矩阵 L 满秩时，ξ=L−1s˙ 。
2. 当 k<m 时，此时 L−1 不存在，系统是欠约束的。在这种情况下，我们无法观察的足够的特征速度以确定唯一的的相机运动 ξ 。这种情况下，我们可以借助伪拟给出解答：
   ξ=L+s˙+(Im−L+L)b
   其中 L+=LT(LLT)−1 ， b∈Rm 是任意向量。
3. 当 k>m 且矩阵 L 满秩时，我们通常将会得到一个不一致的系统。在视觉伺服应用中，这意味着我们观察到比唯一确定的相机速度 ξ 所需更多的特征速度。在这种情况下，我们可以使用最小二乘解：
   ξ=L+s˙
   其中伪拟矩阵由下式给出
   L+=(LTL)−1LT

比例控制器

回忆之前对于相机速度与特征速度的描述：

s˙=L(s,q)ξ,e(t)=s(t)−sd

许多现代的机器人控制器可以以速度 xi 为控制输入，即 u(t)=ξ 。我们定义比例控制律：

u(t)=−KL+e(t)

其中 K∈Rm×m 是对角、正定增益矩阵。为证明其有效性，对误差求导：

e˙(t)=ddt(s(t)−sd)=s˙(t)=Lξ=−KLL+e(t)

当 k=m 且 L 满秩时，那么我们得到：

e˙(t)=−Ke(t)

由于 K 的正定假设，我们可知此时该系统是稳定的。
当 k>m 时，系统稳定的充分条件是矩阵的积 KLL+ 是正定的，这可利用李雅普诺夫方法证明，此处从略。

由于依赖深度信息，我们往往无法知晓 L 或 L+ 的准确值。此时，我们可以使用估计 L^+ 来代替，即 u(t)=−KL^+e(t) 。