多元线性回归：R语言的有关基础操作

数据来源：波士顿地区房价预测完整数据集（CSV格式）_weixin_51454889的博客-CSDN博客

 参考书目：《R语言实战》

（其实我不太清楚实际回归时各种检查和操作的一个整体，因而本篇内容很混乱，主要以介绍对应方法的R语言代码为主）

目录

一、数据集介绍

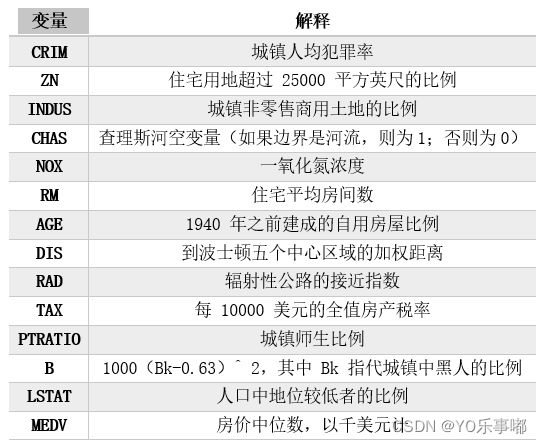
1.1各个属性介绍

1.2描述性统计

二、基础回归

2.1高斯马尔可夫假定：G-M假定

2.2基本模型：OLS估计

2.3GLS估计

三、异常点检验+影响分析

3.1离群点

3.2高杠杆值点

3.3强影响点（影响分析）

3.4整体检测

四、模型基本检查

 4.1多重共线性

4.1.2岭回归

4.2变量选择

4.2.1AIC准则逐步回归

4.2.2全自集回归

五、回归诊断（残差检验）

5.1.正态性检验：

5.2.独立性检验（自相关）*

5.3.线性性：

5.4.同方差性检验（异方差）*

b.box-cox变换

c.加权最小二乘法（特殊的广义最小二乘）

六、实证部分

---

一、数据集介绍

1.1各个属性介绍

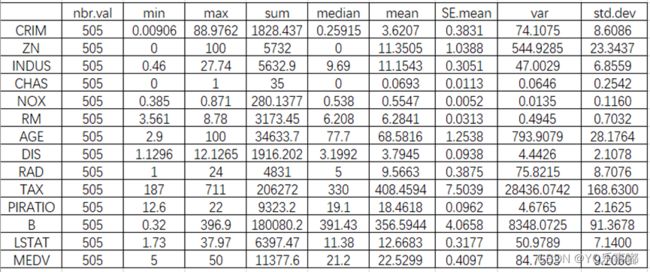
 1.2描述性统计

>stat.desc(df)

library(pastecs)#描述性统计
des_stat<-stat.desc(df)
#输出为csv文件
write.table(des_stat,"描述性统计.csv",sep=",")
#sep：分隔符，默认为空格，则所有数据会在一个单元格里，因此要使用sep","
#row.names：是否导出行序号，默认为TRUE，也就是导出行序号
#col.names：是否导出列名，默认为TRUE，也就是导出列名
#quote：字符串是否使用引号表示，默认为TRUE，也就是使用引号表示

二、基础回归

2.1高斯马尔可夫假定：G-M假定

只有当G-M假定成立时，OLS的估计结果才是最佳线性无偏估计（BLUE：线性性、无偏性、方差最小、一致有效。（上图中可能有误，G-M假定实际应该是前三个假定（？））

2.2基本模型：OLS估计

>lm(y~x1+x2+……)

fit<-lm(Murder~Population+Illiteracy+Income+Frost,data=states)
summary(fit)

 2.3GLS估计

（GLS估计并不是基准回归，但后期会经常用到，故在此介绍）

适用范围：通常当误差项不满足“球形扰动项假设”（即G-M假定中的同方差假定、无自相关假定）时，可以使用GLS估计。

>GLS原理：（广义最小二乘法）

· glm(y~x1+x2+……)

fit_gls=glm(Murder~Population+Illiteracy+Income+Frost,data=states)
summary(fit_gls)

三、异常点检验+影响分析

 3.1离群点

模型预测效果不佳的观测点（通常有很大的正或负的残差）

判断方法：1.Q-Q图 残差落在置信区间外； 2.粗糙判断：学生化残差的绝对值大于2。

· outlierTest(fit)：该函数只检验标准化残差最大的那个点，其他的仍然需要进一步检测）

· influencePlot(fit)：纵坐标提供学生化残差进行判断

3.2高杠杆值点

指x中的不合群点

判断方法：帽子统计量，若观测点的帽子值大于帽子均值的2~3倍则认为是高杠杆值点；

· hatvalues(fit)

hat.plot <- function(fit) {
  p <- length(coefficients(fit))
  n <- length(fitted(fit))
  #hatvalues(fit)是计算fit中每个因变量的帽子统计量
  plot(hatvalues(fit),main = "Index Plot of Hat Values")
  abline(h=c(2,3)*p/n,col="red",lty=2)
  identify(1:n,hatvalues(fit),names(hatvalues(fit)))
}
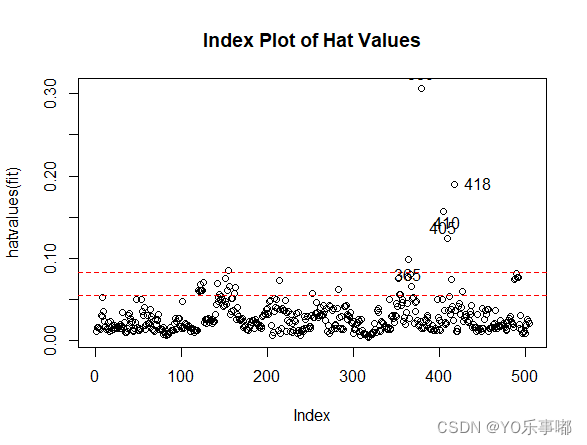
hat.plot(fit)

检验结果显示：365、380、405、410、418属于高杠杆值点

3.3强影响点（影响分析）

（影响分析实际属于回归诊断的内容，放在此处是为了方便三种异常点对比分析）

强影响点：对模型的参数估计值影响巨大，造成比例失衡的点；

判断标准：cook距离，一般Cook‘sD值大于4/(n-k-1)则认为是强影响点；

· cook.distance()可以得到cook距离

cutoff <- 4/(nrow(df)-length(fit$coefficients)-2)
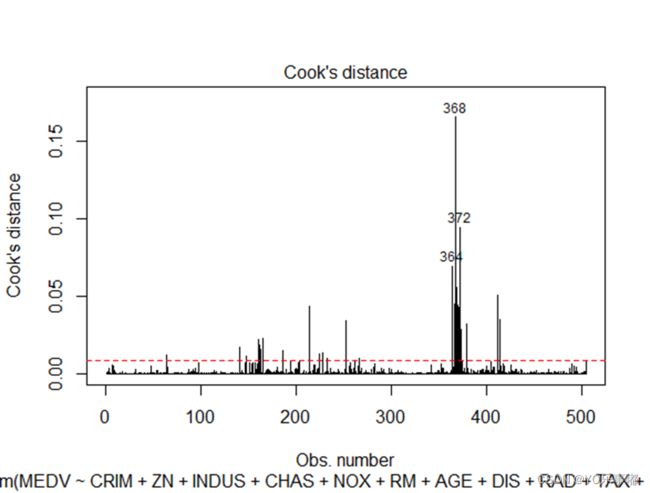
plot(fit, which = 4, cook.levels = cutoff)
abline(h=cutoff,lty=2,col="red")

 我们可以看到自动识别出了364、368、372属于强影响点。

3.4整体检测

· influencePlot()

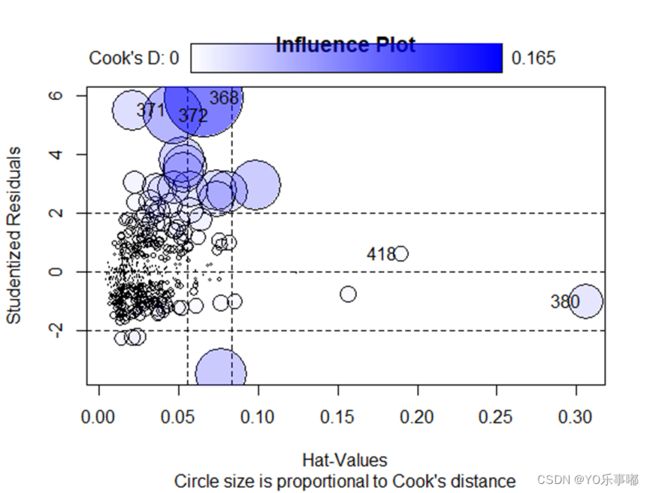
influencePlot(fit,id.method="identify",main="Influence Plot",
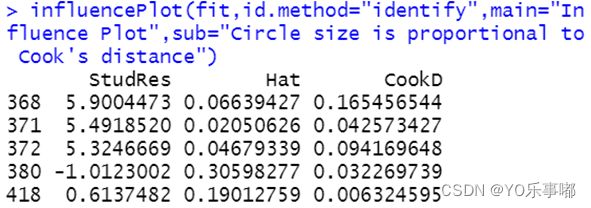
            sub="Circle size is proportional to Cook's distance")

输出结果的图片中：纵坐标代表学生化残差（离群点），横坐标代表帽子统计量（高杠杆值点），指标的圆圈代表影响程度（强影响点）。所以纵坐标超过+2或小于-2的样本点可被认为是离群点，水平轴超过0.2或0.3的样本点为高杠杆值，圆圈的大小与影响成正比。圆圈很大的点可能是对模型参数的估计造成的不成比例影响的强影响点。

该函数自动识别出的异常点结果如上表。

3.5删除异常点，将上述异常点删除再进行后续操作。

四、模型基本检查

 4.1多重共线性

 4.1.1检验方法

1.相关系数矩阵直观判断（粗糙）：cor()

round(cor(states),3) #保留三位数

2.特征根法：若X'X存在一个很小的特征根则认为存在复共线性。

3.方差扩大因子法

 一般认为VIF>10有严重的多重共线性，sqrt(VIF)>2则认为存在多重公共线性问题；

· vif()

#判断多重共线性
vif_judge<-function(fit0){
  vif(fit0)
  sqrt(vif(fit0))>2
}
vif_judge(fit)

本实验数据检验结果显示，可以认为不存在影响严重的多重共线性；

4.1.2岭回归

参考文章：机器学习--线性回归2（共线性问题、岭回归、lasso算法）_zsffuture的博客-CSDN博客

理论原理：（本质意义）对于X’X施加一个惩罚项，使其不再无限接近于0，当k=0时为普通OLS。

lambda应当取多少是未知的，所以要进行迭代，选择合适的lambd使得各个估计的结果趋于平稳，即找到一个最小的lambda，岭迹图中各参数对应的纵坐标不再有较大改变。

岭迹图：纵坐标--估计的beta值，横坐标--lambda；

library(MASS)
#岭回归
gr<-lm.ridge(MEDV~ CRIM+ZN+INDUS+CHAS+NOX+RM+AGE+DIS+RAD+TAX+PIRATIO+B+LSTAT,
             data=df1,
             lambda=seq(0,100,0.01))
#绘制岭迹图
#法一：plot(gr,data =df1,lambda = seq(0,100,0.01))
#法二：
matplot(gr$lambda,t(gr$coef),type='l',
        xlab=expression(lambda),
        ylab=expression(hat(beta)),
        main ='Ridge trace Map')
#选出合适的lambda
select(gr)

输出岭迹图如下：显然本题所用数据不太具有多重共线性，当lambda较小时，其变化对参数估计值几乎没有任何影响（如果具有严重多重共线lambda=0时，估计参数的绝对值应该非常大，且对lambda的变化较为敏感，随着其变化而逐步减小再趋于稳定）。所以本例子中的数据和模型(1)并不适用于岭回归。

其他解决多重共线性问题的还有主成分分析法（待补充）、偏最小二乘法（待补充）

4.2变量选择

4.2.1AIC准则逐步回归

stepAIC(fit1,direction="backward")

4.2.2全自集回归

（其他几个变量选择和模型比较的标准：AIC准则逐步回归、Cp准则、修正的R^2、RMSq）

全自集回归方法当中所有可能的模型都会被检验，分析可以选择展示所有可能的结果。从中选择修正的可决系数最大的那个模型。

library(leaps)
leaps<-regsubsets(MEDV~ CRIM+ZN+INDUS+CHAS+NOX+RM+AGE+DIS+RAD+TAX+PIRATIO+B+LSTAT,
                  data=df1,nbest=14)
#nbset代表展示n个不同子集大小的最佳模型
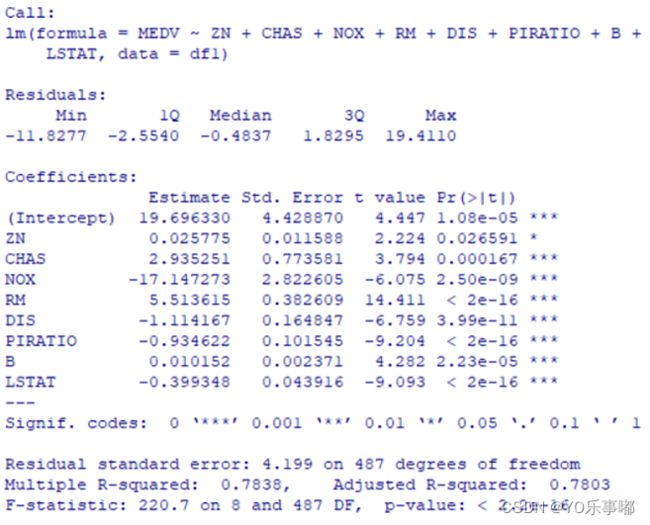
plot(leaps,scale="adjr2")

全自集回归结果显示剔除掉了CRIM、INDUS、AGE、RAD、TAX，建立的最佳模型为MEDV~ZN+CHAS NOX+RM+DIS+PIRATIO+B+LSTAT，此时修正的可决系数达到最大0.78左右，同时因为删除了VIF值较大的几个指标，减轻了复共线性影响。

新模型回归结果如下图所示：此时，所有参数的回归系数p值都显著。

五、回归诊断（残差检验）

OLS回归诊断目的：1.诊断OLS回归统计对残差的基本既定（主要检查残差的正态性、独立性、线性、同方差性）2.影响分析：探究有无强影响点（详见第三节内容）

参考文章：线性回归模型（最小二乘法模型）诊断--R语言_小白15138的博客-CSDN博客

（几乎就是《R语言实战》的回归诊断部分）（由于本题变量过多，所以先进行了多重共线性检验和变量选择，目前仅剩下部分自变量）

  基础方法：

fit<-lm(MEDV~ CRIM+ZN+INDUS+CHAS+NOX+RM+AGE+DIS+RAD+TAX+PIRATIO+B+LSTAT,
        data=df)
par(mfrow=c(2,2))
plot(fit)
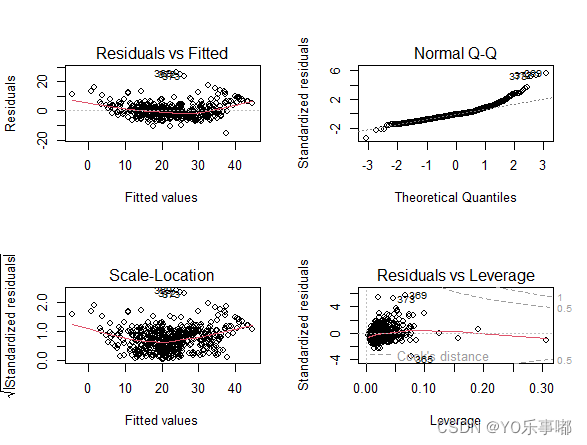
#自动绘制出：残差拟合图、标准化残差Q-Q图、位置尺度图、残差与杠杆图

以上四个图为：残差拟合图（左上-线性）、标准化残差Q-Q图（右上-正态性）、位置尺度图（左下-同方差性）、残差与杠杆图（右下-异常值问题）；

由残差拟合图（左上）可以粗糙看出残差和拟合值具有一定关系，证明模型内还需要对一些数据做变换；标准化残差Q-Q图（右上）几乎近似都在对角线附近分布，可以粗糙认为符合正态性假定；

注：该方法整体比较粗糙，可以按照下述方法进行更为细致的检验。

5.1.正态性检验：

检验方法：

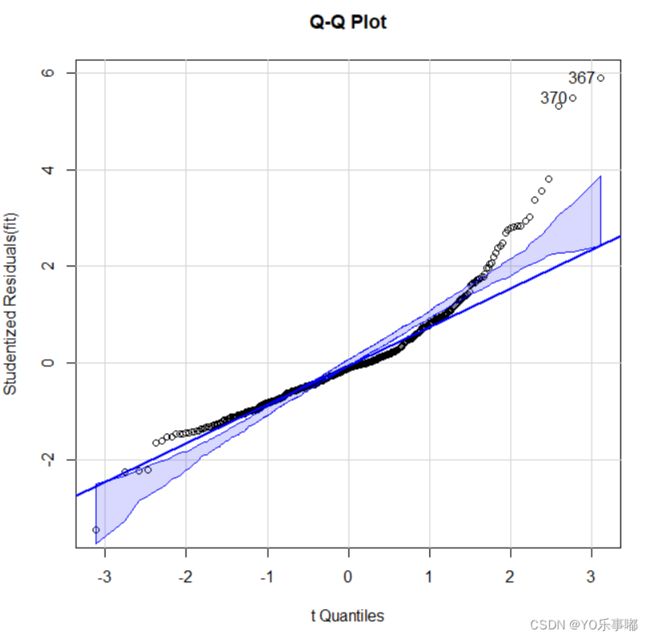
a.学生化残差的正态Q-Q图（含置信区间）

dev.new()
qqPlot(fit,labels=row.names(df),id.method="identify",simulate=TRUE,main='Q-Q Plot')
#simulate=TRUE：自动生成95%置信区间

自动鉴别出367与370两个比较异常的情况。

b.学生化残差：绘制学生化残差直方图拟合曲线，与标准正态分布曲线对比

residplot <- function(fit,nbreaks=10) {
               #生成学生化残差
                z <- rstudent(fit)
                #绘制学生化残差的直方图
                #参数freq=FALSE使得直方图生成的是频率图而不是频数图
                hist(z,breaks=nbreaks,freq=FALSE,
                     xlab="Studentized Residual",
                     main="Distribution of Errors")
                 #绘制轴须图
                rug(jitter(z),col="brown")
                #curve函数常用于绘制函数对应的曲线，确定函数的表达式，以及对应的需要展示的起始坐标和终止坐标，curve函数就会自动化的绘制在该区间的函数图像
                #如果参数add=TRUE,这时图像将在一个已经存在的图像上生成，这种情况下就可以不指定起始和终止坐标
                curve(dnorm(x,mean=mean(z),sd=sd(z)),add=TRUE,col="blue",lwd=2)
                lines(density(z)$x,density(z)$y,col="red",lwd=2,lty=2)
                legend("topright",legend=c("Normal Curve","Kernel Density Curve"),
                       lty=1:2,col=c("blue","red"),cex=.7)
}
residplot(fit)

#————————————————
#版权声明：本文为CSDN博主「小白15138」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出
#处链接及本声明。
#原文链接：https://blog.csdn.net/weixin_42712867/article/details/99815449

5.2.独立性检验（自相关）*

模型的误差项之间具有自相关性。

 >自相关检验方法：

a.观察残差图；b.DW检验（仅能检验一阶自相关，原假设为pho=0）

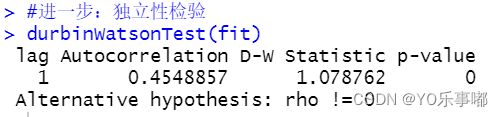
· durbinWatsonTest(fit)

显然p值显著，应当拒绝原假设，则认为误差项之间是不互相独立的，具有自相关性； 

修正方法：广义最小二乘法；迭代法等。

5.3.线性性：

成分残差图/偏残差图来查看是否符合设定；残差为纵轴，拟合值的横轴；二者理论上没有任何关系，若具有关系，则可能需要在模型中加入二次项等进行改进。

· crPlots(fit)

 

由上图可以看出，RM与MEDV可能存在二次项相关，LSTAT与MEDV可能存在倒 数相关，其他的变量与MEDV的相关程度不明显。所以重新建立回归模型，在原有模型基础上添加RM^2与1/LSTAT两项，得到如下模型：

5.4.同方差性检验（异方差）*

若违反了同方差假定，则var(ei)=sigmai^2，随着i的变化而变化，而不再是一个不变的常数。

>异方差检验方法：

1.绘制散点图进行观察

2.G-Q检验：对样本数据从小到大排序（多维时，对高维数据排序可以使用主成分的方法），分为三个部分去掉中间部分，假设高和低的观测值具有同方差性，假设其方差分别为sigma_l^2和sigma_h^2

>异方差修正方法：a.两边取对数来缓解；b.Box-Cox变换；c.加权最小二乘法

b.box-cox变换

参考文章：BOX-COX变换（R语言）_大白羊_Aries的博客-CSDN博客_boxcox变换r语言

#解决方案一：box-cox变换
library(MASS)
bc<-boxcox(MEDV~ZN+CHAS+NOX+RM+DIS+PIRATIO+B+LSTAT,data=df1,lambda=seq(-2,2,0.01))
# λ的取值为区间[-2,2]上步长为0.01的值，bc中保存了λ的值及其对应的对数似然函数值
lambda<-bc$x[which.max(bc$y)]  # 将使对数似然函数值达到最大的λ复制给lambda
lambda
y_bc<-(df1$MEDV^lambda-1)/lambda  # 计算变换后的y值
lm_bc<-lm(y_bc~ZN+CHAS+NOX+RM+DIS+PIRATIO+B+LSTAT,data=df1)  # 使用变换后的y值建立回归方程
summary(lm_bc)

c.加权最小二乘法（特殊的广义最小二乘）

其原理是：对残差估计值较小的变量赋予较大的权数，对残差估计值较大的赋予较小的权重。

参考文章：R语言作加权最小二乘_R语言与计量经济学（三）异方差_weixin_39672443的博客-CSDN博客

· lm(y~x,weight=)

#加权最小二乘法
e<-summary(fit3)$resid
lm_weight<-lm(MEDV~ZN+CHAS+NOX+RM+DIS+PIRATIO+B+LSTAT+I(RM^2)+I(1/LSTAT),
                df1,weight=1/abs(e))
summary(lm_weight)
ncvTest(lm_weight)

3.2综合验证

>gvlma()

library(gvlma)
gvmodel<-gvlma(fit)
summary(gvmodel)

六、实证部分

#一、基础准备

library(car)
library(MASS)
library(pastecs)#描述性统计

des_stat<-stat.desc(df)
#输出为csv文件
write.table(des_stat,"F:/个人嘿嘿嘿/北师大BNU/研一上-课业资料/应用多元线性回归/hw02多元回归/描述性统计.csv",sep=",")

#一、数据准备
df<-read.csv('F:/个人嘿嘿嘿/北师大BNU/研一上-课业资料/应用多元线性回归/hw02多元回归/boston_housing_data.csv')
df<-df[2:506,1:14] #剔除标题行
dim(df)

#前13列是自变量，第14列是响应变量
#给行和列命名
colnames(df)<-c("CRIM","ZN","INDUS","CHAS","NOX","RM","AGE",

                "DIS","RAD","TAX","PIRATIO","B","LSTAT","MEDV")
rownames(df)<-seq(1:505)

#二、基本OLS

fit<-lm(MEDV~ CRIM+ZN+INDUS+CHAS+NOX+RM+AGE+DIS+RAD+TAX+PIRATIO+B+LSTAT,data=df)
summary(fit)

#三、模型初步检查

多重共线性

#3.1诊断多重共线性
vif_judge<-function(fit_test){
  print(vif(fit_test))
  sqrt(vif(fit_test))>2
}
vif_judge(fit1)

#岭回归
library(MASS)
gr<-lm.ridge(MEDV~ CRIM+ZN+INDUS+CHAS+NOX+RM+AGE+DIS+RAD+TAX+PIRATIO+B+LSTAT,

             data=df1,

             lambda=seq(0,100,0.01))

#绘制岭迹图
plot(gr,data =df1,lambda = seq(0,100,0.01))
matplot(gr$lambda,t(gr$coef),type='l',

        xlab=expression(lambda),

        ylab=expression(hat(beta)),

        main ='Ridge trace Map')

#选择出合适的lambda
select(gr)

变量选择：AIC逐步回归法，全自集回归 

#3.2变量选择

#逐步回归法stepwise method
#删除了CRIM和INDUS
stepAIC(fit1,direction="backward")

#全子集回归
#显示：删除CRIM INDUS AGE RAD TAX
library(leaps)
leaps<-regsubsets(MEDV~ CRIM+ZN+INDUS+CHAS+NOX+RM+AGE+DIS+RAD+TAX+PIRATIO+B+LSTAT,

                  data=df1,nbest=14)
plot(leaps,scale="adjr2")

#模型二：变量选择后OLS
fit2<-lm(MEDV~ZN+CHAS+NOX+RM+DIS+PIRATIO+B+LSTAT,

         data=df1)
summary(fit2)

#3.3异常点判断
influencePlot(fit,id.method="identify",main="Influence Plot",sub="Circle size is proportional to Cook's distance")

#3.3.1高杠杆值点
#365 380 405 410 418
hat.plot <- function(fit) {
  p <- length(coefficients(fit))
  n <- length(fitted(fit))
  #hatvalues(fit)是计算fit中每个因变量的帽子统计量
  plot(hatvalues(fit),main = "Index Plot of Hat Values")
  abline(h=c(2,3)*p/n,col="red",lty=2)
  identify(1:n,hatvalues(fit),names(hatvalues(fit)))
}
hat.plot(fit)

#3.3.2强影响点
#368 371 372 380 418
cutoff <- 4/(nrow(df)-length(fit$coefficients)-2)
plot(fit, which = 4, cook.levels = cutoff)
abline(h=cutoff,lty=2,col="red")

#剔除异常值
df1<-df[-c(364,365,368,371,372,380,405,410,418),]
dim(df1)
fit1<-lm(MEDV~ CRIM+ZN+INDUS+CHAS+NOX+RM+AGE+DIS+RAD+TAX+PIRATIO+B+LSTAT,
        data=df1)

#四、回归诊断

#四、回归诊断
#粗糙的回归诊断
par(mfrow=c(2,2))
plot(fit2)

#4.1进一步：正态性检验
qqPlot(fit2,labels=row.names(df),id.method="identify",simulate=TRUE,main='Q-Q Plot')

#4.2进一步：独立性检验
durbinWatsonTest(fit2)

#4.3进一步：线性检验
crPlots(fit2)

#针对线性的修正：
fit3<-lm(MEDV~ZN+CHAS+NOX+RM+DIS+PIRATIO+B+LSTAT+I(RM^2)+I(1/LSTAT),data=df1)
summary(fit3)
durbinWatsonTest(fit3)

#4.4进一步：同方差检验
ncvTest(fit2)
#计分检验显著（p=0.32607),说明不拒绝同方差原假设
spreadLevelPlot(fit)

#4.4.1解决方案：加权最小二乘法->异方差
e<-summary(fit3)$resid
lm_weight<-        
    lm(MEDV~ZN+CHAS+NOX+RM+DIS+PIRATIO+B+LSTAT+I(RM^2)+I(1/LSTAT),df1,weight=1/abs(e))
summary(lm_weight)
ncvTest(lm_weight)

box-cox变换

#4.5box-cox变换

library(MASS)
bc<-boxcox(MEDV~ZN+CHAS+NOX+RM+DIS+PIRATIO+B+LSTAT,data=df1,lambda=seq(-2,2,0.01))

# λ的取值为区间[-2,2]上步长为0.01的值，bc中保存了λ的值及其对应的对数似然函数值
lambda<-bc$x[which.max(bc$y)]  # 将使对数似然函数值达到最大的λ复制给lambda
lambda

y_bc<-(df1$MEDV^lambda-1)/lambda  # 计算变换后的y值
lm_bc<-lm(y_bc~ZN+CHAS+NOX+RM+DIS+PIRATIO+B+LSTAT,data=df1)  # 使用变换后的y值建立回归方程
summary(lm_bc)

#再次诊断
durbinWatsonTest(lm_bc)
ncvTest(lm_bc)

GLS法

#4.6GLS
fit_gls<-lm(MEDV~ZN+CHAS+NOX+RM+DIS+PIRATIO+B+LSTAT,
            data=df1)
summary(fit_gls)

durbinWatsonTest(fit_gls) #DW=1.0827 p=0 不互独
ncvTest(fit_gls) #p=0.00011125 异方差