【论文阅读】Paraformer工业级非自回归端到端语音识别模型

论文下载

摘要

目前ASR常用的Transformer模型虽然效果比较好，但是因为引入了自回归的解码器，所以计算相对低效率。为了加速推理，设计了非自回归模型并行生成识别结果，比如单步自回归模型。然而由于输出标签之间的独立性假设，单步会自回归模型的效果相比自回归模型会差一些。对于提升单步非自回归模型来讲一共有两个挑战：第一个挑战是准确地预测输出标签的个数并提取隐变量；第二个挑战是增强输出标签间的非独立性建模。 为了解决上述两个挑战，作者提出了一个快速准确的并行transformer模型，标记为Paraformer。该模型属于单步非自回归模型。

1. Paraformer使用基于CIF的predictor预测输出标签的个数并产生隐变量；（借鉴文献【18】）
2. GLM sampler用于产生语义向量增强非自回归模型对上下文的建模能力；（借鉴文献【19】）
3. 最后作者设计了一个策略产生负例，并用MWER损失训练使模型的识别能力进一步提升。（借鉴文献【20】）

在公开的AISHELL1和AISHELL2和工业级2w小时任务上的实验结果显示，Paraformer可以获得和当前最优自回归模型相当的识别效果，但是可以提速10倍+。

介绍

端到端语音识别效果已经超过了传统的层级系统。主要有三种流行的E2E架构：CTC、RNN-T、AED。其中AED在序列到序列建模中具有统治性地位，因为其识别准确率高，比如transformers和conformers。虽然语音识别效果好，但是自回归模型比如AED模型需要一个一个地生成识别标签。因此，解码器的计算比较低效，随着输出序列的长度增加解码耗时线性增加。为了提升效率加速推理，许多研究【文献6～8】提出了非自回归模型并行输出识别结果。

基于推理时需要的迭代次数，非自回归模型可以分为单步式非自回归模型和迭代式非自回归模型。A-FMLM【文献9】是单步自回归模型的最早尝试，根据未被遮蔽的标签去预测遮蔽的标签。识别性能受到需要预测目标序列的长度的影响。为了解决这个问题，MASK-CTC和变种提出使用CTC的解码结果增强解码的输入【文献10-12】。最近，出现了单步非自回归模型用来解决上述的限制【文献13-17】。这些模型通过去掉时间依赖同时生成输出序列。 虽然单步非自回归模型可以显著提升推理速度，但是他们的识别性能相比自回归模型差一些，尤其是在大规模数据集上。

前面提到的单步非自回归模型主要关注如何预测输出标签的个数和准确提取隐变量。和机器翻译通过predictor预测输出标签个数相比，ASR预测输出标签个数确实比较难，因为有很多的潜在影响因素比如说话人的语速、静音、噪音等。另一方面，经过作者的观察和分析，单步非自回归模型相比自回归模型具有更多的替换错误，如下图1。作者认为缺少上下文依赖信息导致预测标签个数准确率差不多，替换错误上升明显(AR和vanilla NAR比较)，尤其是单步自回归模型条件独立假设。另外，所有的非自回归模型都是在学术基准阅读音频上实验的，并没有验证这些模型在工业基准数据上的效果。这篇论文的目标是提升单步非自回归模型的识别效果，使其达到和自回归模型相同水的水准，并在大规模数据上验证。
图片

文章提出了一个又快又准的并行transformer模型，可以克服上面提到的两个挑战。首先，不像前面的基于CTC的工作，作者提出了使用基于CIF的predictor网络评估目标长度并产生隐变量。对于第二个挑战，作者设计了基于GLM的sampler模块增强非自回归解码器的对输出变迁上下文建模能力。这个工作受到了机器翻译工作的启发。作者另外设计了一个包含负例的策略，利用MWER损失进行学习提升模型性能。

实验结果

AISHELL1 178h 5.2%

AISHELL2 1000h 6.19%

超过其它的非自回归模型方法，接近自回归模型效果。没有使用语音模型/无监督预训练。
Paraformer是第一个在性能上可以和自回归模型媲美，并且在大规模数据集上相比自回归模型有10倍+的推理速度提升。

方法

整体框架

如上图所示，整个框架包含五个模块：encoder、 predictor、sampler、decoder、loss function。其中Encoder和自回归模型的Encoder一样，本文使用是SAN-M和FFN(【文献21】)，也可以使用conformer等结构。Predictor用于生成声学特征指导解码。Sampler模块使用声学特征和标签特征生成语义特征。Decoder和自回归解码器相同，只不过这里是双向解码器。解码器包含多个SAN-M、FNN和cross MHA模块。除了CE loss，还会使用MAE loss训练predictor，MWER损失也一起用与模型训练。
整个流程阐述：
输入音频为X，长度为T；音频对应的文本标签为Y，长度为N。Encoder的输入为X，输出为H。Predictor的输入为H，输出为预测的输出标签长度N’并生成声学向量E_a。第一轮解码Decoder的输入为H和E_a，输出为Y’。图中红色虚线Pass1标记部分表示输入E_a，但是并不对这个输入进行反向传播学习。第二轮解码前会首先经过Sampler模块。Sampler模块在声学向量E_a和输出标签向量E_c之间进行采样得到语义向量E_s。其中Char指的是标签Y。采样过程依赖Y和Y’之间的距离。第二轮解码Decoder的输入为H和E_s，输出为Y’‘，这次进行反向传播学习。此次反向传播学习指导decoder学习上下文语音信息，同时也会指导predictor和encoder的学习。Sampler使用Y’进行距离计算不会进行反向传播学习。最后输出的Y’'会被采样为MWER训练生成负例候选。使用N和N’计算MAE。MWER和MAE和CE loss一起作为loss进行训练。
**推理时，sampler模块是不激活的，并且双向并行解码器只使用声学向量E_a和隐向量H输出通过一轮输出最终的预测结果。**尽管decoder在每次训练时会前向推理两次，但是因为在推理时只进行了一次所以并不会使计算复杂度变大。

Predictor

Predictor由两个卷基层组成，输出的float weight $\alpha$在0～1之间。作者通过累计此权重预测输出标签的长度。MAEloss定义为：

其实就是将所有$\alpha$进行了累加，加起来的长度就是预测的长度。LOSS就是真实长度和预测长度差的绝对值。作者引入了CIF机制产生声学向量。CIF是一个软的(非0/1，可以是小数)和单一的对齐，在AED模型中作为流式解决方案的实现【文献18】。声学向量的生成时，CIF对权重$\alpha$进行累计，如果超过了设定的阈值$\beta$，说明某一个声学向量的边界确定了。对边界之内的向量H根据权重$\alpha$进行缩放累计即可得到某一个声学向量。此过程重复直到结尾，可得到所有的声学向量。如下图所示：

在训练时权重$\alpha$会根据N进行缩放(比如累计的$\alpha$为N’，使用N/N’对所有的$\alpha$进行缩放，使用缩放后的$\alpha$计算声学向量E_a。缩放是为了让的E_a维度和E_c的维度保持一致)，但是在推理时无法进行缩放，导致训练和推理之间存在不一致。为了弥补这个不一致，作者提出了使用动态阈值$\beta$而不是固定阈值。计算公式如下：

下面是一个向上取整，所以分子小于等于分母，阈值$\beta <=1$。

Sampler

在普通的单步非自回归模型中，优化的目标为：$${\mathcal{L}}_{NAT}=\sum _{n=1}^{N}logP(y_n|X;\theta )$$然而，正如上面所说的，单步非自回归模型中的输出标签独立性假设导致模型识别效果不如自回归模型。同时，GLM模块的loss定义如下：
$${\mathcal{L}}_{GLM}=\sum _{y^{\prime \prime }\in \overline{\mathbb{GLM}(Y,Y^{\prime })}}logp[y_n^{\prime \prime }|\mathbb{GLM}(Y,Y^{\prime }),X;\theta ]$$

其中$\mathbb{GLM}(Y,Y^{\prime })$表示Sampler模块在$E_a$和$E_c$中选中$E_c$替换$E_a$对应的token的集合；$\overline{\mathbb{GLM}}(Y,Y^{\prime })$表示Sampler模块在$E_a$和$E_c$中未选中$E_c$替换$E_a$对应的token的集合；$\mathbb{GLM}(Y,Y^{\prime })$的定义如下：
$$\mathbb{GLM}(Y,Y^{\prime })=Sampler(E_s|E_a,E_c,\lceil \alpha d(Y,Y^{\prime })\rceil )$$ 上面公式的含义是从$E_c$中采样$\lceil \alpha d(Y,Y^{\prime })\rceil$个向量替换对应位置的$E_a$，生成新的向量为$E_s$。其中$\alpha$是控制采样率的采样因子，越大表示使用$E_c$替换$E_a$的概率越大。该采样概率应该在最初模型效果不好时设置的稍微大一些，然后随着整个的训练过程的进行逐渐减小。为了达到增额目的，作者简单实用汉明距离，其定义为：
$$d(Y,Y^{\prime })=\sum _{n=1}^N(y_n\ne y_n^{\prime })$$
也就是，最开始的时候模型学习不好，$d$会比较大，当模型学习越来越好时，$d$也逐渐减小。表示最开始训练时，使用较多的$E_c$替换$E_a$，也就是上下文信息更多和准确，减小模型的学习难度；当模型学习的越来越好时，使用较少的标签信息迫使模型进一步学习。
总结，sampler模块结合了标注标签向量$E_c$，实现方法是随机替换$E_a$中$\lceil \alpha d(Y,Y^{\prime })\rceil$个向量生成新的含有语义的向量$E_s$。训练并行decoder使用语义上下文$\mathbb{GLM}(Y,Y^{\prime })$预测目标标签$\overline{\mathbb{GLM}}(Y,Y^{\prime })$，使模型学习输出标签之间的依赖关系。

Loss Function

一共定义了三个loss：CE、MAE、MWER。训练时进行联合训练：
$${\mathcal{L}}_{total}=\gamma {\mathcal{L}}_{CE}+{\mathcal{L}}_{MAT}+{\mathcal{L}}_{werr}^N(x,y^{\ast })$$
对于MWER，具体的计算公式如下：
$${\mathcal{L}}_{werr}^N(x,y^{\ast })=\sum _{y_i\in Sample(x,N)}\hat{P}(y_i|x)[\mathcal{W}(y_i,y^{\ast })-\hat{W}]$$
非自回归模型使用贪婪搜索，所以只有一个输出路径。正如前面提到的，在使用MWER训练时作者使用负例采样策略通过随机遮蔽top1分值标签产生多个候选路径。

实验

实验设置

在AISHELL1、AISHELL2以及工业级2wh数据集上验证上述方法的效果。其中工业级的测试集有两个：普通30h、远场15h。具体的工业级语料介绍可以参考文献21和28。RTF的测试在NVIDIA tesla V100上完成。

AISHELL-1 & AISHELL-2 数据集

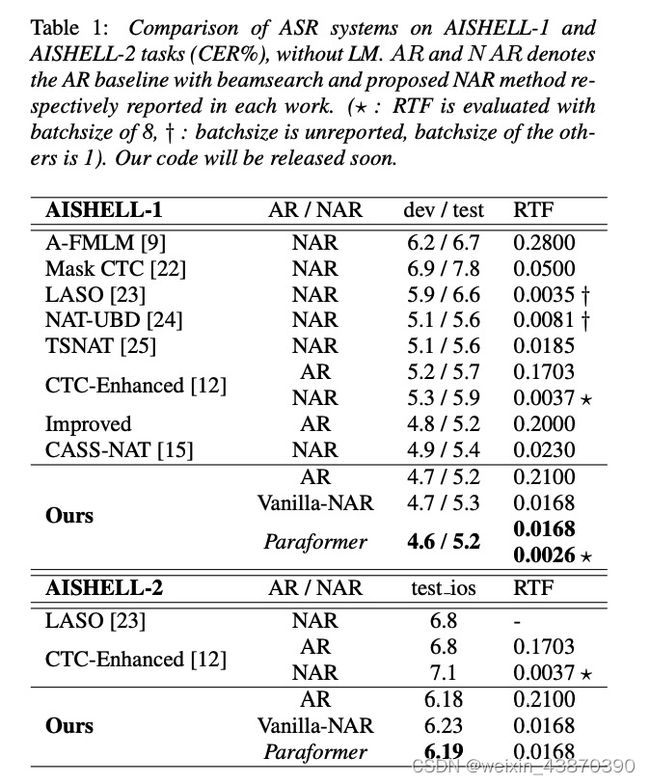
结果如上表格。在上述两个测试集上的测试都是在ESPNET框架上实现的，不包含LM和预训练模型。
AISHELL-1 的AR baseline参考文献15，效果在AR模型中是最好的，排除使用更多数据知识的模型。因为作者当前的目标是通过模型结构提升模型效果而不是通过数据。普通的NAR和Paraformer的结构相同，但是没有Sampler。

结论：
1. 普通NAR的表现超过了其它的NAR工作，比如文献15和文献12
2. 普通NAR模型的表现比AR模型稍微差一些，因为缺乏了输出标签之间的上下文信息。
3. Paraformer通过使用基于GLM的Sampler模块对普通NAR模型增强，得到了和AR模型相近的识别表现。
4. Paraformer模型在dev和test测试上的CER分别为：4.6%和5.2%，推理速度比AR基线模型快12倍。

AISHELL-2上的结论和AISHELL-1差不多。Paraformer在test_ios测试集上CER为6.19%，推理速度快12倍；

就目前所知，这是NAR模型在AISHELL-1和AISHELL-2上取得的最好识别结果。

工业级2wh数据集

结果如上表格所示，进行了多个扩展实验。动态$\beta$表示2.2节中的动态阈值，CTC表示带有LM的DFSMN-CTC-sMBR系统，参考文献32。RTF在OpenNMT上进行评估。
实验有两个模型，一个41M的一个63M的。AR基线模型中attention的维度为256，和文献21一致。这里的结论和前面有所不同。

结论

1. 可以看到在大型数据集上，普通NAR模型和AR模型的识别效果差距很大**(AISHELL上差别较小)。
2. 普通NAR模型虽然和CTC都有输出标签独立假设限制，但是普通NAR模型效果优于CTC效果。
3. 普通NAR模型结合GLM时，效果提升。
4. 当进一步结合MWER训练方法时，效果进一步提升。
5. Paraformer模型效果和AR模型效果很接近，差别在相对2%以内，但是推理速度提升10倍+。
6. Paraformer结合动态$\beta$，效果进一步提升。因为相比固定阈值，动态阈值减少了推理和训练的不一致，更准确地提取了声学向量信息。
7. 将模型变大时，得到了和前面相似的结论。Paraformer相比普通NAR模型效果提升；和AR模型效果相当，但是推理速度提升10倍+。
8. Paraformer-63M和AR transformer-41M模型相比较，尽管Paraformer模型较大，但是Paraformer推理速度更快。也就是说，在远场测试集上Paraformer-63M模型相比AR transformer-41M模型，识别效果相对提升6.0%，但是推理速度提升7.4倍。 也就是，在实际生产中，可以通过使用较大的Paraformer模型达到比AR模型更好的识别效果以及更快的推理速度。

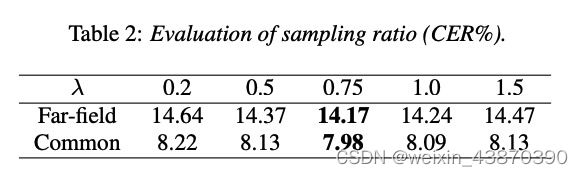
对采样因子$\alpha$的超参数测试结果参见上表格。和预期相同$\alpha$变大时，模型效果变好，因为在训练时提供了更多的上下文信息；然而如果该参数太大会导致训练和测试不一致。基本上，$\alpha$在0.5～1.0之间的表现比较稳定。

讨论

1. 在小型训练集上普通NAR和AR模型的识别性能差别不大，但是在工业级大数据集上差距明显。这是第一个在大规模工业级数据上验证NAR模型的效果。
2. Paraformer相比普通NAR模型识别效果相对提升11%，和精细训练的AR模型效果相当。

分析：见文章第一张图。

普通NAR模型相比AR模型，插入错误多一点，但是删除错误少一点。说明普通NAR模型的predictor预测输出的标签个数较准确。然而替换错误比较多，说明两者性能差距很大。作者认为是由普通NAR模型的条件独立假设造成的。Paraformer模型相比普通NAR模型替换错误下降很多，也暗示了识别效果提升很多。作者认为这是由于GLM模块使NAR模型学习到了标签之间的依赖关系。Paraformer模型相比AR模型替换错误稍微多一些，也暗示着识别准确率稍微差一些。作者认为AR的基于LM的beam search解码扮演了很重要的角色，相比GLM效果更好。为了减少这个性能差距，作者将在未来工作中在Paraformer模型上结合外部语言模型。

结论

1. 文章提出了一个单步NAR模型Paraformer。
2. Paraformer使用基于CIF的predictor预测输出标签的个数并产生隐变量；（借鉴文献【18】）
3. 改进CIF使用动态$\beta$阈值。
4. GLM sampler用于产生语义向量增强非自回归模型对上下文的建模能力；（借鉴文献【19】）
5. 最后作者设计了一个策略产生负例，并用MWER损失训练使模型的识别能力进一步提升。（借鉴文献【20】）
6. 在AISHELL-1 & AISHELL-2 数据集和大规模工业级数据上都验证了Paraformer效果和当前最优的AR模型效果相当，但是推理速度提升超过10倍。

个人思考/疑问

1. MWER loss没看懂，需要看文献20.
2. Char 的 Embedding使用的torch.nn.Embedding，直接学习嘛？还是预设值好的。
3. 端到端语音识别中的Embedding，例如wenet框架的token 的 Embedding能不能使用NLP领域用文字训练得到的Embedding，如果能的话为啥主流的不是这种的，这个Embedding不比直接学习更好嘛？
4. wenet的重打分架构，decoder能不能直接根据CTC N-best结果的到矫正的识别结果，相当于做矫正？
5. Paraformer能不能直接结合在当前的wenet框架中，使用conformer那套encoder，而不是SAN-M。从文章结论看，可以使用更大的模型训练Paraformer，效果比之前的模型效果好，且推理速度快，是一个可以实践的方向。
6. Paraformer结构能不能和wenet重打分那套结合？Pafaformer的输出替代CTC的那一支，然后再加上decoder部分的重打分。这样相当于有了两个decoder。按道理就是训练会慢，但是推理应该还好吧？可能可行。
7. 作者提出的在外面再结合一个语言模型可是可以的，这个比6训练代价小，但是速度不知道两种方案哪个会好些。