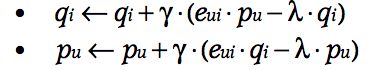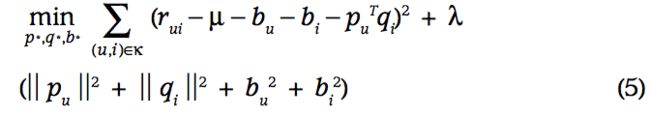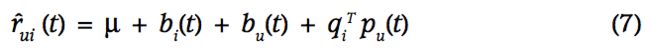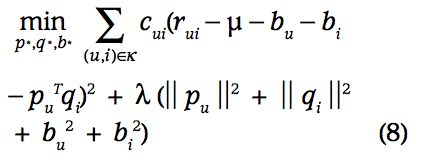【矩阵分解七】论文阅读MATRIX FACTORIZATION TECHNIQUES FOR RECOMMENDER SYSTEMS

总结：该论文将构造rating矩阵的多中种方式都讲述了一遍。主要讲ALS在优化参数时，优于SGD的方面，体现在对预测rui的组成部分的逼近。

---

introduction引言

推荐系统的基于两个策略content filtering ，比如，商品本身的属性，另一个是用户属性。基于内容的推荐策略，要求聚集一些额外的信息，这一班不太容易收集。

内容过滤策略的一个可替代方式是依赖于用户过往行为。称之为协同过滤，对冷启动问题，效果不好，因为协同过滤不能应对一个新物品或者新用户。(新商品或者用户而言，没有历史行为，因此不能将其归类。)

协同过滤领域有两个基础的方法，一个是近邻方法(基于item的方法)，一个是潜在因子模型。

近邻方法聚焦于计算item之间或者user之间的关系。商品之间的关系计算，通过用户过往历史行为过的item，计算items跟用户没有过行为的item之间的相似度，来得出用户对这个新item的喜好。

基于隐因子的方法，将item和user表示为20~100维度的因子，来解释评分。也就是矩阵分解后得到的k维度的向量，每一维，称之为一个隐因子，从某一个属性上来解释。对于user来说，每一个因子衡量了如何对用户喜欢的电影根据包含有相应的item因子计算得到高分。

矩阵分解因子方法

主要将隐因子方法，其中较为成功的获取隐因子的方式是矩阵分解。user和item之间的相关性，使得矩阵分解大放异彩，同时，矩阵分解使得模型对多变的真实情况有更好的适应性。

对于输入的数据，有explicit feedback ，显式反馈，显式表名用户对商品的喜爱程度。比如，netflix收集了电影的评分，我们称这种反馈形式为显式反馈。通常，显式反馈是一个稀疏矩阵，因为单个用户喜欢的商品是有限的，且相对于全部商品而言，是非常少量的。

对于矩阵分解来说，一个强大的点在于允许添加信息来填充矩阵。当显式反馈不适用的时候，我们引入隐式反馈implicit feedback，其中的元素由用户的浏览、点击、收藏行为组成。隐式反馈的一个优点在于补充了缺失的元素，更容易得到一个稠密的矩阵。

基础的矩阵分解模型

矩阵分解模型将user和item映射到一个f维的空间中，他们因子的内积表明了二者的相关程度。item i使用qi表示，user u用pu表示，这两个向量是其隐因子，可正可负。两者的内积q_iT* p_u,表示i和u之间的相似度。

主要的挑战是计算每一个商品和user的因子向量。上面的模型，联系到SVD，一个求解隐因子的方法。对于高缺失值和稀疏的矩阵来说，传统的svd求解，有点困难。并且，的到的结果也比较容易过拟合。

为解决缺失值问题，一种方法可是填充缺失值，但是人工填充，会增加计算代价，文献中提供了不精确的数据填充方式，加入正则化来避免过拟合。模型如下：

关于正则化的lambda，特别的提了一嘴，Ruslan Salakhutdinov and Andriy Mnih提出了 “Probabilistic Matrix Factorization ，PMF这种概率的方式建模来添加正则化。

学习算法

公式(2)使用两种方法来求解，一个是SGD(tochastic gradient descent )，一个是ALS(sand alternating least squares). 

SGD 

主要根据Funk-svd的优化方法，计算预测rui跟样本rui的差：

梯度更新：

ALS

因为p和q都未知，因此可以固定一个，可以使用最小二乘法去求解另外一个，直到方程2收敛。

SGD比ALS容易实现，更快的求解，但是ALS比SGD的优势：1，可以并行计算qi，因为qi的计算跟其他商品的qi独立，每一个qi都可以并行计算。2，对于聚焦于隐数据(这里意思，我理解是rating中的元素构成，不仅仅是q_iT* p_u,还有一些隐藏的信息，尚未添加到q_iT* p_u中，通过后面的介绍也可以看到，预测rui的构成更加多样化，考虑的因素也更多)有优势，因为训练数据不能是稀疏的，遍历全部训练样本(就像SGD一样)，是不现实，ALS能解决上述两种情况。

添加biases

添加bias指的是往预测值中添加bias。方程1中，尽力获取user和item的交互，产生不同的rating值，但是在在观测数据中，有值的元素依赖于用户或者item，独立于任何交互行为，换句话说，rating中的元素rui的组成，不仅仅是交互行为产生的，更加依赖于商品或者user本身。比如，有的人习惯性给高分，有的人则习惯性给低分，比较挑剔，这的rui就会收到user的影响；再比如，商品很好，人自然而然的给高分，如果商品很差劲，想给高分也难。

因此将rating矩阵中的rui解释为q_iT* p_u的乘积是不充分的。通过添加user和item的属性部分去解释交互数据之外的因子模型。bias的一阶近似如下：

Rui的bias由bui决定，包含了user和item的对rating的影响。U是rating的平均值，bu和bi是user和item的观察偏差。举个例子，rating的平均值U=3.7，item泰坦尼克号是一个非常好的电影，高于平均分0.5，而user jon是一个非常挑剔的人，给出的打分通常低于平均费0.3，综合得分为3.7+0.5-0.3=3.9；

预测值由4部分构成：rating矩阵、item的bias、user的bias、user-item的交互。

损失函数是：

通过观测数据捕捉bias，对精确建模比较重要，因此后续也在此工作上做了一些内容。

添加输入源-加入隐式反馈

很多系统必须处理冷启动问题，很多用户有很少的评分行为，很难对他们的喜好得到一个一般化的结论。一个解决的办法就是给user添加信息源。推荐系统使用隐式反馈来观察user的喜好，通过汇集用户的行为信息去显示的rating。比如一个零售商会根据用户买过的东西来推测他们喜欢什么。

简而言之，用一个boolean值表示隐式反馈。

N(u) ：用户u有过隐式反馈行为的item集合；

用户对N(u)中的商品表示为：

添加正则化：

另一个信息源来自用户的属性，比如统计属性。A(u)表示用户的统计信息集合，比如性别，年龄，收入水平等。用隐因子ya描述用户：

矩阵分解模型中聚合各种信息后，预测结果表示为：

这个例子增强了用户的表示，显然缺少item的信息，接下来继续看。

动态模型

目前为止展示的模型都是静态的，在实际生活中，商品的热度是变化的，用户的偏好也在变化。user-item之间的交互是收时间影响的。

那么矩阵分解方法也趋向于添加时间因素去建模，更加精准。主要的变动，在item的bias - bi(t)和user的bias-bu(t)，以及user的偏好pu(t).为什么没有q(t)呢？item相对变换更缓慢一些，可以认为是静态的，不会在短时间内发生变化。

对输入置信水平

不是所有观测到的rating都有相同的权重或者置信度。比如大量的广告，会影响某些item的rui。

置信度可以是一些数值描述行为的频率，比如，展示或者购买的次数。这个置信度想说明，偶然一次的行为，可能对这些隐因子没有贡献，而循环多次的行为表明了用户的观点喜好，对隐因子有贡献。

Cui是观测值rui的置信度：

Netflix大赛，以0.843勇夺number1.也不知道最近两年有没有人打这个比赛，超越这个论文中的第一名。

参考：

1.论文：MATRIX FACTORIZATION TECHNIQUES FOR RECOMMENDER SYSTEMS