R语言-假设检验
目录
- 假设检验
-
-
- 假设检验的原理
- 1. 提出假设
- 2. 做出决策
- 3. 表述结果
- 4. 效应量
-
- 1.总体均值的检验
-
- 1.1 一个总体均值的检验
-
- 1.1.1大样本的检验
- 1.1.2 小样本的检验
- 1.2 两个总体均值只差的检验
-
- 1.2.1 独立大样本的检验
- 1.2.2 独立小样本的检验
- 1.2.3 配对样本的检验
- 1.3 总体比例的检验
-
- 1.3.1 一个总体比例的检验
- 1.3.2 两个总体比例只差的检验
- 1.4 总体方差的检验
-
- 1.4.1 一个总体方差的检验
- 1.4.2 两个总体方差比的检验
- 数据下载
假设检验
假设检验的原理
- 假设检验的答题思路:
- 首先,对所关心的总体提出某种假设
- 然后,从待检验的总体中抽取一个样本并获得数据
- 再根据,样本提供的信息判断假设是否成立
- 参数检验 – 如果已知总体分布或能对总体分布做出假定,而所关注的仅仅是总体的某个参数,并对参数的某个假设做检验,成为参数检验
- 非参数检验 – 如果是对总体的其他特征(如分布的形式)做检验,或者是样本数据不满足参数检验条件,不依赖于总体分布的形式对总体参数做检验,成为 非参数检验
1. 提出假设
- 原假设 H0 :是研究者想收集证据予以推翻的假设,‘=’总是放在原假设上,
- 原假设总是写成:H0:μ = μ0;H0:μ ≥ μ0;H0:μ ≤ μ0
- 原假设最初被假设是成立的,之后根据样本数据确定是否有足够的证据拒绝原假设。
- 备择假设 H1:通常是研究者想收集证据予以支持的假设
- 备择假设的形式总是: H1:μ ≠ μ0 ; H1:μ < μ0 ;H1:μ > μ0
- 备择假设通常用于表达研究者自己倾向于支持的看法,然后就是想办法收集证据拒绝原假设,以支持备择假设
- 双侧检验 or 双尾检验 :备择假设没有特定的方向,并含有’≠‘ 这样的假设成为 【双侧检验】或【双尾检验】
- 单侧检验 or 单尾检验:备择假设还有符号“<” 的单侧检验成为【左侧检验】,而含有符号“>”的单侧检验成为【右侧检验】
2. 做出决策
-
两类错误于显著性水平:
- 第I类错误:又称α错误,原假设是正确的却拒绝了它
- 第II类错误:又称β错误,原假设是错误的却没有拒绝它
-
在假设检验中,只要做出拒绝原假设的决策,就有可能犯第I类错误;
-
只要做出不拒绝原假设的决策,就有可能犯第II类错误;
-
直观上说,这两类错误之间的关系为:在样本量不变的情形下,要减小α就会使β增大,而要减小β就会使α增大。
-
要使两类错误同时减小的唯一办法就是增加样本量,但样本量的增加又会受许多因素的限制
-
一般来说,发生哪一类错误的后果更严重,就应该先控制哪类错误发生的概率,由于犯第I类错误的概率可以由研究者事先控制,而犯第II类错误的概率则相对难以计算,
-
因此在假设检验中,人们往往先控制第I类错误发生的概率。
-
显著性水平:犯第I类错误的概率成为显著性水平,记为 α
-
常用的显著性水平有: α = 0.01 ,α = 0.05, α = 0.1
-
决策的依据:
- 传统检验中,决策依据的是样本统计量。(不推荐使用)
- 双侧检验:|统计量的值| > 临界值,拒绝原假设
- 左侧检验:统计量的值 < -临界值,拒绝原假设
- 右侧检验:统计量的值 > 临界值,拒绝原假设
- 现代检验中,人们直接更具样本数据算出犯第I类错误的概率,即P值(p-value)
- P值觉得规则很简单,如果 P < α 拒绝H0 ; 如果 P > α,不拒绝H0(双侧检验将两侧面积的总和定义为P)
3. 表述结果
-
当拒绝H0时称样本结果是“统计上显著的”;
-
不拒绝H0 则称结果是“统计上不显著的”
-
当P < α 拒绝H0时,表示有足够的证据证明H0时错误的;当不拒绝H0时,通常不说“接受H0”,因为“接受H0”的表述隐含着证明了H0时正确的。
-
实际上,P值只是推翻原假设的证据,而不是证明原假设的证据。
-
采取“不拒绝H0”而不是“接受H0”的表述方法也避免了第II类错误发生的风险,
4. 效应量
- 效应量(effect size) : 当假设检验拒绝原假设时,表示参数与假设值之间差异显著,但这一结果并未告诉我们差异的大小(程度),度量差异大小的统计量就是【效应量】,它描述了结果的差异程度是小、中、还是大。
1.总体均值的检验
1.1 一个总体均值的检验
1.1.1大样本的检验
- 例:为检测空气质量,某城市环保部门每隔几周对空气中的PM2.5进行一次随机测试,已知该城市过去每立方米空气中PM2.5的均值是81μg/m^3。在最近一段时间的40次检测中,每立方米空气的PM2.5数据如数据集所示。
- 问:根据最近的测量数据,能否认为该城市每立方米空气中PM2.5的均值显著低于81(α=0.05)
- 假设: H0: μ ≥ 81 , H1: μ < 81
data_1 = read.csv('***.csv')
library(lattice)
library(BSDA)
a = 0.05
z.test(data_1$PM2.5值,mu=81,sigma.x=sd(data_1$PM2.5值),alternative="less",conf.level=1-a)
- 结论:在该项检验中,x_bar = 79.55,z = -1.1856,P = 0.1179 ,由于 P > a(0.05),不拒绝H0,没有证据表明该城市空气中的PM2.5均值显著低于81
1.1.2 小样本的检验
- 例: 一种建筑用砖的厚度要求为5cm,高于或低于该标准均被认为是不合格的,现对一家生产企业提供的20快样本进行检测,结果如数据中所示。
- 问:假定砖的厚度服从正态分布,在0.05显著性水平下,检验该企业生产的砖的厚度是否符合要求。
- 假设: H0: μ = 5 ,H1: μ ≠ 5
data_2 = read.csv('***.csv')
t.test(data_2$厚度,mu=5)
- 结论: 在该项检验中,x_bar = 4.8,t = -5.6273 ,P = 1.998e-05,由于P<0.05,拒绝H0,有证据显示该企业生产的砖的厚度不符合要求。
library(lsr)
cohensD(data_2$厚度,mu=5)
#### 输出结果
1.258306
- 检验结果:表示样本砖的平均厚度与标准厚度相差1.258306个标准差,根据Cohen准则,该检测结果属于大的效应量。
1.2 两个总体均值只差的检验
1.2.1 独立大样本的检验
- 例:为分析男女学生上网时间是否有差异,从男女学生中各随机抽取36人,得到每天的上网时间数据,
- 问:在显著性水平0.05下,检验男女学生上网的平均时间是否有显著差异。
- 假设:μ1 = 男生上网的平均时间,μ2 = 女生上网的平均时间,由于关心上网的平均时间是否有显著差异,H0:μ1 - μ2 = 0;H1:μ1 - μ2 ≠ 0
data_3 = read.csv('***.csv')
library(BSDA)
z.test(data_3$男生上网时间,data_3$女生上网时间,sigma.x = sd(data_3$男生上网时间),sigma.y = sd(data_3$女生上网时间),alternative = "two.sided")
- 结论:在该项检验中,x_bar男=3.058333 ,x_bar女=2.830556 ,z=1.1188,P=0.2632,由于P>α(0.05),不拒绝H0,没有证据显示男女学生上网的平均时间有显著差异。
1.2.2 独立小样本的检验
- 例:为比较两家企业生产的灯泡平均使用使用寿命是否有显著差异,质检人员对两家供货商提供的各20个样本进行检测,得到的使用寿命数据如表所示。
- 问:检验两家企业灯泡的平均使用寿命是否有显著差异(α=0.05):1.假设两个总体方差相等。2.假设两个总体方差不相等。
- 假设:μ1为甲企业灯泡的平均使用寿命,μ2为乙企业灯泡的平均使用寿命,
- H0:μ1 - μ2 = 0 ,H1:μ1 - μ2 ≠ 0
data_4 = read.csv('***.csv')
# 总体方差相等
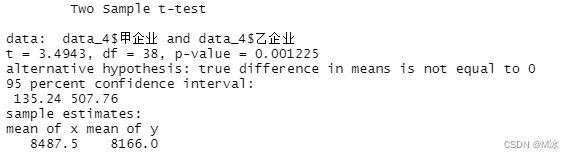
t.test(data_4$甲企业,data_4$乙企业,var.equal=TRUE)
# 总体方差不相等
t.test(data_4$甲企业,data_4$乙企业,var.equal=FALSE)
- 结论:在该项检验中,x_bar甲=8487.5 ,x_bar乙=8166.0 ,
- 假设总体方差相等时:t=3.4943,df=38,P=0.001225,
- 假设总体方差不相等时: t=3.4943,df=33.683,P=0.001353
- 两种假设条件下检验的P值都小于0.05,所以拒绝H0,表明两家企业生产的灯泡平均使用寿命有显著差异
- 效应量检验
library(lsr)
cohensD(data_4$甲企业,data_4$乙企业)
#### 输出结果
1.104985
- 检验结果:d=1.104985,表示甲企业和乙企业的灯泡平均使用寿命相差1.104985个标准差,根据Cohen准则,该检验结果属于大的效应量
1.2.3 配对样本的检验
- 例:某饮料公司研制除一款新产品,为比较消费者对新旧产品口感的满意程度,随机抽选一组消费者共10人,让每个消费者先品尝一款饮料,再品尝另一款饮料,两款饮料的品尝顺序时随机的,而后每个消费者要对两款饮料分别进行评分(0-10分),评分结果如数据所示。
- 问:取显著性水平α=0.05,检验消费者对两款饮料的评分是否有显著差异。
- 假设:μ1 = 消费者对旧款饮料的平均评分,μ2=消费者对新款饮料的平均评分
- H0:μ1 = μ2 = 0,H1:μ1 - μ2 ≠0
data_5 = read.csv('***.csv')
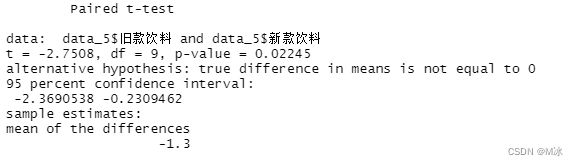
t.test(data_5$旧款饮料,data_5$新款饮料,paired=TRUE)
- 结论:在该项检验中,d_bar = -1.3 ,t=-2.7508,df=9,P=0.02245,由于P<0.05,拒绝H0,消费者对新旧饮料的评分有显著差异。
- 效应量检验
library(lsr)
cohensD(data_5$旧款饮料,data_5$新款饮料,method="paired")
- 检验结论: d=0.8698945,根据Cohen准则,该检验结果属于大的效应量
1.3 总体比例的检验
1.3.1 一个总体比例的检验
- 例: 一家电视台的影视频道制作人认为,某电视连续剧如果在黄金时段播出,收视率将会达到25%以上,经过一周的试播后,该制作人随机抽取了由2000人组成的一个样本,发现由450名观众观看了该电视剧。
- 问:取显著性水平 α=0.05,检验收视率是否达到制作人的预期。
- 假设:制作人想支持的观点是收视率达到25%以上,因此假设为:H0≤25%,H1>25%
n = 2000
p =450/2000
pi0 = 0.25
z = (p-pi0)/sqrt(pi0*(1-pi0)/n)
p_value = 1-pnorm(z)
data.frame(z,p_value)
### 输出结果
z p_value
1 -2.581989 0.9950884
- 结论: 该项检验中,z=-2.581989,P=0.9950884, 由于P>0.05,不拒绝H0,没有证据表明收视率达到了制作人的预期。
1.3.2 两个总体比例只差的检验
- 例1:一所大学准备采取一项新的上网收费措施,为了解男女生对这一措施的看法是否由差异,分别抽取200名男生和200名女生进行调查,其中的一个问题是:“你是否赞成采取新的上网收费的措施?”其中,男生表示赞成的比例为27%,女生表示赞成的比例为35%,调查认为,男生中表示赞成的比例显著低于女生。
- 问:取显著性水平α=0.05,样本提供的证据是否支持调查者的看法?
- 假设:pi1=男生中表示赞成的比例,pi2=女生中表示赞成的比例,提出假设:H0:pi1 - pi2 ≥ 0, H1:pi1-pi2 < 0
n1 = 200
n2 = 200
pi1 = 0.27
pi2 = 0.35
p = (pi1*n1+pi2*n2)/(n1+n2)
z = (pi1-pi2)/sqrt(p*(1-p)*(1/n1+1/n2))
p_value = pnorm(z)
data.frame(z,p_value)
##### 输出结果
z p_value
1 -1.729755 0.04183703
-
结论: 该项检验中,z=-1.729755,P= 0.04183703,P<0.05,拒绝H0,样本提供的证据支持调查者的看法,即男生中表示赞成的比例显著低于女生。
-
例2:由两种方法生产同一种产品,方法1的生产成本较高而次品率较低,方法2的生产成本较低而次品率较高,管理人员在选择生产方法时决定对两种方法的次品率进行比较。
-
如果方法1比方法2的次品率低8%以上,则采用方法1,否则就采用方法2,管理人员从采用方法1生产的产品中随机抽取300个,发现由33个次品;从采用方法2生产的产品中也
-
随机抽取300个,发现由84个次品。
-
问:用显著性水平α=0.01进行检验,管理人员应决定采用哪种方法进行生产。
-
假设:pi1=方法1的次品率,pi2=方法2的次品率,因为要检验方法1的次品率是否比方法2低8%,H0:pi1 - pi2 ≥ 8% ,H1: pi1 - pi2 < 8%
n1 = 300
n2 = 300
pi1 = 33/300
pi2 = 84/300
d0 = 0.08
z = ((pi1-pi2)-0.08)/sqrt(pi1*(1-pi1)/n1+pi2*(1-pi2)/n2)
p_value = pnorm(z)
data.frame(z,p_value)
##### 输出结果
z p_value
1 -7.91229 1.26348e-15
- 结论:该项检验中,z=-7.91229,P=1.26348e-15,P<0.01,拒绝H0,表示方法1的次品率显著低于方法2达8%以上,所以采用方法1进行生产
1.4 总体方差的检验
1.4.1 一个总体方差的检验
- 例:啤酒生产企业采用自动生产线灌装啤酒,每瓶的填装量为640mL,但由于某些不可控因素的影响,每瓶的填装量都会有差异,如果σ^2很大,会出现装填量太多或太少的情形,这样,要么生产企业不划算,要么消费者不满意。
- 假定生产标准规定每瓶填装量的方差不应超过16,企业质检部门抽取了10瓶啤酒进行检验,得到的样本数据如下,
- 问:检验方差是否符合要求(α=0.05)
- 假设:H0: σ^2 ≤ 16,H1:σ^2 > 16
data_6 = read.csv('***.csv')
library(TeachingDemos)
sigma.test(data_6$填装量,sigmasq = 16,alternative="greater",conf.level=0.95)
- 结论:该项检验中,s^2=5.287222 ,X-squared = 2.9741,df=9,P = 0.9653,由于P>0.05,不拒绝H0,没有证据显示啤酒填装的方差不符合要求。
1.4.2 两个总体方差比的检验
- 例:为比较两家企业生产的灯泡平均使用使用寿命是否有显著差异,质检人员对两家供货商提供的各20个样本进行检测,得到的使用寿命数据如表所示。
- 问:检验两家企业灯泡使用寿命的方差是否由显著差异(α=0.05)
- 假设:甲企业灯泡使用寿命的方差为var1,乙企业灯泡使用寿命的方差为var2,
- H0:var1/var2 = 1,H1: var1/var2 ≠ 1
data_7 = read.csv('***.csv')
var.test(data_7$甲企业,data_7$乙企业,alternative="two.sided")
- 结论: 该项检验中,var1/var2=0.4727311 ,F=0.47273,df1=19,df2=19,P=0.111,p>0.05,不拒绝H0,没有证据表明两家企业灯泡使用寿命的方差由显著差异。
数据下载
- 所使用数据下载:https://download.csdn.net/download/weixin_44678403/85267404