贝叶斯网专题1：信息论基础

---

贝叶斯网专题前言

贝叶斯网是一种将概率统计应用于复杂领域，进行不确定性推理和数据分析的工具，其在机器学习和人工智能领域具有重要的基础性地位。从技术层面讲，贝叶斯网可系统地描述随机变量之间关系，构造贝叶斯网的主要目的是进行概率推理。
理论上，进行概率推理只需要一个联合概率分布即可，但联合概率分布的复杂度与随机变量规模呈指数级关系，在解决实际问题时不可行。贝叶斯网为解决该问题提供了方法，通过贝叶斯网可将复杂的联合概率分布分解为一系列规模较小的子模块，从而降低训练和推理的复杂度。
本人将主要依据香港科大张连文教授的《贝叶斯网引论》，对其中重要内容进行精炼，并通过接下来的几篇博客对贝叶斯网展开专题介绍，分三大部分进行：

• 第一部分介绍贝叶斯网基础，包括信息论基础和贝叶斯网相关概念，并手工构造贝叶斯网。
• 第二部分介绍贝叶斯网推理，包括推理原理和相关算法。
• 第三部分介绍贝叶斯网训练，包括已知网络结构下的参数估计、未知网络结构下的结构分析和参数估计，以及隐结构分析。

第一部分：贝叶斯网基础

1.1 信息论基础

信息论是基于概率论的一门研究信息传输和处理的数学理论。它不仅是信息技术的基础，也在统计力学、机器学习等领域发挥重要作用。在构建贝叶斯网的过程中，可以用信息论来进行分析。

1.1.1 预备数学知识：Jensen不等式

Jesen不等式源于函数的凹凸性。在数学中，称一个函数为凹函数是指向上凹，凸函数是指向下凸，如下图所示。

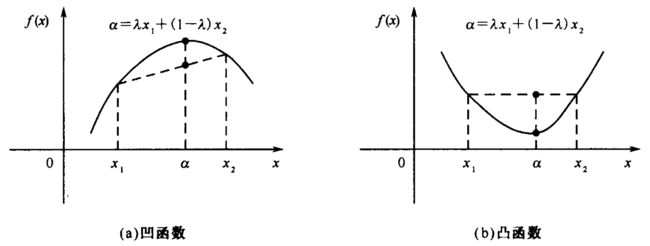
若一个函数$f$在实数轴的某个区间$I$上被称为凹函数，则有如下不等式成立：
$$\forall x_1,x_2\in I:f(\lambda x_1+(1-\lambda )x_2)\ge \lambda f(x_1)+(1-\lambda )f(x_2),\forall \lambda \in [0,1]$$
若式中等号只在$x_1=x_2$时成立，则称$f$在区间$I$上严格凹。若将式中不等号方向改变，则得到凸函数的定义。
我们看到，式中参数$\lambda ,1-\lambda$可以看做概率，由它们之和为1，不等号左侧可以看作输入的期望对应的输出，右侧可以看作输入对应的输出的期望。对于上凹函数，输入的期望对应的输出大于输入对应的输出的期望；对于下凸函数，则刚好相反。
Jensen不等式则是上式在期望意义上的推广。

Jensen不等式
设$f$为区间$I$上的凹函数，$p_i\in [0,1],i=1,2,\cdots ,n$，且${\sum }_{i=1}^n{p}_i=1$，则对任何$x_i\in I$，有：
$$f(\sum _{i=1}^n{p}_i{x}_i)\ge \sum _{i=1}^n{p}_{i}f(x_i)\text{\hspace{1em}(1)}$$
若$f$严格凹，则上式等号只在下列条件满足时才成立：若$p_i\cdot p_j\ne 0$，则必有$x_i=x_j$。

证明
用归纳法证明，当$n=1$时，式(1)恒等。假设式(1)在$n=k$时成立，证明它在$n=k+1$时也成立，即：
$$\begin{array}{rl}f(\sum _{i=1}^{k+1}{p}_i{x}_i)& =f(\sum _{i=1}^k{p}_i{x}_i+p_{k+1}{x}_{k+1})\\ & =f\left[(1-p_{k+1})\frac{1}{1-p_{k+1}}\sum _{i=1}^k{p}_i{x}_i+p_{k+1}{x}_{k+1}\right](假设p_{k+1}\ne 1)\\ & \ge (1-p_{k+1})f\left(\frac{1}{1-p_{k+1}}\sum _{i=1}^k{p}_i{x}_i\right)+p_{k+1}f(x_{k+1})(根据凹函数定义)\\ & =(1-p_{k+1})f\left(\sum _{i=1}^k\frac{p_i}{1-p_{k+1}}{x}_i\right)+p_{k+1}f(x_{k+1})\\ & \ge (1-p_{k+1})\sum _{i=1}^k\frac{p_i}{1-p_{k+1}}f(x_i)+p_{k+1}f(x_{k+1})(根据归纳假设)\\ & =\sum _{i=1}^k{p}_{i}f(x_i)+p_{k+1}f(x_k+1)\\ & =\sum _{i=1}^{k+1}{p}_{i}f(x_i)\end{array}$$
命题得证。
Jensen不等式是与函数凹凸性有关的基本性质，在信息论中常会用到，比如用于计算信息熵的对数函数就满足凹函数的Jensen不等式，这在后文证明信息熵的性质时会用到。

1.1.2 熵

一个离散随机变量$X$的熵$H(X)$的定义为：
$$H(X)=E_P[\log \frac{1}{P(X)}]=-\sum _{X}P(X)\log P(X)$$
其中，约定$0\log \frac{1}{0}=0$.上式的对数若以2为底，则熵的单位是比特，若以e为底，则单位是奈特，后文将都以比特为单位。
熵在热力学中表示系统的混乱程度，在概率论中表示随机变量的不确定程度，在信息论中表示对信源的期望编码长度。
先来解释下信息论中期望编码长度：假设有一个信源，可产生A、B、C三种不同的信息，产生的概率分别为1/2、1/4和1/4，我们要设计一套编码系统来记录这个信源所产生的信息，所用的比特位数越少越好。显然，我们应该为出现概率大的信息分配码长较短的编码，其长度可通过$\log \frac{1}{P(X)}$来确定，比如我们为A分配码长为1的编码，为B和C分配码长为2的编码，通过霍夫曼编码算法，可将A编码为0，将B和C编码为10和11.此时，该信源的编码平均码长则为$\frac{1}{2}\times 1+\frac{1}{4}\times 2+\frac{1}{4}\times 2=1.5$

霍夫曼编码算法：
Huffman使用自底向上构建二叉树的方式，构建编码树，每个字符的最终编码是从根走到叶子的01序列，往左走为0，往右走为1。
构建的方式也很简单：
a. 初始集合里有n棵树，分别表示待编码的n个字符，树根的值是这个字符出现的概率。
b. 选择树根值最小的两颗树，添加一个中间节点做根，两颗树作为左右子树，树根值是两颗子树的根值的和。删掉两颗子树，把新的中间节点做根的子树添加进集合。
c. 重复过程b，直到集合里只有一颗树。

由此我们可知，熵代表了对信源进行最优编码时的期望编码长度。反过来看，如果将这个信源用一个随机变量来表示，若该随机变量的不确定性越高（产生的信息种类越多、各种类出现的概率越平均），则需要用来编码该信源的期望编码长度也会越大，反之则越短。因而，熵又可以表示随机变量的不确定程度。
例如，一个取值为0或1的随机变量$X$，计$p=P(X=1)$，根据熵的定义，有：
$$H(X)=-p\log p-(1-p)\log (1-p)$$
随着p的变化，$H(X)$的变化曲线如下图：

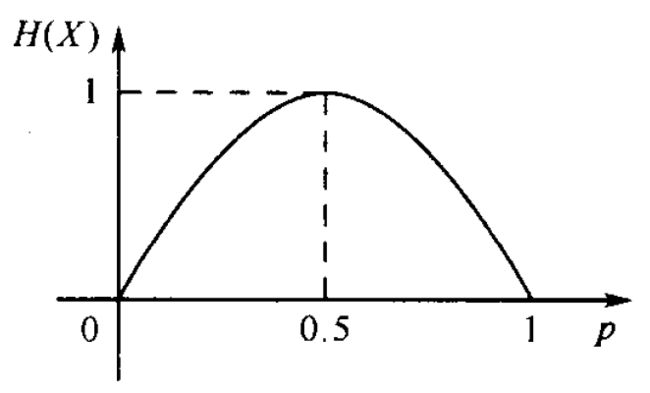
从上图可知，当p=0或者p=1时，随机变量X的取值是确定的，不确定性最小，H(X)=0.5时，X取值的不确定性最大，此时H(X)=1.
同样，我们可以用随机变量X、Y、Z分别表示掷硬币、掷骰子和从54张扑克牌中随机抽取一张的结果。显然X的不确定性最小，Z的不确定性最大。它们的熵则存在如下的关系：
$$\begin{array}{rl}& H(X)<H(Y)<H(Z)\\ & H(X)=1\\ & H(Y)=\log 6\\ & H(Z)=\log 54\end{array}$$
我们用$|X|$来计变量X的取值个数，又称为变量的势。我们有以下熵的基本性质，其中性质(2)常被称为最大熵原理：

熵的基本性质：
(1) $H(X)\ge 0$;
(2) $H(X)\le \log |X|$，等号成立的条件是对X的所有取值x都有$P(X=x)=\frac{1}{|X|}$

证明：
(1)根据熵的定义，$H(X)\ge 0$显然成立。
(2)log为上凹函数，根据Jensen不等式有：
$$\begin{array}{rl}H(X)& =\sum _{X}P(X)\log \frac{1}{P(X)}\\ & \le \log \sum _{X}P(X)\frac{1}{P(X)}\\ & =\log |X|\end{array}$$
命题得证。

1.1.3 联合熵、条件熵、互信息

联合熵是基于联合概率分布对熵的推广。两个离散随机变量X和Y的联合熵定义为：
$$\begin{array}{rl}H(X,Y)& =E_{P(X,Y)}\left[\log \frac{1}{P(X,Y)}\right]\\ & =-\sum _{X,Y}P(X,Y)\log P(X,Y)\end{array}\text{\hspace{1em}(2)}$$
条件熵是基于条件概率分布对熵的推广。随机变量X的熵时用它的概率分布P(X)来定义的。如果知道另一个随机变量Y的取值为y，那么X的条件分布即为P(X|Y=y)。利用此条件分布可定义给定Y=y时X的条件熵：
$$\begin{array}{rl}H(X|Y=y)& =E_{P(X|Y=y)}\left[\log \frac{1}{P(X|Y=y)}\right]\\ & =-\sum _{X}P(X|Y=y)\log P(X|Y=y)\end{array}\text{\hspace{1em}(3)}$$
熵H(X)度量的是随机变量X的不确定性，条件熵H(X|Y=y)度量的则是已知Y=y后，X的不确定性。
上式(3)中，当y变化时，H(X|Y=y)也会发生改变，当知道Y的概率分布后，可以计算X关于Y的条件熵的期望值：
$$\begin{array}{rl}H(X|Y)& =\sum _{y\in {\Omega }_Y}P(Y=y)H(X|Y=y)\\ & =-\sum _{y\in {\Omega }_Y}P(Y=y)\sum _{X}P(X|Y=y)\log P(X|Y=y)\\ & =-\sum _Y\sum _{X}P(Y)P(X|Y)\log P(X|Y)\\ & =-\sum _{X,Y}P(X,Y)\log P(X|Y)\end{array}\text{\hspace{1em}(4)}$$
H(X|Y)称为给定Y时X的条件熵。
注意：H(X|Y)和H(X|Y=y)不一样，后者是已知Y取某一特定值时X的条件熵，即已知Y=y后，X剩余的不确定性。而前者时在未知Y的取值时，对观测到Y的取值后X剩余的不确定性的期望值。尤其值得注意的是，H(X|Y=y)可能比H(X)大，即知道Y的某个具体取值后，有可能增大对X的不确定性。而H(X|Y)永远不会比H(X)大，即平均来说，知道Y不会增加X的不确定性。下面给出一个具体的例子加以比较：
设已知联合分布P(X,Y)及其边缘分布P(X)和P(Y)如下表所示：

	$x_1$	$x_2$	$P(Y)$
$y_1$	0	3/4	3/4
$y_2$	1/8	1/8	1/4
$P(X)$	1/8	7/8

从而可得出：
$$\begin{array}{rl}& H(X)=-\frac{1}{8}\log \frac{1}{8}-\frac{7}{8}\log \frac{7}{8}=0.544;\\ & H(X|Y=y_1)=-0\log 0-1\log 1=0;\\ & H(X|Y=y_2)=-\frac{1}{2}\log \frac{1}{2}-\frac{1}{2}\log \frac{1}{2}=1;\\ & H(X|Y)=\frac{3}{4}H(X|Y=y_1)+\frac{1}{4}H(X|Y=y_2)=0.25\end{array}$$
可以看到：观测到$Y=y_1$后，可使X的熵减小；观测到$Y=y_2$后，反而使X的熵增大；但平均而言，对Y的观测使X的熵减小。
由此，我们定义互信息量为：
$$I(X;Y)=H(X)-H(X|Y)$$
称为Y关于X的信息，表示Y中包含多少关于X的信息。很容易证明$I(X;Y)=I(Y;X)$，因此又称之为X和Y之间的互信息。

互信息的性质1：
$$I(X;Y)=I(Y;X)$$

证明：
$$\begin{array}{rl}I(X;Y)& =H(X)-H(X|Y)\\ & =-\sum _{X}P(X)\log P(X)+\sum _{X,Y}P(X,Y)\log P(X|Y)\\ & =-\sum _{X,Y}P(X,Y)\log P(X)+\sum _{X,Y}P(X,Y)\log P(X|Y)\\ & =\sum _{X,Y}P(X,Y)\log \frac{P(X|Y)}{P(X)}\\ & =\sum _{X,Y}P(X,Y)\log \frac{P(X,Y)}{P(X)P(Y)}\end{array}$$
同理可得：
$$I(Y;X)=\sum _{X,Y}P(X,Y)\log \frac{P(X,Y)}{P(X)P(Y)}$$
因此，$I(X;Y)=I(Y;X)$得证。

熵的链规则：
$$H(X,Y)=H(X)+H(Y|X)=H(Y)+H(X|Y)\text{\hspace{1em}(5)}$$

证明：
$$\begin{array}{rl}H(X,Y)& =-\sum _{X,Y}P(X,Y)\log P(X,Y)\\ & =-\sum _{X,Y}P(X,Y)\log P(X)-\sum _{X,Y}P(X,Y)\log P(Y|X)\\ & =-\sum _{X}P(X)\log P(X)-\sum _{X,Y}P(X,Y)\log P(Y|X)\\ & =H(X)+H(Y|X)\end{array}$$
同理可证$H(X,Y)=H(Y)+H(X|Y)$

互信息的性质2：
$$I(X,Y)=H(X)+H(Y)-H(X,Y)\text{\hspace{1em}(6)}$$

证明：
等式左边：
$$I(X,Y)=H(X)-H(X|Y)$$
等式右边：
$$\begin{array}{rl}H(X)+H(Y)-H(X,Y)& =H(X)+H(Y)-(H(Y)+H(X|Y))(熵的链规则)\\ & =H(X)-H(X|Y)\end{array}$$
从而等式成立。
联合熵、条件熵和互信息之间的关系，可用如下文氏图来表示它们之间的关系：

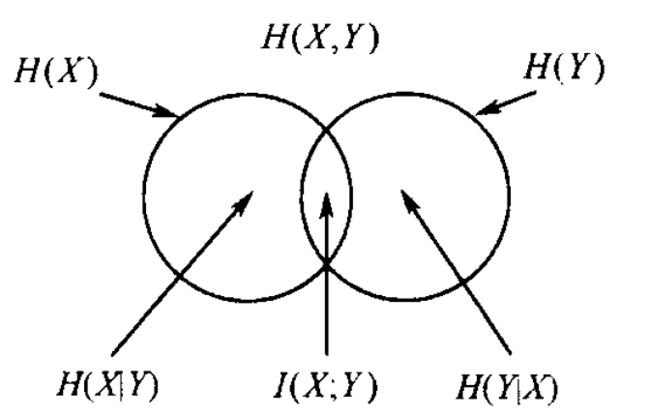
1.1.4 交叉熵和相对熵（KL散度）

在1.1.2节介绍熵的概念时，介绍了熵的期望编码长度的意义。交叉熵的概念也可以从期望编码长度的意义出发进行理解。
若信源X的理论概率分布为Q(X)，但其实际概率分布为P(X)，则使用理论概率分布构建的霍夫曼编码在实际概率分布下的期望编码长度即为交叉熵（Cross Entropy），定义为：
$$CEH(P,Q)=E_{P(X)}\left[\log \frac{1}{Q(X)}\right]=-\sum _{X}P(X)\log Q(X)$$
相对熵则定义为交叉熵与熵之差，即按照信源的理论概率分布Q设计的最优编码的期望码长会比按照实际概率分布P设计的最优编码的期望码长多几个比特。其定义如下：
$$KL(P,Q)=\sum _{X}P(X)\log \frac{P(X)}{Q(X)}$$
其中约定：$0\log \frac{0}{q}=0$；$\forall p>0:p\log \frac{p}{0}=\infty$.
KL(P,Q)又称为P(X)和Q(X)之间的Kullback-Leibler距离，或KL散度。但严格来讲，它并不是一个真正意义的距离，因为其不满足对称性。

信息不等式：
设P(X)和Q(X)为定义在随机变量X的状态空间${\Omega }_X$上的两个概率分布，则有：
$$KL(P,Q)\ge 0$$
其中，当且仅当P=Q，$\forall x\in {\Omega }_X$时等号成立。

证明：
$$\begin{array}{rl}KL(P,Q)& =\sum _{X}P(X)\log \frac{P(X)}{Q(X)}\\ & =-\sum _{X}P(X)\log \frac{Q(X)}{P(X)}\\ & \ge -\log \sum _{X}P(X)\frac{Q(X)}{P(X)}(根据下凸函数的Jensen不等式)\\ & =-\log \sum _{X}Q(X)\\ & =0\end{array}$$
信息不等式得证。
利用KL散度可以度量两个概率分布之间的差异。

1.1.5 互信息与变量独立

从1.1.3节给出的联合熵、条件熵与互信息之间关系的文氏图可以看出：对于随机变量X和Y，当互信息I(X,Y)=0时，X和Y相互独立；且$H(X|Y)\le H(X)$，等号也在X和Y独立时成立。我们也可以给出严格证明。
证明：
$$\begin{array}{rl}I(X,Y)& =\sum _{X,Y}P(X,Y)\log \frac{P(X,Y)}{P(X)P(Y)}(1.1.3节证明互信息性质1的中间结论)\\ & =KL(P(X,Y),P(x)P(Y))(KL散度的定义)\end{array}$$
由KL散度大于等于0可得：$I(X,Y)\ge 0$，当且仅当P(X,Y)=P(X)P(Y)时等号成立，即X与Y相互独立。
由于$I(X,Y)=H(X)-H(X|Y)\ge 0$，所以$H(X|Y)\le H(X)$，等号在X与Y相互独立时成立。
从信息论的角度，我们可以看出：两个随机变量相互独立等价于它们之间的互信息为0.
该结论还可以进一步推广到三个随机变量的情况。
对于随机变量X,Y,Z，条件熵H(X|Z)是给定Z时X剩余的不确定性，如果再进一步给定Y，X剩余的不确定性变为H(X|Z,Y)。这两者之差即为给定Z时观测Y的取值会带来的关于X的信息量，即给定Z时X和Y之间的条件互信息，定义如下：
$$I(X;Y|Z)=H(X|Z)-H(X|Z,Y)$$
类似上文证明$I(X;Y)=I(Y;X)$，我们也容易证明：
$$I(X;Y|Z)=I(Y;X|Z)$$
类似上文证明$I(X;Y)\ge 0$和$H(X|Y)\le H(X)$，我们也容易证明：
$$\begin{array}{rl}& I(X;Y|Z)\ge 0\\ & H(X|Y,Z)\le H(X|Z)\end{array}$$
其中等号仅在X与Y在给定Z时互相独立的情况下成立，记作$X\perp Y|Z$.
从信息论的角度，我们可以看出：给定Z时，两个随机变量X和Y相互条件独立等价于它们的条件互信息为0，即Y关于X的信息已全部包含在Z中，从而观测到Z后，再对Y进行观测不会带来关于X更多的信息。另一方面，如果X和Y在给定Z时相互不独立，则$H(X|Z,Y)<H(X|Z)$，即在已知Z的基础上对Y的进一步观测将会带来关于X的新信息，从而降低X的不确定性。