Learning Efficient Convolutional Networks through Network Slimming 论文学习

Abstract

由于计算资源消耗过高，在许多现实的应用上部署深度卷积网络就受到了限制。在这篇论文中，作者提出了一个新的CNN学习机制：1）降低模型的大小；2）降低运行时内存占用；3）减少计算操作的数量，而不会损失精度。作者通过一个简单但有效的方法，将网络的各个通道变得稀疏。和许多现有方法不同，此方法可以直接用在当前的CNN结构上，将训练过程中的额外开支降到最低，最终的模型也不需要任何特殊的软件或硬件来充当加速器。作者将此方法称作“网络裁剪”，它将大网络作为输入模型，在训练过程中，它会自动识别不重要的通道，并将之裁剪掉，这样输出的模型就会很小，而准确率相似。作者在多个SOTA CNN 模型（包括 VGGNet、ResNet、DenseNet等）上进行了裁剪，非常有效。对于 VGGNet，网络裁剪后，模型大小降低了20多倍，计算量降低了5倍多。

1. Introduction

近些年，CNN在计算机视觉任务上成为了主流方法，如图像分类、目标检测、语义分割等。大规模数据集、高端的GPU以及新的网络结构使得网络模型越来越大。例如，从 AlexNet，VGGNet 、GoogleNet 到 ResNet，ImageNet 分类挑战赛的冠军模型已经从8层网络演变到了100多层。

CNN 越大，虽然其表现能力会越强，但是也更消耗资源。例如，若输入图像分辨率为 $224\times 224$，152层的ResNet 就会有超过6000万个参数，需要200亿次的浮点计算。这对于移动端、穿戴设备来说想都不要想。

在实际应用中部署CNN受以下条件制约：1）模型大小：数以百万计的参数造就了 CNN强大的表现能力。这些参数，以及模型的结构信息，需要存储在磁盘上，在推理时被加载入内存中。比如，存储一个ImageNet 上常见的CNN模型需要至少300MB的空间，这对嵌入式设备来说太沉重了。2) 运行时内存：在推理时，CNN中间的激活与响应所消耗的内存空间甚至要比模型参数的存储还要大，即便 batch 大小为1。3)计算操作的数量：在高分辨率图像上，卷积操作对算力的消耗更加严峻。在移动设备上，一个较大的CNN模型可能要花费数分钟的时间来处理一张图片，这对实际应用是无法接受的。

人们提出了很多方法来压缩大型卷积网络，或直接学习一个更有效的CNN模型，用于快速推理。这些方法包括低秩近似、网络量化与二元化、权重剪枝、动态推理等。但是，这些方法只能解决上述一个或两个挑战。而且，部分方法需要特别设计的软件或硬件来进行加速。

另一个降低CNN资源消耗的方向就是网络稀疏化。我们可以在不同的网络层级上进行稀疏化，实现非常显著的压缩效果以及推理速度。但是这些方法通常需要特别的硬件或软件加速器的支持，尽管这要比非结构化的稀疏权重矩阵要容易些。

本文提出了一个简单而有效的训练机制 — 网络裁剪，它可以解决前面提到的挑战，在有限的资源下也可以部署大型CNN。本文的方法对 BN 层的缩放因子进行 L1 正则化，因而实现起来很简单，且不会对现有的CNN结构做额外的变动。通过 L1 正则化将 BN 层缩放因子的值变为0，使我们可以识别出那些不重要的通道（或神经元），因为每个缩放因子都对应着一个卷积通道（或全连接层中的神经元）。这就使我们接下来可以进行通道剪枝。该额外的正则项几乎不会损害模型性能。实际上，在一些案例中，它反而能提升模型的泛化能力。把不重要的通道裁剪掉，可能在短时间内会降低模型的表现，但我们可以对剪枝后的网络进行模型微调来补偿。剪枝后，网络的大小、运行时内存消耗以及计算操作个数会降低许多。我们可以多次重复上述步骤，最终得到一个 multi-pass 的网络裁剪方案，输出更紧凑小巧的网络。

作者在多个基准数据集和网络结构上进行实验，此方法可以将CNN模型的大小缩小20多倍，浮点运算数量降低5倍多，而精度不变甚至要更高。而且，本文的方法只用了传统的硬件和深度学习框架，不需要用任何稀疏存储格式或计算操作。

2. Related Work

这一节中，作者从五个方面讨论相关的工作。

低秩分解 就是在神经网络中通过奇异值分解（SVD）等方法来近似一个低秩矩阵。这个方法对全连接层特别管用，可以将模型的大小缩小约3倍，但是却不会带来任何明显的加速，这是因为CNN绝大多数操作都来自于卷积层。

权重量化。HashNet 提出了量化网络权重的方法。在训练之前，将网络的权重进行哈希化，分为不同的组，然后在每组内，权重值是共享的。这样，我们只需存储共享的权重和哈希索引，就可以节省大量的存储空间。[12] 使用了一个改进版的量化方法，将 AlexNet 和 VGGNet 压缩了35到49倍。但是，这些方法不会节约任何的运行时内存占用或推理时间，因为在推理时，我们需要将这些共享参数还原至原来的位置。

[28, 6] 将实数权重值量化为二进制或三进制权重（权重值仅为$\{-1,1\}$或$\{-1,0,1\}$）。由于我们只有按位(bitwise)操作，极大地降低了模型大小，并可以取得速度的显著提升。但是，这种 low-bit 近似方法通常会造成一些准确率损失。

权重裁剪/稀疏化。[12] 提出了在网络中，用较小的权重来裁剪那些不重要的网络连接。裁剪后的网络权重大部分都是0，因此我们就能以稀疏的格式来存储模型，降低存储空间。但是，该方法必须要用到特殊的稀疏矩阵库或硬件支持才能实现加速。而且，运行时内存占用的节省也非常有限，因为激活函数映射消耗了绝大多数的内存空间，而非权重。

论文 [12] ，在训练过程中并没有任何针对稀疏的指导意见。[32] 利用额外的 gates 变量对每个权重进行稀疏化约束，通过0 gate 值来裁剪网络连接，取得了较高的压缩率。该方法取得的压缩率要好于[12]，但是缺陷是一样的。

结构化裁剪/稀疏化。最近，[23] 提出了在CNN中用小权重来裁剪通道，然后再微调来提升准确率。[2] 在训练之前，对各通道间的连接进行随机失效处理，以此带来稀疏性，网络模型要小一些，但是也会造成一部分精度的损失。与这些方法相比，本文方法在训练过程中对各通道进行稀疏化，通道裁剪要更加平滑，精度损失要小得多。

[37] 在训练过中进行神经元级别的稀疏化，因此一些神经元可能会被裁剪掉。[35] 提出了结构化稀疏性学习（SSL）方法，对CNN结构的不同级别（滤波器、通道或层）进行稀疏化。这些方法在训练过程中都利用了分组稀疏正则化（group sparsity regularization）操作，来实现结构化的稀疏。本文方法并没有借助分组稀疏操作，而是对各通道的缩放因子进行简单的 L1 稀疏化，因而实现起来更简单。

因为这些方法只对网络结构的部分（如神经元、通道）进行裁剪或稀疏化，而非网络的权重，所以它们通常不需要什么特别的库（进行稀疏运算）来加快推理速度、节约运行时内存。本文的网络裁剪方法也属于这一类，无需特殊的库来实现。

神经结构学习。尽管SOTA 的CNN 通常是由专家设计的，目前也有一些在自动网络结构学习上的探索。[20] 提出了在给定资源预算的前提下，进行网络结构搜索的优化方法。[38, 1] 提出了用增强学习的方法来自动地学习神经网络结构。这些方法的搜索空间都非常大，因此我们需要训练上百个模型来分辨好模型和坏模型。本文的网络裁剪方法也可以看作为一个网络结构学习的方法，尽管其选择的余地只局限于每层的宽度内。但是，和前面的方法不同，网络裁剪仅需训练一次，就可以学习网络结构，这和我们对效率的追求是一致的。

3. 网络裁剪

本文目的是提供一个实现CNN通道稀疏化的简单方法。这一节中，作者首先探讨了通道稀疏化的好处和挑战，然后讨论了如何利用 BN 中的缩放因子来高效地识别不重要的通道，并对之进行裁剪。

通道稀疏化的优势。如[35,23,11]中所述，我们可以在不同的级别上实现稀疏化，如权重级别、卷积核级别、通道级别或网络层级别。细粒度级别越高（如权重级别），稀疏化越能给我们带来更高的灵活度和泛化能力，压缩率也会更高，但是这通常需要特殊的软件或硬件支撑，来在稀疏化的模型上进行快速推理。相反，细粒度越低（如网络层级别）就不需要特殊的库来实现加速，尽管它可能灵活性上差一些，因为有些层一整层都会被裁剪掉。事实上，移除掉某一层仅当网络很深时才有效，比如超过50层。然而，通道级别的稀疏化就在灵活度和实现难度上提供了一个平衡方案。它可以应用在任一CNN或全连接网络上（将每个神经元看作为一个通道），这样裁剪后的网络就可以看作为原网络的一个“减肥”后的版本，在常用的深度学习框架上就可以进行高效率的推理。

挑战。实现各通道的稀疏化需要对一个通道所有的连接进行裁剪。这就使得直接在预训练模型上裁剪权重没用，因为一个通道的输入端和输出端不太可能都是接近0的值。如[23]里所说的，在预训练的 ResNet 上进行通道裁剪，在不损失精度的前提下，只能降低约$10\%$的参数量。[35] 通过在训练过程中加入稀疏正则化解决了这个问题。特别地，他们在训练时采用了分组 LASSO 方法，将所有对应通道滤波器的权重缩小为0。但是，该方法需要计算正则项对于所有滤波器权重的梯度，这并不轻松。作者提出了一个非常简单的办法来解决上述挑战，具体细节如下。

缩放因子与激励稀疏的惩罚。本文的想法就是对每个通道都引入一个缩放因子$\gamma$，该因子与其对应通道的输出相乘。然后我们一起训练网络权重和缩放因子，并对后者进行稀疏归一化。最后，我们对那些因子值较小的通道进行裁剪，并对裁剪后的网络进行微调。本方法训练的目标函数为：

$$L=\sum _{(x,y)}l(f(x,W),y)+\lambda \sum _{\gamma \in \mathrm{T}}g(\gamma )$$

其中$(x,y)$表示训练的输入和真值，$W$表示训练权重，第一项对应着CNN的训练损失，$g(\cdot )$ 是对缩放因子进行的稀疏化惩罚，$\lambda$ 用于平衡前后项。在实验中，作者令$g(s)=|s|$，就是 L1-范数，用于获取稀疏性。作者使用次梯度下降作为non-smooth L1 惩罚项的优化方法。我们也可以将 L1 惩罚替换为 smooth L1 惩罚，这样在non-smooth 点就可避免使用次梯度。

由于裁剪一个通道基本上就是将它所有的输入和输出连接给去掉，我们就可以将网络变窄（如图1），而无需借助任何特殊的稀疏计算库。缩放因子就是帮我们进行通道选取的媒介。由于缩放因子是和网络权重一起优化的，网络就能自动地识别不重要的通道，并将之安全地移除而不会造成精度损失。

在BN层中使用缩放因子。批归一化（BN）在目前的CNN中广泛应用，可以提升收敛的速度与泛化能力。BN 对激活值进行归一化，这启发了我们将各通道的缩放因子利用起来，设计了一个简单而有效的方法。BN 层使用 mini-batch 的数据来对内部激活值进行归一化。设$z_{in}$和$z_{out}$为BN层的输入和输出，$B$表示当前的 mini-batch，BN 层进行如下的变换：

$$\hat{z}=\frac{z_{in}-{\mu }_B}{\sqrt{{\delta }_B^2+ϵ}};z_{out}=\gamma \hat{z}+\beta$$

${\mu }_B$和${\delta }_B$ 分别是$B$输入激活的平均值和标准方差，$\gamma$和$\beta$是仿射变换的参数（缩放和平移），可以将归一化后的值线性变换至任意的尺度。

在卷积层后插入一个带有通道缩放和平移参数的 BN 层是常见的操作。因此，我们可以直接将BN层的 $\gamma$ 参数作为缩放因子，用于网络裁剪。这样做的优势就是不会给网络带来额外的计算负担。事实上，对通道剪枝而言，这也可能是学习缩放因子最有效的方式。

1. 如果我们向一个没有 BN 层的 CNN 中加入 scaling 层，缩放因子的值是没法衡量一个通道重要性的，因为卷积层和 scaling 层都只是线性变换。卷积层的网络权重变大，缩放因子变小，可以得到一样的结果。

2. 如果我们在BN层之前加入 scaling 层，缩放层的作用就会被BN层的归一化操作完全抵消。

3. 如果我们在BN层之后插入 scaling 层，该通道就要面对连续两次的缩放操作。

通道裁剪与微调。在各通道内进行了激励稀疏的归一化之后，模型中许多缩放因子的值就变成了0（看图1）。然后我们就可以对缩放因子近似0的通道进行裁剪，去除其所有的连接和对应的权重。对于所有的层，我们通过一个全局阈值来裁剪通道，该阈值是根据所有缩放因子的值按照一定的比例设定的。例如，要裁剪掉$70\%$的低缩放因子，我们就将其百分比阈值设为$70\%$。这样之后，网络的参数和计算操作量就要少许多，并且节约运行时内存占用。

裁剪可能会造成一定的精度损失，尤其当裁剪比例较高时，但是我们可以通过随后的微调来弥补。在很多实验案例中，相较于原来未剪枝的模型，微调后的剪枝模型可以取得更高的精度。

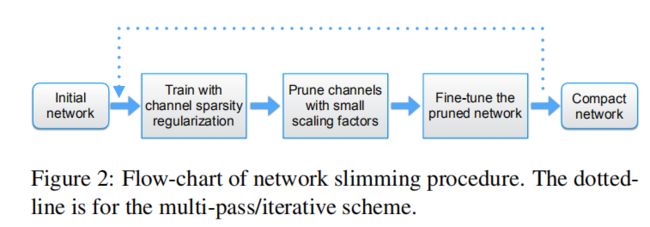
multi-pass 方案。我们也可以将之从 single pass（训练过程包括：稀疏正则化、剪枝、微调） 扩展到 multi-pass。裁剪后的网络会比较窄，我们可以多次地重复该过程，学习一个非常紧凑的模型。该流程如图2虚线部分所示。实验结果显示，multi-pass 方案可以取得更好的压缩效果。

处理跨层连接与pre-activation结构。上述网络裁剪过程可以应用在绝大多数的网络结构上，如 AlexNet、VGGNet。但是当我们将之应用在含有跨层连接与pre-activation的结构时，如 ResNet 和 DenseNet，我们就要对之进行一些改动。对于这些网络，某一层的输出可能是后续多个层的输入，这样BN层就会出现在卷积层之前。这种情况中，在这一层的输入端就存在稀疏性，即该层有选择地利用了部分通道。为了在测试时减少参数量和计算量，我们需要加入一个通道选择层来遮住那些识别出来的、不重要的通道。

4. 实验

Pls read paper for more details.